Let us consider the polarization evolution along the wave trajectory in the magnetospheric plasma. Such a problem has already been studied in application to polarization-limiting effect (Lyubarskii & Petrova 1999; Petrova & Lyubarskii 2000). In that case the plasma was supposed to be embedded in an infinitely strong magnetic field. Indeed, well within the magnetosphere the magnetic field strength is so high that the critical angle for the circularly polarized natural modes is too small. So in general the wave propagation is quasi-transverse with respect to the magnetic field, i.e. the non-coupled natural waves are linearly polarized. Then for the polarization evolution there is no essential distinction between whether the magnetic field strength is regarded as finite or infinite.
In the region of quasi-longitudinal propagation, polarization of the natural modes can differ essentially becoming almost circular. Although this region is rather narrow, it is of a particular interest for the present consideration, since it is the region where the conversion of waves is expected to occur. So it is reasonable to take into account both the finiteness of the magnetic field strength and the difference in the distribution functions of the plasma constituents.
Note that the region of conversion lies at distances
![]() (see
below), in which case we can ignore the magnetosphere rotation. As was found
earlier (Petrova & Lyubarskii 2000), the corrections allowing for the
rotational aberration are not significant even in the polarization-limiting
region, though it is situated much higher.
(see
below), in which case we can ignore the magnetosphere rotation. As was found
earlier (Petrova & Lyubarskii 2000), the corrections allowing for the
rotational aberration are not significant even in the polarization-limiting
region, though it is situated much higher.
The wave fields ![]() and
and ![]() are described by the Maxwell's
equations:
are described by the Maxwell's
equations:
| (1) | |||
| (2) | |||
| (3) |
![\begin{eqnarray*}{\vec j}_{\alpha}\equiv q_{\alpha}[n_{\alpha}{\vec v}_{0\alpha}+n_{0\alpha}
{\vec v}_{\alpha}],
\end{eqnarray*}](/articles/aa/full/2001/42/aa1063/img26.gif)
The equation of the particle motion in the external magnetic field of the
strength
![]() is written as follows:
is written as follows:
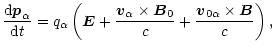 |
(4) |
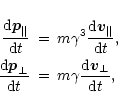
The tracing of the polarization evolution of the waves starts from the region
where refraction is already inefficient (i.e., ![]() ,
where n is the
refractive index of the ordinary superluminous waves; the extraordinary waves
are not subject to refraction at all). At the same time, in this region the
difference between the refractive indices of the waves still should be high
enough to prevent the mode coupling:
,
where n is the
refractive index of the ordinary superluminous waves; the extraordinary waves
are not subject to refraction at all). At the same time, in this region the
difference between the refractive indices of the waves still should be high
enough to prevent the mode coupling:
![]() .
Then
the geometrical optics approximation is valid and the wave behaviour is well
known: the polarization plane follows the orientation of the ambient
magnetic field.
.
Then
the geometrical optics approximation is valid and the wave behaviour is well
known: the polarization plane follows the orientation of the ambient
magnetic field.
Seeing that the waves propagate along straight lines, one can choose a
three-dimensional Cartesian coordinate system with the z-axis along the wave
trajectory. So all the quantities in Eqs. (1)-(4) depend only on the
z-coordinate. Moreover, further simplification is possible. The wave modes
propagating in opposite directions do not interact with each other given
that the refractive indices are far from zero (i.e. in the absence of
reflections). Hence, we shall treat only the waves propagating in the positive
direction of the z-axis. Since the refractive indices of the waves considered are
very close to unity, the spatial dependence of the wave electric field can
be presented as follows:
| (5) |
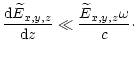 |
(6) |
Keeping in mind the above considerations and using Eq. (2) one can write the
component equations for the equation of motion (4) as follows:
| (7) |
| = | ![$\displaystyle \frac{q_\alpha^2B_0\left [E_yb_z{-}\beta_{0\alpha}E_xb_xb_y{-}
\b...
...y(b_y^2{+}b_z^2){-}E_zb_y\right ]}{m^2c(\omega_{\rm H}^2{-}\omega^
{\prime 2})}$](/articles/aa/full/2001/42/aa1063/img55.gif) |
||
| + | ![$\displaystyle \frac{iq_\alpha\omega^\prime}{m(\omega_{\rm H}^2-\omega^{\prime^2...
...pha b_x[E_xb_x+E_yb_y+E_zb_z]}{m\gamma_\alpha^3\omega (1-
\beta_{0\alpha}b_z)},$](/articles/aa/full/2001/42/aa1063/img56.gif) |
||
| = | ![$\displaystyle \frac{q_\alpha^2B_0\left [E_x(\beta_{0\alpha} (b_x^2{+}b_z^2){-}b...
...\alpha}E_yb_xb_y{+}b_xE_z\right ]}{m^2c(\omega_{\rm H}^2{-}\omega^
{\prime 2})}$](/articles/aa/full/2001/42/aa1063/img58.gif) |
||
| + | ![$\displaystyle \frac{iq_\alpha\omega^\prime}{m(\omega_{\rm H}^2-\omega^{\prime^2...
...pha b_x[E_xb_x+E_yb_y+E_zb_z]}{m\gamma_\alpha^3\omega (1-
\beta_{0\alpha}b_z)},$](/articles/aa/full/2001/42/aa1063/img56.gif) |
||
| = | ![$\displaystyle \frac{iq_\alpha b_z[E_xb_x+E_yb_y+E_zb_z]}{m\gamma_\alpha^3\omega...
...yb_x-E_xb_y)(1-\beta_{0\alpha}b_z)}
{m^2c(\omega_{\rm H}^2-\omega^{\prime 2})},$](/articles/aa/full/2001/42/aa1063/img60.gif) |
(8) |
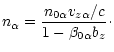 |
(9) |
![$\displaystyle \frac{{\rm d}E_x}{{\rm d}z}{+}\frac{2\pi}{c}\sum_\alpha \frac{q_\...
...a}b_z}[v_{x\alpha}(1{-}\beta_{0\alpha}b_z){-}v_{z\alpha}
\beta_{0\alpha}b_x]=0,$](/articles/aa/full/2001/42/aa1063/img64.gif) |
(10) |
![$\displaystyle \frac{{\rm d}E_y}{{\rm d}z}{+}\frac{2\pi}{c}\sum_\alpha \frac{q_\...
...a}b_z}[v_{y\alpha}(1{-}\beta_{0\alpha}b_z){+}v_{z\alpha}\beta_{0\alpha}
b_y]=0,$](/articles/aa/full/2001/42/aa1063/img65.gif) |
|
| Ez+ |
Ez=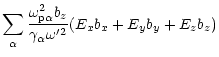 |
|
![$\displaystyle {+}\sum_\alpha \frac{\omega_{\rm p\alpha}^2\gamma_\alpha}{\omega_...
...mega^{\prime
2}}[(E_xb_x{+}E_yb_y)(b_z{-}\beta_{0\alpha}){-}E_z(b_x^2{+}b_y^2)]$](/articles/aa/full/2001/42/aa1063/img68.gif) |
|
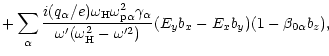 |
(11) |
| (12) |
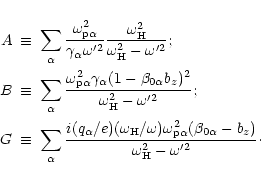
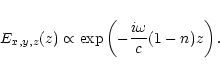
Copyright ESO 2001