1 Introduction

1.1 Observational evidence for orthogonally polarized modes

Pulsar radio emission usually shows a high percentage of linear polarization, with the position angle changing across the pulse. A smooth monotonic variation of the position angle with pulse longitude can be explained within the framework of a well-known rotating-vector model (Radhakrishnan & Cooke 1969): the vector of the local magnetic field at the emission region, which is thought to determine the orientation of the polarization plane of pulsar radiation, changes its projection onto the plane of the sky as the pulsar rotates. The resultant S-shaped swing of the position angle is indeed consistent with that observed for many pulsars. However, in a number of cases this smooth swing is broken by abrupt, approximately $90^\circ$ transitions in position angle (e.g., Manchester et al. 1975). The single-pulse observations have demonstrated that for each of the orthogonal modes the position angle variations roughly follow the predictions of the rotating-vector model (Backer et al. 1976), while the switching between the modes is a stochastic process (Cordes et al. 1978).

The comprehensive observational data (Manchester et al. 1975; Cordes et al. 1978; Backer & Rankin 1980; Stinebring et al. 1984a,b) have proved that the phenomenon of orthogonal polarization modes (OPMs) is a fundamental property of pulsar radiation. It is observed for almost all pulsars (of those subjected to detailed polarization studies) and takes place over the whole range of pulse longitudes, with the frequency of mode occurence varying considerably over a pulse. The OPM-phenomenon can be observed over a broad frequency range (from 100 MHz Suleymanova & Pugachev 2000 to 10 GHz Xilouris et al. 1995) and it appears to be strongly coupled to the intensity variations at all time scales, from micropulses and subpulses (Cordes & Hankins 1977) to single pulses (Cordes et al. 1978) and mode-changing average intensity profiles (Rankin 1988). The observed $90^\circ$-jumps of the position angle of linear polarization are found to be accompanied by a sense reversal in circular polarization (Cordes et al. 1978), so that the transitions between the polarization states are purely orthogonal. At higher frequencies both modes seem to become comparable in intensity and frequency of mode occurence for most of the pulse, causing a marked depolarization in average profiles (Manchester et al. 1975).

Despite the apparent progress in studying the main features of OPMs, to date there is no commonly accepted interpretation of this phenomenon. Moreover, the very question whether the OPMs are disjoint or superimposed still remains open. Indeed, the observational data yield no direct evidence whether at any instant only one OPM is active or whether both modes occur simultaneously, with the resultant position angle being that of the dominant mode. The first attempts to construct mode-separated profiles of the observed pulsars were based on the assumption of disjoint OPMs (Cordes et al. 1978; Rankin 1988; Gil et al. 1991; Gil et al. 1992). Recently the technique for calculating the mode profiles was developed for the model of superposed OPMs (McKinnon & Stinebring 1998, 2000). Both these methods provide convenient representation of the observational data. However, the assumptions of disjoint and superimposed modes lead to essentially distinct mode-separated profiles, so that the question arises regarding what the true polarization properties of OPMs are. Apparently, to choose between the disjoint and superimposed models one should have a notion of the underlying mechanism of generation of OPMs.

1.2 Earlier theoretical approaches

Since the discovery of OPMs in pulsar radiation (Manchester et al. 1975) numerous ideas were put forward to explain this phenomenon. In some theories the mode switching is supposed to be intrinsic to the radio emission mechanism (e.g., Gangadhara 1997). In this way, however, one faces another global problem: the emission mechanism itself is still obscure. The only undoubted factor is that pulsar radio emission is a result of some processes in the magnetospheric plasma streaming along the open magnetic field lines. Narrowness and stability of the observed pulses imply that the radio emission originates well within the magnetosphere. It is important that the process of radio emission adjusts to the presence of the magnetospheric plasma: whatever the emission mechanism it can produce only the natural waves of the ambient plasma. It should be mentioned that the disjoint OPMs constructed on the basis of the observational data cannot be intrinsic to the emission mechanism, since the natural waves are, by definition, completely polarized, whereas the disjoint modes usually show partial polarization. Within the framework of superimposed OPMs, two natural waves should be produced independently (to provide an incoherent mixture of radiation with two polarization states), but at the same time the efficiencies of the two mechanisms should vary in a way so as to account for the complex picture of the observed OPM-transitions as well as the high-frequency depolarization of pulsar radiation.

In a number of theories the orthogonal transitions in pulsar polarization are regarded as a consequence of the propagation effects. The first theories have related the OPM-phenomenon to the cyclotron absorption (Manchester et al. 1975) or induced scattering (Blandford & Scharlemann 1976) occasionally preferential for one of the modes. The early studies of the natural waves in pulsar plasma have led to a new view of the nature of OPM-transitions (Melrose 1979; Allen & Melrose 1982). The natural waves appear to be linearly polarized in orthogonal planes. Having different refractive indices, they become separated in space and in angle during their propagation through the plasma, with the value of the separation being strongly dependent on the conditions in the ambient plasma. This separation was suggested to underlie the observed transitions between OPMs.

Further investigation of the dispersive properties of pulsar plasma (e.g., Arons & Barnard 1986) gave rise to a more rigorous numerical treatment of refraction (Barnard & Arons 1986). The resultant knowledge of the features of wave behaviour in the magnetospheric plasma became a corner-stone of the comprehensive qualitative picture of the OPM-phenomenon developed by McKinnon (1997) (see also von Hoensbroech et al. 1998; von Hoensbroech 1999).

An ultrarelativistic highly magnetized plasma allows three natural waves. One of them, the extraordinary one, has a vacuum dispersion law and therefore propagates without refraction. Given the oblique propagation with respect to the magnetic field, one branch of the dispersion curve corresponding to ordinary waves is completely subluminous, while the other is completely superluminous. The subluminous waves are found to be "ducted'' along the magnetic field lines (Barnard & Arons 1986). Given that the waves in a broad frequency range originate at approximately the same altitude in the open field line tube, the lower the frequency - the stronger refraction. So at low enough frequencies the ordinary subluminous mode is well separated from the extraordinary mode due to efficient refraction, whereas at higher frequencies they overlap.

Supposing that these modes are generated by independent mechanisms and compete in intensity one can explain the occasional transitions between the orthogonal polarization states as well as the high-frequency depolarization of pulsar radio emission. However, one cannot but mention that the extraordinary mode (being characterized by the vacuum dispersion law) is not generated by any common processes in the plasma; at the same time, the ordinary subluminous wave (being easily generated, e.g., by the plasma instabilities) experiences severe Landau damping and therefore does not escape directly from the magnetosphere. Note that linear coupling of the subluminous mode to the superluminous one is inefficient at pulsar conditions (Bliokh & Lyubarskii 1996).

1.3 Working model

As shown by Lyubarskii (1996), the subluminous waves suffer intense induced scattering off the plasma particles. As a result, the waves become superluminous, with the frequencies being of the order of the local Lorentz-shifted proper plasma frequency:

$$\begin{eqnarray*}\omega\sim\omega_{\rm p}\sqrt{\gamma}, \end{eqnarray*}$$

where $\omega_{\rm p}$ is the customary plasma frequency, $\gamma$ the plasma Lorentz-factor.

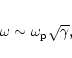
The investigation of refraction was extended to the ordinary superluminous waves originating at the characteristic plasma frequencies (Lyubarskii & Petrova 1998; Petrova & Lyubarskii 2000; Petrova 2000). It was found that in this case refraction is determined mainly by the gradient of the plasma number density across the open field line tube. According to standard models (e.g., Arons & Scharlemann 1979), the plasma number density decreases toward both the magnetic axis and tube edges. It is obvious that in the course of refraction a ray diverges from its initial orientation in the direction of the plasma density decrease. So the rays originating in the inner part of the tube bend toward the magnetic axis, whereas those emitted in the outer part of the tube deviate outwards. If refraction is strong enough, the rays emitted in the inner part of the tube can intersect the magnetic axis and come into the opposite half of the tube, where they start to deviate in the opposite direction because of oppositely directed transverse density gradient. Since in our consideration the waves are supposed to originate at the local characteristic plasma frequency (i.e. a sort of radius-to-frequency mapping), refraction appears to become more intense at higher frequencies (e.g., Lyubarskii & Petrova 1998), contrary to the conclusion of Barnard & Arons (1986). These basic features of ray behaviour in pulsar plasma proved to have a number of observational consequences. It was shown that refraction not only influences the pulse width and its frequency dependence (Lyubarskii & Petrova 1998), but also modifies the profile shape, giving rise to ray grouping into separate components (Petrova & Lyubarskii 2000; Petrova 2000).

Note that refraction is significant only at distances of the order of the emission altitude, $r\sim r_{\rm e}$, since the plasma number density rapidly decreases with the distance. Further on the waves propagate along straight lines. It should be pointed out that at $r\sim r_{\rm e}$ the scale length for beatings between the non-damping natural modes, $L_{\rm b}$, is much less than the characteristic scale length for change in the plasma parameters, L. Therefore the modes do not interact with each other and their polarization evolution can be described in terms of geometrical optics. The primordial ordinary waves considered in our model remain polarized in the same plane as the wave vector and external magnetic field, the polarization plane being slowly rotating along the trajectory due to change in the orientation of the ambient magnetic field. As soon as the plasma number density decreases considerably, $L_{\rm b}$ matches L; then geometrical optics fail, the polarization plane no longer follows the local orientation of the magnetic field and wave mode coupling holds. As a result, the wave polarization becomes elliptical, with the polarization ellipse rotating along the trajectory. After the plasma density becomes negligible, the waves preserve their polarization state. This is a so-called polarization-limiting effect (Cheng & Ruderman 1979; Stinebring 1982; Barnard 1986; Petrova & Lyubarskii 2000). It is found to be responsible for the partial circular polarization often observed in pulsar radiation.

1.4 Statement of the problem

The present paper is devoted to further investigation of pulsar polarization. Namely, it suggests the explanation of the OPM phenomenon which arises naturally within the framework of the above model of wave propagation in the magnetospheric plasma: the presence of the two OPMs is attributed to the linear conversion of waves in the region of quasi-longitudinal propagation with respect to the magnetic field. Note that the possibility of the non-linear conversion of the waves in pulsar plasma has already been considered by Lyutikov (1999). Here we concentrate purely on the linear effects.

It is known that at the conditions relevant to pulsar plasma the wave propagation is generally quasi-transverse. However, according to numerical ray tracings (e.g., Lyubarskii & Petrova 1998; Petrova 2000), it is a common situation that the rays which have suffered refraction (in either an outward or inward direction) further on pass through the region, where the wave vector is nearly aligned with the ambient magnetic field. Indeed, the outward ray deviation is later on compensated for by the magnetic line divergence. The same happens for the inner rays which have intersected the magnetic axis in the course of refraction.

In the region of quasi-longitudinal propagation the refractive indices of the non-damping natural waves become essentially close to each other, so that geometrical optics breaks and linear coupling holds. As a result, the energy can be partially transmitted into the other (extraordinary) mode. It is shown that at the reasonable conditions in pulsar plasma the ordinary wave can be almost completely transformed into the extraordinary one. Out of the region of conversion the resultant waves propagate independently (geometrical optics is again valid until they reach the polarization-limiting region). It will be shown that as a result of the polarization-limiting effect the polarization of both types of waves becomes elliptical, with the sense being opposite and the position angle being shifted in such a way that the modes remain orthogonal.

Whether one mode or another is dominant depends on the conditions in the region of conversion, which are expected to suffer temporal variations. Furthermore, changes in the plasma density distribution can affect refraction, so that for a fixed ray the regime of quasi-longitudinal propagation arises or does not arise. (An idea of temporal variations in the plasma distribution is supported by the fact that pulsar profiles are only stable on average.)

Since at higher frequencies refraction becomes more prominent, the possibility of longitudinal propagation is met for most of the rays, so that the resultant OPM-transitions can lead to significant depolarization of the observed emission. Thus, the linear conversion of the primordial ordinary superluminous waves can really account for the main features of the observed OPM-phenomenon.

The present paper is arranged as follows. In Sect. 2 we derive the equations describing polarization evolution in an ultrarelativistic magnetized plasma taking into account finiteness of the magnetic field strength. Linear conversion of the natural modes of pulsar plasma is considered in Sect. 3. Wave propagation in the polarization-limiting region is also examined there. In Sect. 4 we compare the consequences of our theory with the observed features of the OPM-phenomenon. The results are summarized in Sect. 5.