SimLine solves the line radiative transfer problem discussed
in Appendix A.1 in a spherically symmetric configuration by means
of a ![]() -iteration. The code is similar to the concept described by
Dickel & Auer (1994) but it contains several extensions and achieves
a higher accuracy from an adaptive discretisation of all independent
quantities.
-iteration. The code is similar to the concept described by
Dickel & Auer (1994) but it contains several extensions and achieves
a higher accuracy from an adaptive discretisation of all independent
quantities.
SimLine integrates the radiative transfer Eq. (A.2)
for a number of rays numerically.
In spherical symmetry it is sufficient to consider the propagation
of radiation in one arbitrary direction which is taken as z here.
The integral is computed stepwise from zi-1 to zi
In spherical symmetry the spatial integration of the radiative energy
density (Eq. (B.12)) can be reduced to
With the values of the radiative energy density at each radial point and for
each transition, the system of balance equations can be solved
providing new level populations. Here, a LU decomposition algorithm
with iterative improvement (Press et al. 1992) is used. The new level populations
are used in the next iteration as input for the radiative transfer equation.
The whole ![]() -iteration scheme is
solved using the convergence accelerator introduced by Auer (1987).
-iteration scheme is
solved using the convergence accelerator introduced by Auer (1987).
Depending on the physical situation the initial guess is either the optically thin limit, thermalisation or the solution of the radiative transfer equation using the LVG approximation (Eq. (B.15)). The stability of the local radiation field is used as convergence criterion. The number of iterations required for convergence depends strongly on the optical depth of the model cloud. For the examples discussed in this paper only about a dozen iterations were necessary but other test cases with complex molecules like water, non-monotonic velocity gradients, and high optical depths require several hundred iterations.
The turbulence description uses two additional parameters for
each spatial point: the width of the velocity distribution
![]() providing the
local emission profile for optically thin lines and the correlation length
of the macroturbulent density or velocity distribution
providing the
local emission profile for optically thin lines and the correlation length
of the macroturbulent density or velocity distribution
![]() .
.
The width of the velocity distribution ![]() is composed of a
turbulent and a thermal contribution
is composed of a
turbulent and a thermal contribution
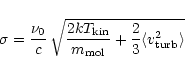 |
(B.3) |
For the local treatment of coherent units in a turbulent medium the
considered volume element is subdivided into numerous
clumps with a thermal internal velocity dispersion.
When each clump is characterized by a Gaussian density distribution
of molecules with about the same velocity
![]() the effective absorption coefficient at the considered
velocity for the whole medium is
the effective absorption coefficient at the considered
velocity for the whole medium is
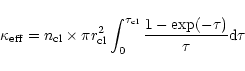 |
(B.4) |
When the turbulent velocity dispersion ![]() is at least three times
as large as the thermal velocity dispersion
is at least three times
as large as the thermal velocity dispersion
![]() ,
we obtain
an effective absorption coefficient
,
we obtain
an effective absorption coefficient
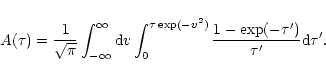 |
(B.6) |
To simulate the effect of a central continuum
source in the cloud, it is possible to assume an H II region in the cloud
centre.
The H II region is characterised by two parameters, the electron density
![]() and the kinetic electron temperature
and the kinetic electron temperature ![]() .
.
The absorption coefficient for electron-ion bremsstrahlung in the
Rayleigh-Jeans approximation is given by:
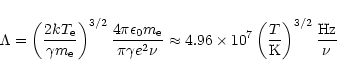 |
(B.8) |
For a thermal plasma, the emission coefficient follows
from the Planck function
When the level populations are known, the beam temperature relative
to the background is computed by the convolution of the emergent intensity
with the telescope beam.
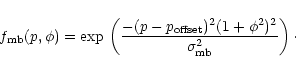 |
(B.11) |
The design of the code is directed towards a high accuracy of the computed line profiles. All errors in the different steps of the program are explicitly user controlled by setting thresholds. All discretisations necessary to treat the problem numerically are performed in an adaptive way, i.e. there is no predefined grid and all grid parameters will change during the iteration procedure. The system of balance equations is truncated whenever the excitation of all higher levels falls below a chosen accuracy limit.
Furthermore, the code was pushed towards a high flexibility, i.e. the ability to treat a very broad range of physical parameters with the same accuracy and without numerical limitations. The systematic velocities e.g. may range from 0 to several times the turbulent velocity and the optical depths may vary from negative values for weak masing to values of several thousands.
The program is not optimised towards a high speed. Other codes with lower inherent accuracy may easily run a factor 10 faster, and further improvements are possible. Nevertheless, the code is suitable for an interactive work even on a small PC with execution times of a few seconds for the models considered in this paper.
Copyright ESO 2001