The physical parameters of a cloud model and the
emerging line profiles and intensities are linked by the
radiative transfer problem. It relates the molecular emission
and absorption coefficient at one point to the
radiation field determined by the emission and transfer of
radiation at other locations in the cloud.
The quantity entering the balance equations for the level populations at
a point ![]() is the local radiative energy density u within
the frequency range for each transition:
is the local radiative energy density u within
the frequency range for each transition:
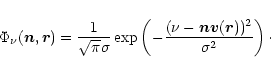 |
(A.3) |
For a molecular cloud this results in a huge system of integral equations interconnecting the level populations and intensities at all points within a cloud.
A simple way to avoid the nonlinear equation system is the escape
probability approximation that is widely applied to interpret
molecular line data.
It is based on the assumption that the excitation, and thus the
absorption and emission coefficients, are constant within
those parts of a cloud which are radiatively coupled.
Then the radiative transfer equation (Eq. (B.13)) can be
integrated analytically. We obtain for the integrated radiative
energy density:
| = | 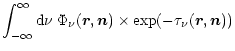 |
(A.5) | |
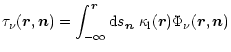 |
(A.6) |
There are two main concepts to define the interaction region and thus to
compute the escape probability. The first one is the large velocity
gradient approximation introduced by Sobolev (1957). Here,
the interaction region is determined by a velocity gradient in the cloud
that displaces the line profiles along the line of sight so that
distant regions are radiatively decoupled. When the resulting interaction
region is sufficiently small it is justified to assume constant parameters.
The escape probability then follows
We used another method, the static escape probability
model. It does not depend on the velocity structure but
assumes a special geometry of
the interaction region. Stutzki & Winnewisser (1985) solved the problem for
a homogenous spherical cloud with constant excitation parameters.
The resulting escape probability is taken to be constant
The surface brightness temperature towards the centre of the cloud is
given by the same expression as Eq. (A.9) when we use
the line integrated optical depth at the cloud centre
![]() instead of
instead of
![]() .
It decays with growing distance from the cloud
centre. Averaged over the whole cloud, the brightness temperature
at the line centre is given by
.
It decays with growing distance from the cloud
centre. Averaged over the whole cloud, the brightness temperature
at the line centre is given by
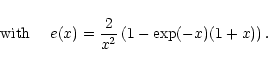
When the velocity gradient in the LVG approximation is computed from
the total line width and the cloud size, it turns out that both methods
agree when applied to observations with a small beam towards the cloud
centre. Only for large-beam observations, they differ in the functions
in Eqs. (A.9) and (B.22), which are either
![]() or
or ![]() ,
but result in similar values.
,
but result in similar values.
By setting up a table of beam temperatures from Eqs. (A.9)
and (B.22) and comparing the observed line intensities
with the tabulated values we can derive three parameters from the
observations: the kinetic
temperature
![]() and the gas density
and the gas density
![]() providing
mainly the source function, and the column density of the considered
molecules relative to the line width
providing
mainly the source function, and the column density of the considered
molecules relative to the line width
![]() providing the photon
escape probability.
providing the photon
escape probability.
Copyright ESO 2001