

Up: The effect of anisotropic
Subsections
In a plasma with a non-zero magnetic field, the motion of the particles along
the magnetic field lines differs fundamentally from their motion perpendicular
to the field lines. This points at the necessity of allowing different amounts
of random energy for particle motions parallel and perpendicular to the field,
respectively. One expects the distribution function to have an axial symmetry
around the local magnetic field 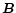 ,
if the Larmor radii of the
particles are very small compared to the density scale in the perpendicular
direction. Then the gas pressure is a tensor
,
if the Larmor radii of the
particles are very small compared to the density scale in the perpendicular
direction. Then the gas pressure is a tensor
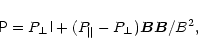 |
(2) |
where 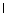 is the unit tensor. In a steady state, we can write all
the macroscopic conservation laws in form (e.g., Boyd & Sanderson 1969)
is the unit tensor. In a steady state, we can write all
the macroscopic conservation laws in form (e.g., Boyd & Sanderson 1969)
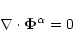 |
(3) |
where
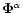 is one of the fluxes: the mass flux,
is one of the fluxes: the mass flux,
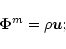 |
(4) |
the momentum flux,
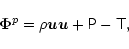 |
(5) |
with
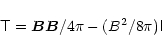 |
(6) |
giving the electromagnetic stress tensor (neglecting small electric-field contributions);
or energy flux
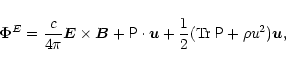 |
(7) |
which holds for a non-relativistic gas with zero heat flux. Here,
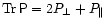 is the trace of the pressure tensor.
is the trace of the pressure tensor.
We consider the conservation laws across a planar shock discontinuity. In
addition to the macroscopic conservation laws, we use Maxwell's equations
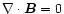 and
and
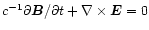 ,
and Ohm's law in form
,
and Ohm's law in form
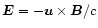 to
arrive at jump conditions (see also Lyu & Kan 1986)
to
arrive at jump conditions (see also Lyu & Kan 1986)
![$\displaystyle \left[ \left\{ \frac{\rho }{2}u_{n}^{2}+\frac{5P_{\parallel }}{2}...
... u_{n}-\phi B_{n}\frac{\vec{u}_{t}\cdot \vec{B}_{t}}{4\pi }\right] ^{2}_{1} = 0$](/articles/aa/full/2001/40/aah2708/img44.gif) |
|
|
(11) |
expressing the continuity of normal magnetic and tangential electric fields
across the shock (Eq. (8)), and the conservation of
mass and perpendicular momentum (Eq. (9)), parallel
momentum (Eq. (10)), and energy
(Eq. (11)). Here, subscripts n and t denote
vector components normal and tangential to the planar shock and
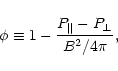 |
(12) |
is the firehose factor specifying the pressure anisotropies. Regarding the upstream
values for all variables as known input parameters and the downstream values
as unknowns, we have altogether 8 equations and 9 unknowns. To close the set,
we simply take the downstream pressure to be isotropic, which should be reasonable
at least for shocks with a compression ratio differing considerably from unity;
for such shocks the transition layer is likely to produce short-scale magnetic
turbulence that can lead to the isotropization of the particles just downstream
the shock.
Pressure anisotropies also modify the dispersion relation of Alfvén waves, which
at long-wave-length limit becomes (e.g., Stix 1962)
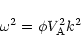 |
(13) |
for circularly polarized waves propagating parallel to the mean field. Here, the
wave frequency 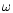 and the wavenumber k are measured in the plasma
frame. For positive values of
and the wavenumber k are measured in the plasma
frame. For positive values of 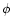 ,
Eq. (13)
describes waves propagating at phase speed
,
Eq. (13)
describes waves propagating at phase speed
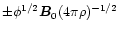 parallel (+) or anti-parallel (-) to the mean magnetic
field,
parallel (+) or anti-parallel (-) to the mean magnetic
field,
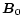 .
For negative values of
.
For negative values of 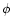 ,
Eq. (13) describes the firehose instability: the
magnetic fluctuations become group-standing and grow exponentially at rate
,
Eq. (13) describes the firehose instability: the
magnetic fluctuations become group-standing and grow exponentially at rate
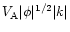 .
From now on we take
.
From now on we take
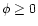 ,
although the
results could be generalized also to the firehose-unstable case. Note that the
firehose unstable case can only be realized for
,
although the
results could be generalized also to the firehose-unstable case. Note that the
firehose unstable case can only be realized for
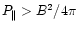 ,
so restricting the analysis to the stable cases is natural for plasmas with low
,
so restricting the analysis to the stable cases is natural for plasmas with low
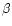 .
.
Combining Ohm's and Faraday's laws gives the relation
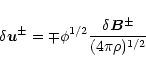 |
(14) |
between the velocity and magnetic-field perturbations associated with Alfvén
waves propagating parallel (+) or anti-parallel (-) to the mean
magnetic field. We assume that the turbulent magnetic field can be decomposed
to two wave fields propagating in opposite directions,
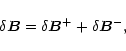 |
(15) |
yielding the equation
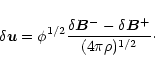 |
(16) |


Up: The effect of anisotropic
Copyright ESO 2001
![]() ,
if the Larmor radii of the
particles are very small compared to the density scale in the perpendicular
direction. Then the gas pressure is a tensor
,
if the Larmor radii of the
particles are very small compared to the density scale in the perpendicular
direction. Then the gas pressure is a tensor
![]() and
and
![]() ,
and Ohm's law in form
,
and Ohm's law in form
![]() to
arrive at jump conditions (see also Lyu & Kan 1986)
to
arrive at jump conditions (see also Lyu & Kan 1986)