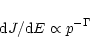1 Introduction

Diffusive shock acceleration (Axford et al. 1977; Krymsky 1977; Bell 1978; Blandford & Ostriker 1978) is a universal mechanism for the acceleration of non-thermal particle populations (Drury 1983; Blandford & Eichler 1987). Since energetic particles can be confined near the shock by plasma turbulence, they are accelerated due to two effects: (i) first-order Fermi acceleration due to multiple crossings of the shock compression front and (ii) stochastic second-order Fermi acceleration in the turbulent fields near the shock. Assuming that the turbulence consists of low-frequency waves on both sides of the shock enables one to investigate the relative importance of these two mechanisms. In this picture, the presence of the second-order Fermi effect requires waves propagating in both directions relative to the mean magnetic field. This condition is always satisfied in the shock's downstream region since an upstream Alfvén wave, when transmitted through a fast-mode shock, converts to two downstream waves propagating in both directions relative to the field (McKenzie & Westphal 1969). However, a consideration of the acceleration time scales of the two mechanisms shows that (i) is much faster than (ii), and should dominate acceleration under the assumption that the upstream waves are self-generated by the cosmic rays streaming against the plasma flow and, therefore, propagating in the backward direction relative to the flow (Vainio & Schlickeiser 1998, 1999).

When the second-order Fermi acceleration is neglected one obtains the canonical power-law (over momentum) test-particle energy spectrum,

$${\rm d}J/{\rm d}E\propto p^{-\Gamma }$$ (1)

at the shock. Here, $\Gamma =(r_{k}+2)/(r_{k}-1)$ and r_k=V_n,1/V_n,2 is the scattering-center compression ratio at the shock, V_n,1[2] is the normal component of the mean velocity of the upstream [downstream] scattering centers as measured in the frame of the shock. In general, the scattering center compression ratio is not the same as the gas compression ratio r=u_n,1/u_n,2 given by the ratio of normal plasma flow speeds, u_n,1[2]. In particular, scattering-center compression is not limited by the limiting value of $r<(\gamma _{\rm g}+1)/(\gamma _{\rm g}-1)$, where $\gamma _{\rm g}$is the polytropic index of the gas equaling 5/3 for an isotropic, adiabatic, non-relativistic gas.

Vainio & Schlickeiser (1998) studied the transmission of Alfvén waves through a parallel shock wave and calculated the resulting scattering-center compression ratio for a model neglecting the effect of waves on the shock's gas compression ratio. They showed that the scattering-center compression ratio tends to infinity at shocks with $r\to (\gamma _{\rm g}+1-\gamma _{\rm g}\beta )/(\gamma _{\rm g}-1)$, where $\beta \equiv 8\pi P_{1}/B_{0}^{2}$ is the upstream plasma beta, and P₁ and B₀ are the (isotropic) upstream gas pressure and the ordered magnetic field, respectively. At this limit, the Alfvénic Mach number of the shock, $M\equiv u_{1}/V_{\rm A1}\to r^{1/2}$, and the downstream backward Alfvén waves become standing waves in the shock frame yielding formally infinite intensities for these waves. This singularity is not a physical one, and is removed by the inclusion of wave pressure and energy flux to the shock's Rankine-Hugoniot equations (Vainio & Schlickeiser 1999). The scattering-center compression ratios remain high also in the self-consistent wave-transmission model which, therefore, is able to produce test-particle spectra that are harder than the limiting value of $\Gamma =2$occurring for r_k=r=4 in the original magnetostatic formulation of diffusive test-particle acceleration at non-relativistic shocks.

Anisotropic gas pressure modifies the dispersion relation of the low-frequency (Alfvén) waves. As noted by Schlickeiser & Vainio (1998), the important effects on particle acceleration in the model of Vainio & Schlickeiser (1998, 1999) were the result of the inclusion of finite phase speeds of the waves into the theory. Furthermore, pressure anisotropies also modify the jump relations at the shock in a non-trivial way. We know from observations that the pressure in the solar wind is anisotropic (see, e.g., Marsch 1991 for a review). Particle reflection from the shock also adds its contribution to the pressure anisotropy, so the gas pressure just upstream a shock is probably anisotropic even if the far upstream conditions were isotropic.

The purpose of this paper is to investigate the influence of pressure anisotropies on the wave transmission problem, shock compression ratios, and the resulting test-particle acceleration at parallel shocks. Although we will discuss briefly the pressure anisotropies associated with nonthermal particles, it is beyond the scope of the present study to develop a theory with self-consistent determination of pressure anisotropies around the shock. Thus, the effects of anisotropy are studied in a simplified way treating the anisotropy of the gas on both sides of the shock as a known parameter, and constraining its values so that the plasma stays stable against the upstream firehose stability criterion. Similar ideas have been employed previously by, e.g., Lyu & Kan (1986) in a study of plasma parameters at shocks measured in near-Earth space.