

Up: Probable asteroidal origin of
Subsections
As discussed in Sect. 2.1, in this paper we use the time given by Ben-Menahem
(see Table 4) with an uncertainty prudently estimated equal to 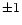 min.
In two minutes the Earth moves along its orbit approximately by
min.
In two minutes the Earth moves along its orbit approximately by
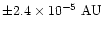 .
We therefore assumed the same uncertainty
for the components of the heliocentric vector of the position of the TCB at the
time of its collision with the Earth.
For our purposes the accuracy of the position is very high, and if we
knew the velocity vector with similar accuracy, the problem
of the origin of TCB would be simpler.
However, we have very poor estimation of the velocity, both its magnitude
and its direction.
.
We therefore assumed the same uncertainty
for the components of the heliocentric vector of the position of the TCB at the
time of its collision with the Earth.
For our purposes the accuracy of the position is very high, and if we
knew the velocity vector with similar accuracy, the problem
of the origin of TCB would be simpler.
However, we have very poor estimation of the velocity, both its magnitude
and its direction.
In the discussion that follows, we consider the Earth orbiting on
a circular orbit (with the radius
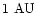 )
in the ecliptic plane. Also we assume, that the TCB moved on a
heliocentric elliptical orbit.
)
in the ecliptic plane. Also we assume, that the TCB moved on a
heliocentric elliptical orbit.
Knowing the exact moment in time at which the explosion
took place and that it happened very close to the Earth's surface enables
us to estimate the direction of the line of nodes of the orbit. From the theory of
the Earth's orbital motion we found the ecliptic longitudes of two points at
which this line crosses the ecliptic:
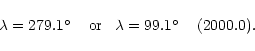 |
(6) |
To decide which of these longitudes corresponds to the ascending
node we need additional information. For this purpose
we used parameters of the geocentric trajectory from Table 4
illustrated in Fig. 3.
As we see, both radiant rectangles are plotted below the
line of the ecliptic, hence all the TCB geocentric velocity vectors,
as well as the corresponding heliocentric vectors which resulted,
point to the Northern ecliptic hemisphere. Therefore the TCB must have collided
with the Earth at the ascending node of the orbit,
and consequently the longitude of this node is equal to:
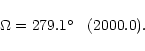 |
(7) |
The collision with the Earth occurred at the heliocentric distance
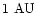 and at the ascending node of the orbit, so
we have the following crossing condition:
and at the ascending node of the orbit, so
we have the following crossing condition:
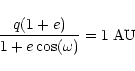 |
(8) |
where q is the perihelion distance, e the eccentricity, 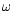 the argument of the perihelion of TCB orbit.
the argument of the perihelion of TCB orbit.
Condition (8) is not fulfilled for all trios
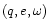 ,
in particular, the orbits for which
,
in particular, the orbits for which
| (q>1) |
|
|
(9) |
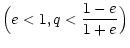 |
|
|
(10) |
are ruled out, in the sense that they are either too large or too
narrow to cross the Earth's orbit. The limiting cases are the orbits tangent to the
Earth's circle at the perihelion or the aphelion points (see Fig. 4).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H2886F4.ps}\end{figure}](/articles/aa/full/2001/39/aah2886/Timg146.gif) |
Figure 4:
The limiting cases for the TCB heliocentric orbits. All orbits with
perihelion distances q>1 or aphelion distances Q<1 cannot cross the
Earth's orbit (dashed circle). |
The fact that the collision took place at the ascending node and
was observed on the daytime side of the Earth limits
the argument of perihelion, i.e.:
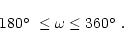 |
(11) |
Condition (10) can be used to find the smallest value of the
aphelion distance
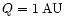 of the possible TCB orbits, and the
smallest semi-major axis
of the possible TCB orbits, and the
smallest semi-major axis
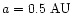 .
.
![\begin{figure}
\par {
\hbox{
\includegraphics[scale=0.7]{H2886F5a.ps}\includegraphics[scale=0.7]{H2886F5b.ps} }
}
\end{figure}](/articles/aa/full/2001/39/aah2886/Timg152.gif) |
Figure 5:
a) The left panel illustrates q-e distribution of 666 NEO
(Apollo open circles, Aten open squares, Amor x-es, comets +es),
for which the minimum distance between them and
the Earth's orbit is smaller than
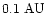 .
The sloping solid lines trace the limits for the orbits with .
The sloping solid lines trace the limits for the orbits with
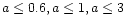 AU. The dashed lines correspond to the
orbits with (from bottom to top) AU. The dashed lines correspond to the
orbits with (from bottom to top)
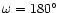 and
and
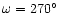 .
We only found nine objects (two comets and seven NEA)
with the perihelion distance .
We only found nine objects (two comets and seven NEA)
with the perihelion distance
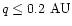 .
b) The right panel
shows the same distribution of elements of the TCB orbits calculated
for two sets of parameters .
b) The right panel
shows the same distribution of elements of the TCB orbits calculated
for two sets of parameters
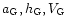 taken from
Table 4.
At the top, we have the points corresponding to the asteroidal solutions for
the TCB, while at the bottom, on the right, the cometary ones.
taken from
Table 4.
At the top, we have the points corresponding to the asteroidal solutions for
the TCB, while at the bottom, on the right, the cometary ones. |
However, as we see in Fig. 5, the perihelion distances are
smaller than
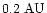 for a few of the small bodies observed.
If we agree that this is true in case of the TCB, then the following lower
limit for the semi-major axis is:
for a few of the small bodies observed.
If we agree that this is true in case of the TCB, then the following lower
limit for the semi-major axis is:
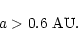 |
(12) |
The upper limit for q is given by condition (9), and there is no
explicit upper limit for the semi-major axis.
Using condition (12) and assuming that the TCB's orbit was elliptical
enable us to obtain the explicit lower and upper limits of the heliocentric
orbital speed of the TCB at the moment of the collision, in [kms-1]:
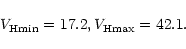 |
(13) |
In the right-hand panel of Fig. 5 we plotted the distribution of
the values of e and q corresponding to the geocentric intervals of the TCB
parameters given in Table 4.
We see that for a part of the cometary solutions the eccentricities of
the orbits are beyond the assumed upper limit.
In Table 5 we summarized the assumed and the deduced limits on the
heliocentric dynamic parameters of the TCB.


Up: Probable asteroidal origin of
Copyright ESO 2001
![]() )
in the ecliptic plane. Also we assume, that the TCB moved on a
heliocentric elliptical orbit.
)
in the ecliptic plane. Also we assume, that the TCB moved on a
heliocentric elliptical orbit.
![]() and at the ascending node of the orbit, so
we have the following crossing condition:
and at the ascending node of the orbit, so
we have the following crossing condition:
![]() the argument of the perihelion of TCB orbit.
the argument of the perihelion of TCB orbit.
![]() ,
in particular, the orbits for which
,
in particular, the orbits for which
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H2886F4.ps}\end{figure}](/articles/aa/full/2001/39/aah2886/Timg146.gif)
![\begin{figure}
\par {
\hbox{
\includegraphics[scale=0.7]{H2886F5a.ps}\includegraphics[scale=0.7]{H2886F5b.ps} }
}
\end{figure}](/articles/aa/full/2001/39/aah2886/Timg152.gif)
![]() for a few of the small bodies observed.
If we agree that this is true in case of the TCB, then the following lower
limit for the semi-major axis is:
for a few of the small bodies observed.
If we agree that this is true in case of the TCB, then the following lower
limit for the semi-major axis is: