

Up: Probable asteroidal origin of
Subsections
We assume that the Tunguska explosion was caused by a single solid body, which
collided with the Earth, and that this body moved around the Sun on a closed
orbit. We can therefore describe its cosmic trajectory as in the case of meteoroids,
namely, by means of the moment of time, the geocentric speed and the radiant geocentric
coordinates. The values of these parameters should correspond to the point at which the TCB
entered the Earth's atmosphere. Therefore within a short interval of time the TCB trajectory
can be modelled by a straight-line section whose orientation relative to the local
horizontal reference frame is given by the azimuth and the
height of its radiant point![[*]](/icons/foot_motif.gif) .
.
We started (Sect. 2.1) with an extremely detailed analysis of the literature available on the
Tunguska event, from which we obtained the data summarized in Table 1. With the help of
theoretical models we then reduced the parameter ranges (Sects. 2.2 and 2.3) to those
listed in Table 4. This choice of parameters made it possible to make most limited
calculations whilst preserving the more plausible solutions.
In order to obtain the parameters necessary for the calculations recorded in this paper,
we consider objective data and testimonies of the Tunguska event. Two kinds of objective
data on the Tunguska explosion are available: seismic and barometric registrations,
recorded immediately after the event, and data on forest devastation, systematically
collected 50-70 years later.
Seismic records from Irkutsk, Tashkent, and Tiflis were published together, two
years after the event (Levitskij 1910); those from Jena - three years later (Catalogue 1913).
However, it was only in 1925, that the origin of these seismic waves was connected to the
Tunguska event and a first determination of the explosion time as
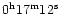 UT was obtained (Voznesenskij 1925).
UT was obtained (Voznesenskij 1925).
Barograms were recorded in a great number of observatories throughout the world.
From the barograms of 13 Siberian stations, the explosion time was found equal
to
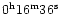 UT (Astapovich 1933).
UT (Astapovich 1933).
These two kinds of data were subsequently analysed more precisely taking into
account the exact distances and the properties of seismic and atmospheric waves.
A first result (
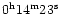 UT), based on the
seismic data of Jena and Irkutsk
only, was obtained by Pasechnik (1971). Two more complete analyses, using the
whole set of seismic and barographic data, were independently performed
by Ben-Menahem (1975) and Pasechnik (1976). They found practically the same
value for the time the seismic waves started (see Table 1). Pasechnik (1976)
calculated that the time of the explosion in the atmosphere was 7-30 s
earlier depending on the height and energy of the explosion.
This interval was subsequently reduced to 2-20 s (Pasechnik 1986),
which was much lower than the experimental uncertainty quoted in 1976 (
UT), based on the
seismic data of Jena and Irkutsk
only, was obtained by Pasechnik (1971). Two more complete analyses, using the
whole set of seismic and barographic data, were independently performed
by Ben-Menahem (1975) and Pasechnik (1976). They found practically the same
value for the time the seismic waves started (see Table 1). Pasechnik (1976)
calculated that the time of the explosion in the atmosphere was 7-30 s
earlier depending on the height and energy of the explosion.
This interval was subsequently reduced to 2-20 s (Pasechnik 1986),
which was much lower than the experimental uncertainty quoted in 1976 (
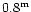 ).
In the 1986 paper, however, Pasechnik revised his previous results obtaining a
value equal to
).
In the 1986 paper, however, Pasechnik revised his previous results obtaining a
value equal to
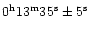 UT.
UT.
Taking into account the values given in Table 1 and the uncertainties here
discussed, in our calculations (Table 4) we use the time given by
Ben-Menahem with an uncertainty prudently estimated
equal to 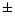 1 min. We consider this value as the instant at which the
bolide entered the Earth's atmosphere. That instant precedes both the time of the
atmospheric explosion and the time the seismic waves started. However, the
differences are negligible when compared with uncertainties affecting other data.
1 min. We consider this value as the instant at which the
bolide entered the Earth's atmosphere. That instant precedes both the time of the
atmospheric explosion and the time the seismic waves started. However, the
differences are negligible when compared with uncertainties affecting other data.
![\begin{figure}
\par\includegraphics[scale=0.3,angle=270]{H2886F1.eps}\end{figure}](/articles/aa/full/2001/39/aah2886/Timg69.gif) |
Figure 1:
Kulik's 1928 photo of fallen Tunguska trees. |
The data on forest devastation is a second kind of objective data on the event.
This data includes the directions of flattened trees, which can help us to obtain
information on the coordinates of the wave propagation centres and on the final
trajectory of the TCB. Although the radial orientation of the fallen trees was discovered
by Kulik since 1927 (see Fig. 1),
systematic measurements of the azimuth of fallen trees were begun during the two
great post-war expeditions organised by the Academy of Sciences in 1958 and 1961
(Florenskij 1960, 1963) and during the Tomsk 1960 expedition. Under
the direction of Fast, with the help of Boyarkina, this work was continued for
two decades during ten different expeditions from 1961 up to 1979. A total of 122 people, mainly from Tomsk University, participated in these measurements. The data
collected is published in a catalogue in two parts: the first one (Fast et al. 1967)
contains the data obtained by six expeditions (1958-1965), which include the measurement
of the direction of more than 60 thousands fallen trees on 859 trial areas equal to 2500 or 5000 m2 and chosen throughout the whole devastated forest. In the
second part (Fast et al. 1983) the data of the areas N
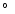 860-1475, collected by
the six subsequent expeditions (1968-1976) were given.
860-1475, collected by
the six subsequent expeditions (1968-1976) were given.
From the data collected during the first three expeditions, Fast (1963) obtained
the epicentre coordinates
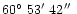 N and
N and
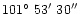 E. These values are very close to the final ones
E. These values are very close to the final ones
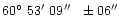 N,
N,
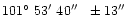 E, calculated by Fast (1967)
analysing the whole set of data from the first part of the catalogue (Fast et al. 1967).
Zolotov (1969) contemporarily performed an independent mathematical analysis of the same
data and obtained the second values quoted in Table 1. The coordinates of
Fast's epicentre
E, calculated by Fast (1967)
analysing the whole set of data from the first part of the catalogue (Fast et al. 1967).
Zolotov (1969) contemporarily performed an independent mathematical analysis of the same
data and obtained the second values quoted in Table 1. The coordinates of
Fast's epicentre![[*]](/icons/foot_motif.gif) with the uncertainties quoted,
corresponding to about 200 m on the ground, were subsequently confirmed
in all Fast's papers and are here used in our calculations (Table 4).
with the uncertainties quoted,
corresponding to about 200 m on the ground, were subsequently confirmed
in all Fast's papers and are here used in our calculations (Table 4).
Many witnesses have heard a single explosion. Some of them have heard
multiple explosions, that can be echoes.
Examining the directions of fallen trees seen on the aero-photographic survey performed
in 1938, Kulik suggested (1939, 1940) the presence of 2-4 secondary centres of wave
propagation. This hypothesis was not confirmed, though not definitely ruled out, by Fast's
analyses and by seismic data investigation (Pasechnik 1971, 1976, 1986). Some hints on its
likelihood were given e.g. by Serra et al. (1994) and Goldine (1998). However, in absence of a
sure conclusion on the matter, in this paper we prefer to assume, as one usually does, that
a single explosion caused the Tunguska event. If there were many bodies, like in the case of
the Shoemaker-Levy 9 comet, all orbits would be very similar and the
differences between the individual orbits would be much smaller than the
differences due to the uncertainties in the parameters chosen.
Data on forest devastation include, not only fallen tree directions, but also the
distances that different kind of trees were thrown, the pressure necessary to do this,
information on forest fires and charred trees, data on traumas observed in the wood of
surviving trees, and so on (see, e.g., Florenskij 1963; Vorobjev et al. 1967;
Longo & Serra 1995; Longo 1996). From this data, other parameters of the trajectory
can be obtained. First of all, the height of the explosion and the trajectory azimuth.
The height of the explosion is closely related to the value of the energy emitted,
usually estimated equal to about 10-15 Mton (Hunt 1960; Ben-Menahem 1975),
although some authors considered the energy value to be higher, up to 30-50 Mton
(Pasechnik 1971, 1976, 1986). In correspondence with the first energy range,
which seems to have better grounds, the height of the explosion was found equal
to 6-14 km. A height of
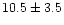 km was obtained by Fast (1963) from data
on forest devastation. Using more complete data on forest devastation,
Bronshten & Boyarkina (1971) subsequently obtained a height equal to
km was obtained by Fast (1963) from data
on forest devastation. Using more complete data on forest devastation,
Bronshten & Boyarkina (1971) subsequently obtained a height equal to
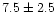 km. From seismic data, Ben-Menahem deduced an explosion
height of 8.5 km. Data on the forest devastation examined, taking into
account the wind velocity gradient during the TCB's flight (Korotkov & Kozin 2000),
gave an explosion height in the range 6-10 km. To calculate the
TCB's geocentric speed we used a height equal to 8.5 km (see Sect. 2.2),
which agrees, taking into account the uncertainties quoted, with the data
summarized herein and listed in Table 1.
km. From seismic data, Ben-Menahem deduced an explosion
height of 8.5 km. Data on the forest devastation examined, taking into
account the wind velocity gradient during the TCB's flight (Korotkov & Kozin 2000),
gave an explosion height in the range 6-10 km. To calculate the
TCB's geocentric speed we used a height equal to 8.5 km (see Sect. 2.2),
which agrees, taking into account the uncertainties quoted, with the data
summarized herein and listed in Table 1.
Two other parameters are needed to compute the possible TCB orbits: the final
trajectory azimuth (a) and its inclination (h) over the horizon.
A close inspection of seismograms of Irkutsk station, made by Ben-Menahem (1975),
showed that the ratio between East-West and North-South components is
about 8:1, even though the response of the two seismometers is the same. Since the
Irkutsk station is South of epicentre, Ben-Menahem (1975) inferred that this
was due to the ballistic wave and therefore the azimuth should be between
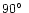 and
and
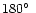 ,
mostly eastward. However, it is not possible to
obtain more stringent constraints on the azimuth from seismic data.
,
mostly eastward. However, it is not possible to
obtain more stringent constraints on the azimuth from seismic data.
Analysing the data on flattened tree directions from the first part of his catalogue,
Fast found a trajectory azimuth
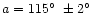 as the
symmetry axis of the "butterfly'' shaped region (Fast 1967). An independent mathematical
analysis of the same data gave
as the
symmetry axis of the "butterfly'' shaped region (Fast 1967). An independent mathematical
analysis of the same data gave
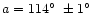 (Zolotov 1969). Having made
another set of measurements, Fast subsequently suggested a value of
(Zolotov 1969). Having made
another set of measurements, Fast subsequently suggested a value of
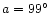 (Fast et al. 1976). In this second work, the differences between the mean measured
azimuths of fallen trees and a strictly radial orientation were taken into account.
No error was given for this new value, but a close examination of Fast's writings suggests
that an uncertainty of
(Fast et al. 1976). In this second work, the differences between the mean measured
azimuths of fallen trees and a strictly radial orientation were taken into account.
No error was given for this new value, but a close examination of Fast's writings suggests
that an uncertainty of
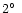 was considered. The Koval's group subsequently collected
complementary data on forest devastation and critically re-examined Fast's work.
They obtained a trajectory azimuth
was considered. The Koval's group subsequently collected
complementary data on forest devastation and critically re-examined Fast's work.
They obtained a trajectory azimuth
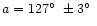 and an inclination
angle
and an inclination
angle
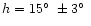 (Koval' 2000).
(Koval' 2000).
The witness accounts can be analysed to obtain information on the trajectory
azimuth. A great part of the testimonies were collected more than 50 years after the
event. They are often contradictory or unreliable. However a thorough examination of
this material can give reasonable results. We here report some important results of such
analyses (see Fig. 2, re-elaborated from Bronshten 2000c).
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{H2886F2.eps}\end{figure}](/articles/aa/full/2001/39/aah2886/Timg85.gif) |
Figure 2:
Map with the location of the more reliable witnesses of the Tunguska event:
1 - visual observations, 2 - acustical records and barograms,
3 - azimuths spanning from
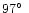 to
to
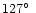 ,
used in the present calculations. ,
used in the present calculations. |
From a critical analysis of all the eyewitness testimonies collected in the
catalogue of Vasilyev et al. (1981), Andreev (1990) deduced
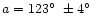 and an inclination angle
and an inclination angle
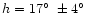 .
Zotkin & Chigorin (1991) using
the data in the same catalogue obtained:
.
Zotkin & Chigorin (1991) using
the data in the same catalogue obtained:
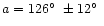 and
and
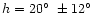 ,
while, from partial data, Zigel' (1983) deduced
,
while, from partial data, Zigel' (1983) deduced
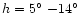 .
A
different analysis of the eyewitness data (Bronshten 2000c), gave
.
A
different analysis of the eyewitness data (Bronshten 2000c), gave
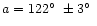 and
and
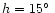 .
In the same book a mean value
.
In the same book a mean value
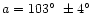 ,
obtained
from forest devastation data, is given.
,
obtained
from forest devastation data, is given.
Sekanina (1983, 1998) studied the Tunguska event on the basis of
superbolide theories and analysed the data available and eyewitness
testimonies. He suggested a geocentric speed of 14 kms-1 (see the discussion in
Sect. 2.2), an inclination over the horizon
 ,
and an azimuth
,
and an azimuth
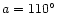 .
.
All these values for a and h are listed in Table 1 and were used to choose
the starting parameters of our calculations listed in Table 4. When the experimental
error is not explicitly given, we used 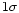 .
.
One of the most important parameters that can be inferred from atmospheric
studies is the geocentric speed. Even though the fragmentation of a small asteroid
or comet depends on several parameters, the speed appears to be the key in the
understanding of the impact physics. Once the speed is known, it allows
us to calculate the mass (from the energy released in the explosion), and to have a first,
but not conclusive idea about the nature of the TCB. Indeed,
dynamic studies of minor bodies in the Solar System have long suggested
that it is very unlikely to find an asteroid with a geocentric speed higher than about
30-32 kms-1. Generally speaking, it is common among researchers on impact physics,
to consider indicative values of speed associated to specific bodies. For example,
Chyba et al. (1993) used 15 kms-1 for iron/stone/carbonaceous bodies (asteroids),
25 kms-1 for short period comets, and 50 kms-1 for long period comets.
Hills & Goda (1993) considered a set of values inferior to 30 kms-1for asteroids, and up to 70 kms-1 for comets. So, a TCB speed of,
for example, 50 kms-1 would strengthen the hypothesis of cometary
nature of the TCB.
Speed is strictly related to the break-up height of the cosmic body. In the TCB's
case, the height is known from studies on the devastated area and seismic records
(see Table 1). It is therefore possible to calculate the speed, but we need a model for
fragmentation. Present models consider that fragmentation begins when the following
condition is fulfilled:
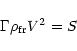 |
(1) |
where
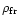 is the density of the atmosphere at the
fragmentation height, V is the speed of the body, S is the material mechanical
strength, and
is the density of the atmosphere at the
fragmentation height, V is the speed of the body, S is the material mechanical
strength, and 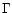 is the drag coefficient, commonly set equal to 1 (sphere).
The term
is the drag coefficient, commonly set equal to 1 (sphere).
The term
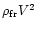 refers to the dynamic pressure on the front
of the cosmic body. Adopting these criteria, Sekanina (1983) suggested
a geocentric speed of 14 kms-1.
refers to the dynamic pressure on the front
of the cosmic body. Adopting these criteria, Sekanina (1983) suggested
a geocentric speed of 14 kms-1.
However, observations of very bright bolides prove that large meteoroids or
small asteroids disintegrate at dynamic pressures lower than their mechanical
strength (e.g. Ceplecha 1996; see also Foschini 2001 for a
recent review). Therefore, Foschini (1999, 2001) developed
a new model studying the hypersonic flow around a small asteroid entering the
Earth's atmosphere. This model is compatible with fragmentation data from
superbolides. According to Foschini's model, the condition for
fragmentation depends on two regimes: steady state, when the Mach number does not
change, and unsteady state, when the Mach number has strong changes. In the latter
case, the distortion of shock waves interacts with turbulence, producing a
local amplification of dynamic pressure (Foschini 2001). In the first case,
when the Mach number is constant, the compression due to shock waves tends to
suppress the turbulence and therefore the viscous heat transfer is
negligible and we can consider the flux as adiabatic (Foschini 1999).
The Tunguska Cosmic Body was under these conditions in the last part of its
trajectory in the atmosphere, therefore it is possible to calculate the maximum
possible speed at the point of fragmentation (Foschini 1999):
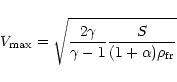 |
(2) |
where 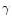 is the specific heat ratio,
is the specific heat ratio, 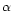 is the coefficient
of ionisation. Foschini (1999), using h=8.5 km,
is the coefficient
of ionisation. Foschini (1999), using h=8.5 km, 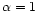 (full ionisation),
and
(full ionisation),
and
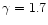 ,
found that the only reasonable solution is with S=50 MPa
(typical of a stony asteroid), which leads to a speed of 16 kms-1 and an inclination
of
,
found that the only reasonable solution is with S=50 MPa
(typical of a stony asteroid), which leads to a speed of 16 kms-1 and an inclination
of
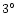 .
.
However, Bronshten (2000a) raised a doubt about the validity of the value of the
specific heat ratio 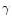 ,
which, according to him, should be equal
to 1.15, calculated from using the equation:
,
which, according to him, should be equal
to 1.15, calculated from using the equation:
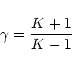 |
(3) |
where K is the density ratio across the shock, which in turn is
given by the equation (see Zel'dovich & Raizer 1966):
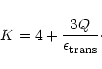 |
(4) |
In the Eq. (4), the sum of Q and
 gives the internal
energy of the gas, i.e. the sum of translational energy
gives the internal
energy of the gas, i.e. the sum of translational energy
 and Q,
the potential energy and the energy of the internal degree of freedom of the particles
(vibrational and rotational, for molecules). According to Eqs. (3)
and (4),
and Q,
the potential energy and the energy of the internal degree of freedom of the particles
(vibrational and rotational, for molecules). According to Eqs. (3)
and (4), 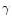 for air molecules under shock compression reaches
the value of 1.15 (Bronshten 2000a).
for air molecules under shock compression reaches
the value of 1.15 (Bronshten 2000a).
Foschini (1999) used a value of
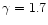 ,
according to the
experimental investigation of hypervelocity impact by Kadono & Fujiwara (1996).
Their original experimental results gave a value
of
,
according to the
experimental investigation of hypervelocity impact by Kadono & Fujiwara (1996).
Their original experimental results gave a value
of
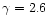 ,
that the authors considered too high. They modified the
calculations considering that the expansion velocity of the leading edge of
the plasma was about twice that of the isothermal sound
speed, obtaining a more reasonable
,
that the authors considered too high. They modified the
calculations considering that the expansion velocity of the leading edge of
the plasma was about twice that of the isothermal sound
speed, obtaining a more reasonable
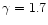 .
.
However, none of the above mentioned authors considered that the gas envelope
around any cosmic body entering the Earth's atmosphere is in the state of plasma,
in which there are electric and magnetic fields
(see e.g., Beech & Foschini 1999) limiting the degree of freedom of particles.
According to the law of equipartition of energy, the specific heat ratio can be
written (Landau & Lifshitz 1980):
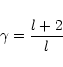 |
(5) |
where l is the degree of freedom of particles. For example, l=3
for a monatomic gas or metal vapours, because the atom has three degrees of freedom
(translation of atoms along x, y, z directions) and
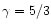 .
For plasma,
the presence of electric fields forces the ions or even ionised molecules, if present,
to move along the field lines, and therefore l=1. This implies that
.
For plasma,
the presence of electric fields forces the ions or even ionised molecules, if present,
to move along the field lines, and therefore l=1. This implies that
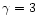 ,
close to Kadono & Fujiwara's original experimental value of 2.6
(Kadono & Fujiwara 1996).
,
close to Kadono & Fujiwara's original experimental value of 2.6
(Kadono & Fujiwara 1996).
We calculated a set of possible speeds, depending on the mechanical strength, for
different values of specific heat ratio and ionisation coefficient
(Table 2). Concerning the air density at the fragmentation height,
we have to consider that the height of the airburst is not
the point of first fragmentation. Generally, studies on superbolides show
that the break-up begins about one scale height before the airburst. So, we
consider that the TCB began to break up at about 15 km, to which corresponds
a value of
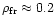 kg/m3 (Allen 1976).
kg/m3 (Allen 1976).
As already noted by Ceplecha (1999, personal communication; cf. Foschini
2000), the key point in fragmentation is how the ablation changes the hypersonic
flow. If the ablation does not appreciably modify the shocked air around the TCB,
the carbonaceous body hypothesis could be plausible. However, if the shocked
air is mixed with ionised atoms from the TCB so that the gas around the body is
fully ionised or even plasma, the only possible solution appears to be an asteroidal body
(stony or even iron). The values obtained in Table 2 show that, in any case,
it is very unlikely that a cometary body could reach such a low height, because
it would have an unphysical low value of speed.
It should be noted that these results are only indicative: for S we have
considered the commonly used values of 1, 10, 50, and 200 MPa. On the other hand,
if we start to search for the mechanical strength from the speed value, we obtain
comparable results, with some interesting aspects. We know that Sekanina (1983)
suggested V=14 kms-1 and Foschini (1999) found V=16 kms-1. With the new
fragmentation theory, we can calculate the mechanical
strength that the TCB would have to break-up at the given height.
Table 3 shows some results obtained in the same conditions for
air flow as in Table 2. It appears clear that the asteroidal nature of the
TCB is still the most probable, even though cases (C) and (D) - the Bronshten's
values - have the strength of a carbonaceous body. The cometary strength is very
close and, given the large uncertainties, it is not possible to exclude it at all.
In Table 4 we gathered all trajectory data used in this
paper. The moment of time is determined with sufficient accuracy to study the
hypothesis of the TCB's origin. We chose the value given by Ben-Menahem (1975)
as the instant at which the bolide entered the
Earth's atmosphere. The remaining parameters are not known precisely enough and
we needed to reduce the possible ranges. Therefore, we started from data
obtained directly from measurements or easy
calculations (see Sect. 2.1) and from those obtained by modelling (see
Sect. 2.2). We added one
more theory: Kresák (1978) suggested that the TCB might be a
fragment of the comet Encke.
He used the apparent radiant calculated by Zotkin (1966), concluding that it was
very close to the radiant of 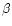 -Taurids. In addition, this meteor shower
has its maximum activity at the end of June. Both the TCB and the meteor shower had
the same solar longitude of the closest approach point of the comet to the Earth.
For the TCB, Kresák proposed an apparent radiant with
-Taurids. In addition, this meteor shower
has its maximum activity at the end of June. Both the TCB and the meteor shower had
the same solar longitude of the closest approach point of the comet to the Earth.
For the TCB, Kresák proposed an apparent radiant with
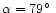 and
and
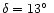 .
As a fragment of the comet Encke, the geocentric speed
can be inferred as
.
As a fragment of the comet Encke, the geocentric speed
can be inferred as 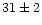 kms-1.
kms-1.
From all this data we selected two main possibilities, commonly referred to in
literature as typically asteroidal and typically cometary. We keep the azimuth
spanning over a wide range of values, from
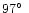 to
to
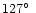 (see Fig. 2),
while we reduced the possible values of the inclination over the
horizon to two ranges
(see Fig. 2),
while we reduced the possible values of the inclination over the
horizon to two ranges
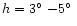 and
and
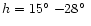 .
Two
velocity ranges were considered
V = 14-16 kms-1 and
V = 30-32 kms-1.
.
Two
velocity ranges were considered
V = 14-16 kms-1 and
V = 30-32 kms-1.
The results are shown in Table 4. The first set (I), with low inclination
and low speed is commonly referred to as the "asteroidal'' hypothesis, while the
second set (II), with high inclination and high speed, is the "cometary'' one.
It is necessary to note the discrepancy with results on atmospheric dynamics
obtained in the previous section, which are consistent with a general asteroidal
hypothesis, but seem to admit a small possibility for comets with low speed. Surely,
one of the problems of studies on the TCB was the difficulty in
obtaining an atmospheric behaviour consistent with the interplanetary dynamics and
this problem was already encountered in combined studies (interplanetary and atmospheric
dynamics) of superbolides. As already underlined in a previous paper, according to
interplanetary dynamics there is a predominance of asteroidal bodies in the 1-10 m
size range, while ablation and fragmentation characteristics suggest that very weak bodies
are the most common type (Foschini et al. 2000). In this study, as we shall see,
the use of a new model for atmospheric dynamics allows us to overcome this
discrepancy (at least in principle, because of high uncertainties).
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{H2886F3.eps}\end{figure}](/articles/aa/full/2001/39/aah2886/Timg134.gif) |
Figure 3:
Two rectangles contain possible geocentric radiants of the TCB
trajectory in the spherical alt-azimuth reference frame. The origin of the frame
is fixed at the epicentre point of the explosion. The dotted curve is the ecliptic
on the celestial sphere; on the left the position of the Sun is marked, on the
right the position of the apex of the Earth orbital motion and the vernal
equinox are marked. All positions are calculated at the moment of the Tunguska
explosion. The top rectangle includes two "cometary'' TCB solutions
given by Zotkin (1966) and Kresak (1978), and Bronshten (1999). Inside the bottom
rectangle the "asteroidal'' solutions from Sekanina (1983) and Foschini (1999) are
plotted. Before plotting all radiants were corrected due to the zenithal
attraction and the diurnal motion of the Earth. |
In Fig. 3 in the alt-azimuth reference frame the rectangles of
the radiant points from Table 4 are plotted.
To fulfil the rules of meteor astronomy, the apparent pre-atmospheric
radiant coordinates
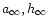 and the speed
and the speed
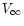 should be
corrected before any orbital calculation. Therefore, we corrected these
values accounting for the Earth rotation and gravity attraction (Ceplecha 1987);
we neglected the deceleration in atmosphere, because the mass loss by ablation
is minute when compared to the total estimated mass of the TCB
(
should be
corrected before any orbital calculation. Therefore, we corrected these
values accounting for the Earth rotation and gravity attraction (Ceplecha 1987);
we neglected the deceleration in atmosphere, because the mass loss by ablation
is minute when compared to the total estimated mass of the TCB
(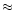 108-109 kg). The resulting corrected intervals of the geocentric
radiant and the speed
108-109 kg). The resulting corrected intervals of the geocentric
radiant and the speed
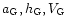 are placed in the
second column of Table 4. As one can see, for the "cometary'' parameters of
the TCB, the corrections are small. But this is not the case for the "asteroidal'' solutions of the
TCB's origin.
are placed in the
second column of Table 4. As one can see, for the "cometary'' parameters of
the TCB, the corrections are small. But this is not the case for the "asteroidal'' solutions of the
TCB's origin.


Up: Probable asteroidal origin of
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[scale=0.3,angle=270]{H2886F1.eps}\end{figure}](/articles/aa/full/2001/39/aah2886/Timg69.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{H2886F2.eps}\end{figure}](/articles/aa/full/2001/39/aah2886/Timg85.gif)
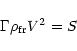
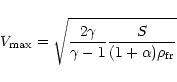
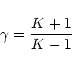
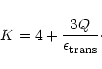
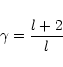
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{H2886F3.eps}\end{figure}](/articles/aa/full/2001/39/aah2886/Timg134.gif)