7 The derivative of the orbital period and the mass loss rate

In Sect. 4 it was found that the orbital ephemeris has a significant negative quadratic term, indicating a decreasing period. The derivative of the period is given by $\dot{P} \equiv {\rm d}P/{\rm d}t = 2b/P$, where b is the coefficient of E²of the quadratic ephemeris. Thus, $\dot{P} = -(1.30 \pm 0.04)\times 10^{-10}$if P=P₁ and $\dot{P} = -(2.60 \pm 0.09)\times 10^{-10}$if P=P₂ [note that $b(P_2) = 4\times b(P_1)$]. The relative period decrease is then $\dot{P}/P = - (1.15 \pm 0.04) \times 10^{-9}\, {\rm d}^{-1}$.

The period derivative is three orders of magnitudes larger than predicted by GB83 who assumed gravitational radiation to be the sole agent for angular momentum (AM) loss. Qualitatively, this difference is readily explained if the mass loss which gave origin to the formation of the planetary nebula is still ongoing.

In order to quantify this idea we assume that one or both binary components lose mass via a stellar wind. The ejected mass takes away rotational AM of the stars. In a close binary system such as MT Ser bound rotation may be assumed. Thus, rotational AM loss will result in a decrease of the binary orbit. In order to derive constraints on the mass loss from the system, me may therefore, in a reasonable approximation, equate the orbital angular momentum loss as indicated by the negative period derivative to the rotational AM loss of the component stars due to a stellar wind. This is an approximate approach because regarding the AM balance both, orbital and rotational contributions have to be considered, whereas equating the above mentioned quantities only the orbital angular momentum is regarded. While the orbital motion is certainly responsible for the major part of the total AM of the system, in view of the relative sizes of the components as derived in Sect. 5, and depending on their internal structure, the rotational angular momentum may not be negligible altogether. However, for an approximate determination of the mass loss from the system it will suffice to regard only the orbital AM loss here.

In a strongly idealized scenario we assume an isotropic wind to emanate from the stellar surface and to take away an amount of angular momentum corresponding to the AM of the wind mass due to the stellar rotation at the location where it left the star. The quantification of this concept for the individual stellar surface elements and the integration over the entire surface yields a rate of angular momentum loss of

$$\dot{J}_{\rm rot} = \frac{\pi}{3}\, \frac{\dot{M}}{P} \, R_{\rm eff}^2$$

where $\dot{M}$ is the entire mass loss rate from the star, $R_{\rm eff}$ is the effective stellar radius (assuming a spherical star) which - for the time being, but see below - is taken to be the geometrical radius, and P is the rotational period which is considered here as identical to the orbital period.

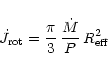
In an inertial reference frame the orbital AM, $J_{\rm orb}$, (assuming a circular orbit) can be expressed as a function of the period, P, the masses, M₁ and M₂, of the components (assumed to be point-like) and the orbital radius, a₁, of the primary star. The temporal derivative of the orbital AM, $\dot{J}_{\rm orb}$, is then the sum of the partial derivatives with respect to P, M₁, M₂and a₁. Of course, in a Keplerian orbit these are not independent. Since the derivative of the orbital period, $\dot{P}$, is a measured quantity, and because we are interested in the mass loss rates (i.e. $\dot{M}_1$ and $\dot{M}_2$) we use Kepler's third law to express a₁in terms of P, M₁ and M₂. This yields $\dot{a}_1$ in terms of $\dot{P}$, $\dot{M}_1$ and $\dot{M}_2$. Using the corresponding expression to eleminate $\dot{a}_1$ from the equation for $\dot{J}_{\rm orb}$, we finally get a (somewhat lengthy) expression for the derivative of the orbital angular momentum which depends on P, M₁, M₂, a₁, $\dot{P}$, $\dot{M}_1$ and $\dot{M}_2$. Except for the latter two quantities all are known either from direct observations or were derived within a specific model (see Table 6). Thus, choosing values for $\dot{M}_2$and $\dot{M}_2$ such that $\dot{J}_{{\rm rot},1} + \dot{J}_{{\rm rot},2} = \dot{J}_{\rm orb}$ gives us an estimate (within the numerous approximations involved) for the mass loss of the system.

For Model 1 we assume that only the primary (evolved) star loses mass. Then, $\dot{M}_{\rm tot} \equiv \dot{M}_1 + \dot{M}_2 = \dot{M}_1$. For Model 2 we investigate the cases $\dot{M}_{\rm tot} = \dot{M}_1$, $\dot{M}_{\rm tot} = \dot{M}_2$ and $\dot{M}_1 = \dot{M}_2 = 0.5 \, \dot{M}_{\rm tot}$. Within Model 1 agreement between $\dot{J}_{\rm rot}$ and $\dot{J}_{\rm orb}$is achieved for mass loss rates of $1.8\times 10^{-7}~M_\odot~{\rm yr}^{-1}$, $7.3\times 10^{-8}~M_\odot~{\rm yr}^{-1}$ and $2.4\times 10^{-8}~M_\odot~{\rm yr}^{-1}$ in the H, I and L cases, respectively.

In contrast, no solution exists for Model 2. For all mass loss rates the rotational angular momentum loss is less than the predicted orbital angular momentum loss. This is only different, if an "efficiency factor'' f for the rotational AM loss is introduced, assuming that $R_{\rm eff} = fR$, where R is the true geometrical radius of the star. This may be thought of as roughly simulating a magnetically coupled wind which dynamically decouples from the stellar rotation only at the radius $R_{\rm eff}$. It is then found that solutions for $\dot{M}$ such that $\dot{J}_{\rm rot} = \dot{J}_{\rm orb}$ exist for efficiency factors for Model 2.2.1, and - in the case of Model 2.2.2 - for ( $\dot{M}_{\rm tot} = \dot{M}_1$), ( $\dot{M}_1 = \dot{M}_2$) and ( $\dot{M}_{\rm tot} = \dot{M}_2$). The functional dependence between the efficiency factor and the total mass loss rate is shown in Fig. 4 for Model 1.1 (upper frame), Model 2.2.1 (case $\dot{M}_1 = \dot{M}_2$; middle frame) and Model 2.2.2 (case $\dot{M}_1 = \dot{M}_2$; lower frame).

Figure 4: Total mass loss rate from the stellar components of MT Ser necessary to explain the observed period derivative as a function of the efficiency factor for removal of rotational angular momentum by a stellar wind for Models 1.1 (assuming $\dot{M}_{\rm tot} = \dot{M}_1$) ( top), Model 2.2.1 ( $\dot{M}_1 = \dot{M}_2$) ( middle) and Model 2.2.2 ( $\dot{M}_1 = \dot{M}_2$) ( bottom). For details, see text.