

Up: An analysis of the MT Serpentis
4 Orbital ephemeris and light curve
According to an estimate of GB83 the time-scale for the decrease
of the orbital period of MT Ser due to gravitational radiation
is comparatively short. Therefore,
they urge other observers to obtain timings. The present light curves permit
us to measure the epochs of six minima (a further minimum occurred a few
minutes before the end of the observations, making an accurate timing
difficult; therefore it is not considered here).
The individual light curves were fitted by a spline which was then
evaluated to find the minima. The corresponding timings are listed
in Table 2 which also includes the minimum epochs
measured by GB83.
Table 2:
Times of minimum for MT Ser.
| HJD |
E |
O-C
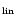 |
O-C
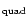 |
| 2444703.9734 |
-3347 |
-0.003785 |
-0.002478 |
| 2444705.9029 |
-3330 |
+0.000868 |
+0.002168 |
| 2445082.9480 |
0 |
+0.001618 |
+0.001618 |
| 2445084.8715 |
17 |
+0.000267 |
+0.000261 |
| 2445087.9277 |
44 |
-0.000651 |
-0.000667 |
| 2445115.6691 |
289 |
+0.000250 |
+0.000145 |
| 2445115.7829 |
290 |
+0.000823 |
+0.000718 |
| 2445117.7061 |
307 |
-0.000825 |
-0.000937 |
| 2445117.8197 |
308 |
-0.000450 |
-0.000562 |
| 2445118.7249 |
316 |
-0.001065 |
-0.001180 |
| 2450683.4683 |
49463 |
-0.002120 |
-0.002217 |
| 2450686.4165 |
49489 |
+0.002232 |
+0.002145 |
| 2450686.5278 |
49490 |
+0.000334 |
+0.000247 |
| 2450687.4341 |
49498 |
+0.000772 |
+0.000688 |
| 2450687.5454 |
49499 |
-0.001127 |
-0.001210 |
| 2450688.4521 |
49507 |
-0.000201 |
-0.000281 |
The ephemeris determined by GB83 are accurate enough so that no
cycle count ambiguities occur at the epoch of our measurements. The cycle
numbers of the minima observed here are also quoted in Table
2. Combining the present minimum timings with those
of GB83, the much longer time base permits us to determine a considerably
more accurate period for MT Ser. Improved values for the minimum epoch, T0,
and the period, P, were determined by minimizing 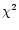 of the O-C
values of the minimum times. The revised ephemeris is:
of the O-C
values of the minimum times. The revised ephemeris is:
| HJD (min) |
= |
2445082.9461 |
+ |
0.113226533 |
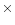 |
E |
|
|
| |
|
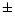 4
4 |
|
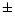 15
15 |
|
|
|
|
The O-C values of the individual minima with respect to this ephemeris
are also given in Table 2.
Although according the to model of GB83 a change of the period due
to gravitational radiation should only become detectable on time scales of
100 years or more, we also fitted a quadratic ephemeris to the minimum timings:
| HJD(min)= |
2445082.94638 |
+ |
0.11326899 |
E- |
7.36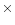 10-12 10-12 |
E2 |
|
|
|
| |
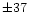 |
|
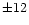 |
|
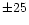 |
|
|
|
|
Table 2 contains the O-C values also for this case. As
can be seen, the quadratic term is highly significant within the formal
error. The issue of the period derivative will be discussed further in
Sect. 7.
The combined light curves, folded on the period
P1 = 0.113226533 days
(linear ephemeris), are shown in the upper
panel of Fig. 1. Since it cannot be excluded that the
true period is twice as long, the light curves were also folded on
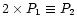 ,
as shown in the upper panel of
Fig. 2. In
the P2 curve the minimum at phase 0.5 appears to be slightly less
deep than the one at phase 0. Moreover, there is no indication of flat
topped maxima as were seen by GB83 and taken by them as an
argument against an ellipticity effect and thus against the longer period.
Therefore, the present results appear to be slightly in favor of a true period
twice as long as originally assumed. In this case the variations are
expected to be due to an elliptical shape of the hotter star (which we
will refer to as the primary regardless of its mass being higher or lower
than that of the cooler star) and - as it turns out, see Sect. 5.2 - to eclipses,
while in the other case they
would be explained as a reflection effect off the illuminated face of the
less luminous star. Evidently, this has a tremendous bearing on any model
of MT Ser. We will not try to decide the question of the true period based on
a visual inspection of the light curves alone. We will rather
try to find solutions using light curve synthesis for both cases.
,
as shown in the upper panel of
Fig. 2. In
the P2 curve the minimum at phase 0.5 appears to be slightly less
deep than the one at phase 0. Moreover, there is no indication of flat
topped maxima as were seen by GB83 and taken by them as an
argument against an ellipticity effect and thus against the longer period.
Therefore, the present results appear to be slightly in favor of a true period
twice as long as originally assumed. In this case the variations are
expected to be due to an elliptical shape of the hotter star (which we
will refer to as the primary regardless of its mass being higher or lower
than that of the cooler star) and - as it turns out, see Sect. 5.2 - to eclipses,
while in the other case they
would be explained as a reflection effect off the illuminated face of the
less luminous star. Evidently, this has a tremendous bearing on any model
of MT Ser. We will not try to decide the question of the true period based on
a visual inspection of the light curves alone. We will rather
try to find solutions using light curve synthesis for both cases.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Bruch-f1.ps}\end{figure}](/articles/aa/full/2001/39/aah2736/Timg25.gif) |
Figure 1:
Top: Light curve of MT Ser folded on the nominal
orbital period,
P=P1, (dots) and two different model light curves
(solid and dashed lines). Centre and bottom:
O-C curve between the observations and the model light
curves; for details, see text. |


Up: An analysis of the MT Serpentis
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Bruch-f1.ps}\end{figure}](/articles/aa/full/2001/39/aah2736/Timg25.gif)