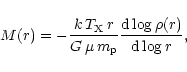 |
(1) |
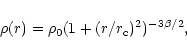 |
(2) |
Furthermore, if we have the density contrast
![]() (where
(where
![]() is the mean density
inside the radius r and
is the mean density
inside the radius r and
![]() is the critical density at the
redshift of the cluster) then we can define
is the critical density at the
redshift of the cluster) then we can define
![]() as
as
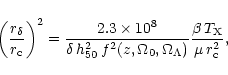 |
(4) |
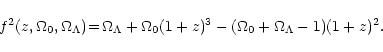 |
(5) |
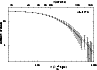 |
Figure 9:
X-ray brightness profile (IPC data with error bars),
obtained with the STSDAS/IRAF task ellipse; the continuous
line is the best-fit |
In Fig. 10 we show the cluster mass profile computed with the
virial mass estimator (VME) which, as discussed by Aceves & Perea (1999),
gives less biased mass estimates when the system is not completely
sampled. These authors also show that the VME overestimates the real mass
by no more than 20% at small radii, being more reliable at larger
apertures. The error bars in Fig. 10 are 1-![]() standard deviations
computed using the bootstrap method. The VME assumes, of course, that the
system is virialized. In general, the presence of substructures or
large-scale flows tend to increase the velocity dispersion of the galaxies,
leading to an overestimation of the mass of the system.
standard deviations
computed using the bootstrap method. The VME assumes, of course, that the
system is virialized. In general, the presence of substructures or
large-scale flows tend to increase the velocity dispersion of the galaxies,
leading to an overestimation of the mass of the system.
The VME of Abell 970, within
1.2 h50-1 Mpc, is
![]() ,
where the error, as before, was computed with
the bootstrap method. Note that, for a virialized cluster, these are lower
limits for the mass, since we have velocities only for the central region
of the system. Indeed, assuming a relation between virial radius and
velocity dispersion similar to that adopted by Girardi et al. (1998), we
estimate that
,
where the error, as before, was computed with
the bootstrap method. Note that, for a virialized cluster, these are lower
limits for the mass, since we have velocities only for the central region
of the system. Indeed, assuming a relation between virial radius and
velocity dispersion similar to that adopted by Girardi et al. (1998), we
estimate that
![]() Mpc, while the velocities have
been measured within a region of radius
Mpc, while the velocities have
been measured within a region of radius ![]() 1.2 h50-1 Mpc.
1.2 h50-1 Mpc.
Figure 10 also displays the run of the total bj luminosity of
the cluster (up to
bj = 19.75). Considering the VME masses, we find that
the mass-luminosity ratio ranges from 1360
![]() at the cluster central region, to
at the cluster central region, to ![]() 450
450
![]() at the largest aperture.
at the largest aperture.
The mass profile derived from the X-ray emission is also presented in
Fig. 10. The VME masses are in excess of the X-ray mass
estimates by large factors, ranging from ![]() 16 for the central
apertures, to about 4 at
16 for the central
apertures, to about 4 at ![]() 1.3
h50-1 Mpc aperture, which
encompasses the whole velocity sample. These factors are well above the
uncertainties discussed above for virialized clusters. In fact, the
dynamical mass determined by the X-ray emission at radius
1.3
h50-1 Mpc aperture, which
encompasses the whole velocity sample. These factors are well above the
uncertainties discussed above for virialized clusters. In fact, the
dynamical mass determined by the X-ray emission at radius
![]() depends essentially on the temperature and the asymptotic slope of the
gas density. Both are poorly determined with the available data; it is then
possible that one of them (or both) are under-estimated, which implies that
we under-estimate the dynamical X-ray mass. For instance, if
depends essentially on the temperature and the asymptotic slope of the
gas density. Both are poorly determined with the available data; it is then
possible that one of them (or both) are under-estimated, which implies that
we under-estimate the dynamical X-ray mass. For instance, if ![]() is as
high as 0.70 and
is as
high as 0.70 and
![]() (cf. the error bars in Table 2), then the
dynamical X-ray mass would be twice the estimated value, i.e.,
M(r=1.2 h50-1 Mpc
(cf. the error bars in Table 2), then the
dynamical X-ray mass would be twice the estimated value, i.e.,
M(r=1.2 h50-1 Mpc
![]() .
On the other hand,
the presence of a substructure associated with the cluster brightest galaxy,
as well as the mean velocity gradient, may be an indication of
non-virialization and, consequently, the VME may be largely overestimated.
.
On the other hand,
the presence of a substructure associated with the cluster brightest galaxy,
as well as the mean velocity gradient, may be an indication of
non-virialization and, consequently, the VME may be largely overestimated.
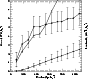 |
Figure 10: Cluster optical masses (circles and dotted lines), X-ray masses (squares and dot-dashed lines) and luminosities (triangles and dashed lines). |
Copyright ESO 2001