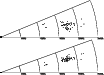
 |
Figure 5:
Wedge velocity diagram in right ascension
(up), and declination (down) for the measured galaxies in Abell 970 with
radial velocities smaller than 25000
|
Our sample contains 69 velocities in the direction of Abell 970. Figure 5 shows a wedge velocity diagram in the direction of the cluster in right ascension (up) and declination (down), and indicates that most of the velocities are between 15000 and 20000 kms-1. A histogram of the velocity distribution is displayed in Fig. 6. In this section we will discuss the velocity distribution, looking for non-equilibrium effects.
 |
Figure 5:
Wedge velocity diagram in right ascension
(up), and declination (down) for the measured galaxies in Abell 970 with
radial velocities smaller than 25000
|
Since the usual recursive ![]() -clipping (Yahil & Vidal 1977) failed to
simultaneously remove the low (
-clipping (Yahil & Vidal 1977) failed to
simultaneously remove the low (
![]() )
and high velocity
(
)
and high velocity
(
![]() )
tails of the distribution, we decided to analyse the
radial velocity distribution of the cluster by constructing four different
data samples to which we applied several statistical tests in order to
assess the normality of their parent distributions. These samples are:
A, comprising all galaxies within
)
tails of the distribution, we decided to analyse the
radial velocity distribution of the cluster by constructing four different
data samples to which we applied several statistical tests in order to
assess the normality of their parent distributions. These samples are:
A, comprising all galaxies within
![]() ;
B, which
is identical to sample A except that the high- and low-velocity tails have
been removed, thus covering the range
;
B, which
is identical to sample A except that the high- and low-velocity tails have
been removed, thus covering the range
![]() ;
C, which is similar to sample B added with the high-velocity tail, that is
;
C, which is similar to sample B added with the high-velocity tail, that is
![]() ;
D, comprising only galaxies in the range
;
D, comprising only galaxies in the range
![]() :
this sample has been considered in view of a
significant gap in the data occurring at
:
this sample has been considered in view of a
significant gap in the data occurring at
![]() (see below).
(see below).
The analysis was made using the ROSTAT statistical package (Beers et al. 1990; Bird & Beers 1993), which proposes various statistical tests based on the empirical distributions of samples. We roughly distinguish 3 categories of normality tests among those included in the ROSTAT package. The first one contains the so-called omnibus tests, which try to quantify the overall deviation of the velocity distribution from a Gaussian, such as the Cramer von-Mises W2 test, the Watson U2 test and the Anderson-Darling A2 test (see Beers et al. 1991, for references). The Kolmogorof-Smirnov (KS) test, which directly calculates the consistency of the observed distribution with a Gaussian, may also be included in this class of tests. The second group of tests are devised to measure the shape of the outskirts of the distribution, such as the kurtosis test (the B2 test) and its robust counterpart, the Tail Index (TI) test (see Bird & Beers 1993, for a discussion), or to test its tail population, such as the a and the W tests, which are most sensitive to the tail of the underlying populations and the u test, which is sensitive to contamination by extreme values (see Yahil & Vidal 1977, for a discussion on these tests). Finally, there are tests which measure the asymmetry of the distribution: the skewness test (B1 test) and its robust version, the Asymmetry Index (AI) test (Bird & Beers 1993). For each of these tests, ROSTAT computes its statistics as well as their associated probabilities p.
The ROSTAT package also provides two statistical tests helping to identify
kinematical substructures in the velocity distributions. These are the gap
analysis (Wainer & Shacht 1978) and the Dip test unimodality (Hartigan &
Hartigan 1985). The Dip test compares the observed distribution against an
uniform one and as so is a conservative test for the unimodality of sample.
The gap analysis estimates the probability that a gap of a given size and
location, between the ordered velocities, may be produced by random sampling
from a Gaussian population. A gap is considered significant if this
probability is less than 0.03. As mentioned above, our radial velocity
sample shows a significant gap at
![]() .
This could be an
indication that the distribution is bimodal. However, the Dip test failed to
reject the unimodality at significance levels better than 10% for any of
the samples.
.
This could be an
indication that the distribution is bimodal. However, the Dip test failed to
reject the unimodality at significance levels better than 10% for any of
the samples.
In Table 3 we list, for each of the samples described above, the values of the statistics and the associated probabilities, p, for the tests discussed above. The B1 and B2 tests were discarded in favour of their robust versions, the AI and the TI tests. Moreover, because the results of the omnibus tests systematically agreed with the KS test, only the results for this last test have been quoted.
| Sample | N | a | p(a) | u | p(u) | W | p(W) |
|
AI |
|
TI |
|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | ||
| A | 65 | 0.639 | 0.01 | 5.005 | 0.838 | 0.01 | 0.01 | 0.069 | 1.292 | 0.05 | ||
| B | 56 | 0.780 | 3.777 | 0.02 | 0.954 | 0.06 | 0.081 | 1.080 | ||||
| C | 59 | 0.711 | 0.01 | 4.730 | 0.881 | 0.01 | 0.01 | 1.057 | 0.04 | 1.273 | 0.05 | |
| D | 48 | 0.829 | 3.403 | 0.01 | 0.940 | 0.02 | -0.514 | 1.015 |
As can be seen from this Table, the normality hypothesis is rejected for
samples A and C at significance levels better than 3% for all the
statistical tests, except the u test. The values of the statistics of
the a and W tests, as well as the TI values, indicate long-tailed
underlying distributions, with sample C being significantly skewed
towards high velocities, a consequence of removing the low-velocity tail
from sample A. Removing both tails of sample A produces sample B,
which seems nearly consistent with normality, as indicated by most of the
tests. Although both the u and the W tests reject normality at high
significance levels for this sample, their results seem contradictory, for
the u statistics suggests a cutoff of the underlying distribution whereas
the W statistics indicates it is long tailed. Notice that both the AI and
TI tests are consistent with a normal underlying distribution for sample B. Very similar results were also obtained for sample D, but now the
distribution seems slightly, but not significantly, skewed towards low
velocities (
![]() ). This is not unexpected for, even if
the marginal indication of bimodality of the distribution given by the gap
analysis were confirmed, there would be no way, at this level of analysis,
to disentangle galaxies belonging to one or to the other underlying
distributions, that is, to B or D. Since the Dip statistics failed to
reject unimodality for any of the samples, we will not consider this
possibility for now, adopting sample B as representative of the radial
velocity distribution of the cluster. We will return to this point at
the end of this section.
). This is not unexpected for, even if
the marginal indication of bimodality of the distribution given by the gap
analysis were confirmed, there would be no way, at this level of analysis,
to disentangle galaxies belonging to one or to the other underlying
distributions, that is, to B or D. Since the Dip statistics failed to
reject unimodality for any of the samples, we will not consider this
possibility for now, adopting sample B as representative of the radial
velocity distribution of the cluster. We will return to this point at
the end of this section.
We will thus assume that the cluster galaxies have radial velocities in the
range between ![]() and
and
![]() .
It is interesting to note that a
low-velocity tail at
.
It is interesting to note that a
low-velocity tail at
![]() ,
similar to the one found here, also
affected the velocity distribution of the cluster Abell 979 (Proust et al.
1995), which is the nearest neighbour cluster of Abell 970 (at about
,
similar to the one found here, also
affected the velocity distribution of the cluster Abell 979 (Proust et al.
1995), which is the nearest neighbour cluster of Abell 970 (at about
![]() NE from its centre), both belonging to the same supercluster. This
suggests the existence of a large foreground structure projected in this
region of the sky.
NE from its centre), both belonging to the same supercluster. This
suggests the existence of a large foreground structure projected in this
region of the sky.
Considering only the 56 galaxies within this velocity range, the cluster
mean velocity is
![]() (corresponding to
z =
0.0587)
(corresponding to
z =
0.0587)![]() . For comparison,
the radial velocity of the E/D galaxy located at the centre of main cluster
is
. For comparison,
the radial velocity of the E/D galaxy located at the centre of main cluster
is
![]() ,
near that of the whole cluster, as should be expected
if this is the dominant cluster galaxy. The cluster velocity dispersion,
corrected following Danese et al. (1980) is
,
near that of the whole cluster, as should be expected
if this is the dominant cluster galaxy. The cluster velocity dispersion,
corrected following Danese et al. (1980) is
![]() (at a confidence level of 68%).
Figure 6 presents the radial velocity distribution of the
cluster galaxies, as well as a Gaussian curve with the same mean velocity
and dispersion observed for these galaxies. Note that this value of
(at a confidence level of 68%).
Figure 6 presents the radial velocity distribution of the
cluster galaxies, as well as a Gaussian curve with the same mean velocity
and dispersion observed for these galaxies. Note that this value of
![]() is well above the value favoured by the
is well above the value favoured by the
![]() relation,
relation, ![]()
![]() (cf. Sect. 4).
(cf. Sect. 4).
If we consider the morphological types, the mean velocities and corrected
velocity dispersions are:
![]() and
and
![]() for E + S0 galaxies (35 objects), and
for E + S0 galaxies (35 objects), and
![]() and
and
![]() for S +
I galaxies (19 objects). Hence, contrary to what is observed in most
clusters, where the velocity dispersion of the late type population tends
to be larger than that of the early type population (Sodré et al. 1989;
Stein 1997; Carlberg et al. 1997; Adami et al. 1998), in Abell 970 we do
not see any significant difference between the velocity dispersion of these
two populations. This might be another indication - besides the presence
of a substructure - that Abell 970 is not in overall dynamical
equilibrium.
for S +
I galaxies (19 objects). Hence, contrary to what is observed in most
clusters, where the velocity dispersion of the late type population tends
to be larger than that of the early type population (Sodré et al. 1989;
Stein 1997; Carlberg et al. 1997; Adami et al. 1998), in Abell 970 we do
not see any significant difference between the velocity dispersion of these
two populations. This might be another indication - besides the presence
of a substructure - that Abell 970 is not in overall dynamical
equilibrium.
Let us now consider again the substructure, as well as the peak of the
galaxy distribution (cf. Fig. 2), taking into account the galaxy
velocities. This analysis will be done with galaxies brighter than
![]() ,
the magnitude where the completeness of our
velocity catalogue in the central regions of the cluster is 75%.
,
the magnitude where the completeness of our
velocity catalogue in the central regions of the cluster is 75%.
The substructure NW of the main cluster has, within a 3 arcmin (
274 h50 kpc) circular region centered on the brightest S0/S galaxy, 7
cluster galaxies brighter than
![]() .
Together, these
galaxies have a low velocity dispersion,
.
Together, these
galaxies have a low velocity dispersion,
![]() ,
more typical of that of loose groups. The mean velocity is
,
more typical of that of loose groups. The mean velocity is
![]() ,
significantly higher than the
overall mean velocity of the cluster. Our velocity catalogue contains 2
galaxies fainter that
,
significantly higher than the
overall mean velocity of the cluster. Our velocity catalogue contains 2
galaxies fainter that
![]() inside this region. Their
inclusion does not significantly change the value of the mean velocity,
although it increases the velocity dispersion to
inside this region. Their
inclusion does not significantly change the value of the mean velocity,
although it increases the velocity dispersion to
![]() ,
a value significantly lower than the
cluster overall velocity dispersion. These results are consistent with the
suggestion that this clump of galaxies forms a loose group infalling
towards the cluster main central condensation. Arguing against the reality
of such a group, we notice that its dominant S0/S galaxy is also the lowest
velocity member, with
,
a value significantly lower than the
cluster overall velocity dispersion. These results are consistent with the
suggestion that this clump of galaxies forms a loose group infalling
towards the cluster main central condensation. Arguing against the reality
of such a group, we notice that its dominant S0/S galaxy is also the lowest
velocity member, with
![]() ,
but this is not statistically
significant.
,
but this is not statistically
significant.
The central cluster condensation has a N-S elongation (see
Fig. 2). A closer examination of the galaxy distribution
indicates that this region is dominated by two small clumps of galaxies,
which we will denote by A and B (see also Fig. 7 below).
Considering circular regions of 1 arcmin (![]()
![]() ), the central
clump, A, is tightly concentrated around the E/D galaxy, having 6 galaxies
brighter than
), the central
clump, A, is tightly concentrated around the E/D galaxy, having 6 galaxies
brighter than
![]() with
with
![]() ,
and a
dispersion
,
and a
dispersion
![]() .
The other clump, B, is about 1.5 arcmin NW of
clump A and is more sparse, with only 4 galaxies, of which 3 are tightly
packed in velocity space with velocity dispersion
.
The other clump, B, is about 1.5 arcmin NW of
clump A and is more sparse, with only 4 galaxies, of which 3 are tightly
packed in velocity space with velocity dispersion
![]() and
mean velocity
and
mean velocity
![]() .
The fourth galaxy that is,
apparently, a member of this clump has, however, a very discrepant radial
velocity,
.
The fourth galaxy that is,
apparently, a member of this clump has, however, a very discrepant radial
velocity,
![]() .
Since it is not apparent in Fig. 2, it
is not clear if B is a real substructure or a fortuitous projected group of
cluster galaxies.
.
Since it is not apparent in Fig. 2, it
is not clear if B is a real substructure or a fortuitous projected group of
cluster galaxies.
Figures 7 and 8 display, respectively, the adaptive
kernel maps for the mean velocity and the mean velocity dispersion of the
sample of cluster galaxies with measured radial velocities brighter than
![]() .
These maps were calculated from the local kernel
weighted averages, with initial kernel size usually larger - in our case
by a factor of 3, as a compromise between signal-to-noise and spatial
resolution - than the optimal size prescribed by Silverman (1986), as
suggested by Biviano et al. (1996). Significance regions for each map were
obtained by a bootstrap, in a fashion similar to that applied to the
projected density maps.
.
These maps were calculated from the local kernel
weighted averages, with initial kernel size usually larger - in our case
by a factor of 3, as a compromise between signal-to-noise and spatial
resolution - than the optimal size prescribed by Silverman (1986), as
suggested by Biviano et al. (1996). Significance regions for each map were
obtained by a bootstrap, in a fashion similar to that applied to the
projected density maps.
The mean velocity map of Fig. 7 clearly indicates the
existence of a velocity gradient across the field, roughly in the E-W
direction. This occurs because galaxies with
![]() populate
predominantly the East-side of the field. The mean velocity of the NW group
discussed above is consistent with this gradient. Interestingly, this
gradient is also consistent with the general gradient one would obtain by
considering all galaxies of our catalogue with velocities between
populate
predominantly the East-side of the field. The mean velocity of the NW group
discussed above is consistent with this gradient. Interestingly, this
gradient is also consistent with the general gradient one would obtain by
considering all galaxies of our catalogue with velocities between ![]() and
and
![]() ,
suggesting that the cluster may be part of a larger
structure running more or less in the E-W direction within, at least, this
velocity range. In fact a (smaller) velocity gradient, in this same general
direction, is also depicted by the mean redshifts of the supercluster
members (cf. Einasto et al. 1997).
,
suggesting that the cluster may be part of a larger
structure running more or less in the E-W direction within, at least, this
velocity range. In fact a (smaller) velocity gradient, in this same general
direction, is also depicted by the mean redshifts of the supercluster
members (cf. Einasto et al. 1997).
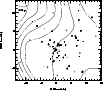 |
Figure 7:
Mean velocity map of the galaxies
kinematically linked to the cluster and brighter than
|
The mean velocity dispersion map displayed in Fig. 8 indicates that there is a radial gradient of the velocity dispersion. This was confirmed by direct calculations of the velocity dispersions within concentric regions centered in the E/D galaxy. Such a gradient is expected if the cluster grows through the capture of low velocity dispersion groups by the central, main galaxy concentration.
The above discussion points to the complexity of the velocity field of
Abell 970. It is possible that the high velocity tail of the cluster velocity
distribution displayed in Fig. 6 may be contaminated by another
component with mean velocity
![]() ,
which
reveals itself trough the peculiarities of its spatial distribution. The
fact that the velocity distribution shows some signs of bimodality, as
pointed out at the beginning of this section, reinforces this suggestion.
If real, this component could be interpreted as a diffuse halo
located at the East-side of the cluster, probably infalling into its dark
matter potential well. If correct, such a scenario may be revealed by
some X-ray emission features typical of gas shocks produced during this
infall.
,
which
reveals itself trough the peculiarities of its spatial distribution. The
fact that the velocity distribution shows some signs of bimodality, as
pointed out at the beginning of this section, reinforces this suggestion.
If real, this component could be interpreted as a diffuse halo
located at the East-side of the cluster, probably infalling into its dark
matter potential well. If correct, such a scenario may be revealed by
some X-ray emission features typical of gas shocks produced during this
infall.
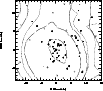 |
Figure 8:
Mean velocity dispersion map of the galaxies
kinematically linked to the cluster and brighter than
|
Copyright ESO 2001