We assume that the stationary, spherically symmetric stellar wind
consists of three components, namely absorbing ions, nonabsorbing
hydrogen atoms and ions,
and electrons, denoted
by subscripts ![]() ,
,
![]() ,
,
![]() ,
respectively.
Each of them is described by a density
,
respectively.
Each of them is described by a density ![]() ,
radial velocity
,
radial velocity
![]() ,
temperature Ta, electrical charge qa=e za(where e is an elementary charge
and za denotes the ionization degree
- may have a non-integer value),
and particle mass ma.
Subscript a stands for
,
temperature Ta, electrical charge qa=e za(where e is an elementary charge
and za denotes the ionization degree
- may have a non-integer value),
and particle mass ma.
Subscript a stands for
![]() .
Contrary to our previous models (KKI), we allow for different
temperature of each component and for radial changes of electrical
charge.
We assume that chemical composition is given by the factor z*, which
is a stellar metallicity relative to the solar value.
.
Contrary to our previous models (KKI), we allow for different
temperature of each component and for radial changes of electrical
charge.
We assume that chemical composition is given by the factor z*, which
is a stellar metallicity relative to the solar value.
In the case of a stationary spherically symmetric stellar wind each component is described by the continuity Eq. (4) in the form of
|
|
(35a) |
where the term Sa accounts for radial change of mass-loss rate of
individual components due to the ionization.
Whereas for
all
types of ions the mass-loss rate is constant through the wind and thus
number of these particles is conserved (
![]() ),
we account for the possibility of variation of electron number via
ionization and recombination.
Because the total electric charge is conserved,
),
we account for the possibility of variation of electron number via
ionization and recombination.
Because the total electric charge is conserved,
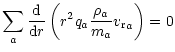 |
|
|
(35b) |
Although inclusion of a term
![]() into the electron continuity
equation does not significantly alter the model, it is important to
obtain well converged model.
into the electron continuity
equation does not significantly alter the model, it is important to
obtain well converged model.
In the case of stationary spherically symmetric stellar wind the momentum
equation Eq. (6) has the form of
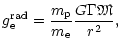 |
(37) |
The radiative acceleration acting on absorbing ions is taken in the
form of Castor et al. (1975)
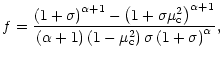 |
(39) |
Constant of friction evaluated using Fokker-Planck approximation (cf.
Burgers 1969) has the following form:
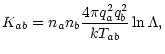 |
(40) |
| (41) |
![$\displaystyle \ln\Lambda=
\ln\left[\frac{3k{T}_{{\rm e}}}{e^2}\left(\frac{k{T}_{{\rm e}}}{4\pi n e^2}\right)^{1/2}\right],$](/articles/aa/full/2001/37/aa1524/img104.gif) |
(42) |
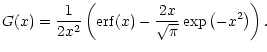 |
(43) |
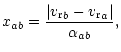 |
(44) |
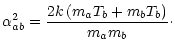 |
(45) |
Energy Eq. (9) in the case of a stationary,
spherically symmetric multicomponent flow has the form of (cf. Burgers
1969)
There are two sources of radiative heating/cooling. First source are bound-free and free-free transitions and the second is Gayley-Owocki heating/cooling.
Bound-free and free-free transitions (which will be called "classical''
radiative transitions) deposit energy directly on electrons.
Therefore, this classical radiative energy term should be considered in an
electron energy equation.
We decided to estimate the radiative heating/cooling term
![]() using two mechanisms only, hydrogen Lyman
bound-free and free-free transitions.
The detailed form of heating and cooling in the above mentioned
transitions is nearly the same as in KKI and will not be repeated here
(see also Kubát et al. 1999).
The only difference is that the temperature in these equations is now
the electron temperature.
using two mechanisms only, hydrogen Lyman
bound-free and free-free transitions.
The detailed form of heating and cooling in the above mentioned
transitions is nearly the same as in KKI and will not be repeated here
(see also Kubát et al. 1999).
The only difference is that the temperature in these equations is now
the electron temperature.
![]() at the base of the wind is taken as an emergent
radiation from a spherically symmetric static hydrogen model
atmosphere for a corresponding stellar type (Kubát 2001).
at the base of the wind is taken as an emergent
radiation from a spherically symmetric static hydrogen model
atmosphere for a corresponding stellar type (Kubát 2001).
Contrary to bound-free and free-free transitions Gayley-Owocki heating/cooling
deposits energy directly to absorbing ions.
GO heating/cooling term has the following form (GO, Eq. (32))
The equation for charge separation electric field can be obtained
directly from the third Maxwell equation, which in the case of spherical
symmetry can be written as
The ionization structure of stellar wind should be derived using time
consuming NLTE calculations (e.g. Pauldrach et al. 1994).
Because we want to determine only a mean charge of selected elements,
we use a simpler approximate method.
As described by Mihalas (1978, Eq. (5.46) therein), the ionization
equilibrium in stellar winds can be approximated by
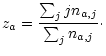 |
(50) |
We write model equations in a simplified form, where we explicitly write
only terms containing derivatives of individual variables and other
terms are included into the terms ![]() .
Thus, the continuity Eqs. (35a), (35b) are
.
Thus, the continuity Eqs. (35a), (35b) are
|
|
(51a) |
In the electron continuity Eq. (35b) we neglected the
derivatives of ionic charge because their contribution to electron
continuity equation is only marginal.
However, inclusion of such term influences critical point and regularity
conditions for electrons only, which will not be used (see bellow).
Similarly we can rewrite momentum Eq. (36). In the momentum equations of absorbing ions we shall linearize a term containing the velocity gradient. Note that because model equations are not quasi-linear (i.e. linear with respect to the derivatives of the independent variables), the mathematically more correct method would employ some form of transformation to the quasi-linear form (cf. Courant & Hilbert 1962). However, because the results are essentially the same in this case, we present analysis of critical points in a simplified form. Thus, momentum equations are
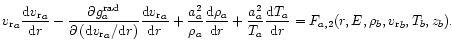 |
(51b) |
Similarly, due to the dependence of the Doppler term on the velocity
gradient (in the Sobolev approximation) we shall write energy equations
in the form of
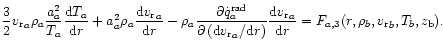 |
(51c) |
The system of equations is closed by the equation for charge separation
electric field, which has a simple form,
![]() (51d)
(51d)
The system of Eq. (51) can be simplified by inserting
the derivatives of density from the Eq. (51a) and derivatives
of temperature (51c) into the momentum Eq. (51b).
We obtain modified linearized
momentum equations
For the passive plasma the critical point condition (52)
has a simple form
Critical point condition Eq. (52) for absorbing ions has form
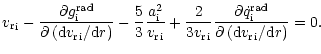 |
(55) |
![$\displaystyle \sum_a \rho_a \frac{{\rm d} { {v_{\rm r}}}_a}{{\rm d}r} \left[{ {...
... i}} /{\rm d}r\right)}\right]= \sum_a F_{a}(r,E,\rho_b, {v_{\rm r}}_b,T_b,z_b).$](/articles/aa/full/2001/37/aa1524/img138.gif) |
(56) |
The last critical point condition for electrons has again a very simple
form
We assume that the flow at the inner boundary is in radiative equilibrium and that the boundary temperature of all components is the same, thus, we write boundary condition for temperatures in the form of
|
|
(60a) |
|
|
(60b) |
Boundary values of ionic charges can be directly obtained from the
condition of ionization equilibrium (49).
Conditions (54), (57) can be generally used to fix the boundary values of model quantities. However, inclusion of two inner conditions directly into model equations sometimes leads to numerical problems. Therefore, we use a more secure method, which gives essentially the same results.
We start to calculate our models at the passive plasma critical point.
Consequently, the boundary condition for the passive plasma velocity is
the critical point condition
Eq. (53).
Boundary condition for
the velocity of absorbing ions
may be obtained from the passive plasma regularity condition
Eq. (54).
Because we suppose equal boundary temperatures of each component
Eq. (60a), the regularity condition may be simplified
The boundary value of electron velocity
is chosen
to fulfil the electron regularity condition Eq. (59) at the
electron critical point Eq. (58).
As was already mentioned, this condition is approximately satisfied
if the zero current condition
We write the boundary condition for the passive plasma density in the
same form as in KKI,
The boundary value of ionic density is determined
numerically to obtain CAK-type solution (see Sect. 3.9).
Boundary electron density is calculated from the condition of
quasi-neutrality
Because we have no critical point condition to determine the intensity of the electric field at the stellar surface, we used the condition of neutrality, which simply sets the gradient of the electric field at the stellar surface to zero (cf. Eq. (48)).
We apply the Henyey method (Henyey et al. 1964), which is a
modification of the well-known Newton-Raphson method to solve equations
described here together with the appropriate boundary conditions.
We use essentially the same method as KKI, except that the vector of
variables at each grid point d has the form of
| (65) |
| (66) |
First of all we search for the boundary density
![]() .
We compute several wind models (each of them is a result of several
Newton-Raphson iterative steps) for the region near the star for
different values of
.
We compute several wind models (each of them is a result of several
Newton-Raphson iterative steps) for the region near the star for
different values of ![]() (for more details see KK0, KKI).
We select such value of
(for more details see KK0, KKI).
We select such value of ![]() which allows wind model to pass
smoothly through the point defined by the Eq. (57) and to
obtain CAK-type solution.
After the appropriate value of
which allows wind model to pass
smoothly through the point defined by the Eq. (57) and to
obtain CAK-type solution.
After the appropriate value of ![]() is chosen, we compute the wind
model downstream of the point defined by the Eq. (57) again using
several Newton-Raphson iterative steps.
is chosen, we compute the wind
model downstream of the point defined by the Eq. (57) again using
several Newton-Raphson iterative steps.
The detailed method of calculation of Gayley-Owocki heating/cooling term is given in Appendix A.
Copyright ESO 2001