

Up: Multicomponent radiatively driven stellar
Subsections
The procedure of the derivation of the hydrodynamic equations from the
Boltzmann equation for particle distribution function Fs of the
particle s is thoroughly described in a number of textbooks.
However, it is commonly assumed that the Boltzmann equation can be
written in the form (we use the Einstein summation law)
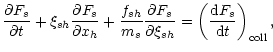 |
|
|
(1) |
i.e. it is assumed that the force fs is
independent of velocity, which is acceptable when we consider
gravitational or electrical forces.
However, the latter assumption is not valid for the case of a wind
driven by radiative force coming from line absorption, which is strongly
dependent on a velocity gradient.
Therefore, we rederive here hydrodynamic equations without an
assumption of the force independent of velocity.
In this case, the Boltzmann equation for the one-particle
distribution function Fs of particles of type s is written as
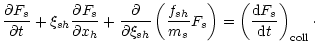 |
|
|
(2) |
Here 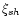 (h=1,2,3) are the velocity components of
individual particles of a type s with mass ms, and fsh are the
components of an external force acting on them.
The right-hand side term expresses the effect of collisions.
By a definition, the integral of the distribution function over the
velocity space is a number density ns of s-particles,
(h=1,2,3) are the velocity components of
individual particles of a type s with mass ms, and fsh are the
components of an external force acting on them.
The right-hand side term expresses the effect of collisions.
By a definition, the integral of the distribution function over the
velocity space is a number density ns of s-particles,
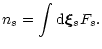 |
|
|
(3) |
Now, the usual way to obtain hydrodynamic equations is the following.
One multiplies the Boltzmann Eq. (2) by multipliers
ms,
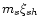 and
and
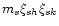 and integrates it over the velocity space.
For the discussion of the role of velocity dependent force in the
Boltzmann equation we confine us to the left-hand side of the Boltzmann
equation.
The right-hand side (i.e. the collisional term) remains unaffected by
the presence of such forces,
so we assume in this section that the gas is collisionless, i.e. that
the right hand side of the Boltzmann equation is zero.
and integrates it over the velocity space.
For the discussion of the role of velocity dependent force in the
Boltzmann equation we confine us to the left-hand side of the Boltzmann
equation.
The right-hand side (i.e. the collisional term) remains unaffected by
the presence of such forces,
so we assume in this section that the gas is collisionless, i.e. that
the right hand side of the Boltzmann equation is zero.
Multiplying the Boltzmann Eq. (2) by ms and
integrating over the velocity space we obtain the continuity equation
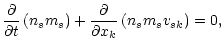 |
|
|
(4) |
where vsk are the components of the mean velocity of particles s,
and
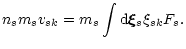 |
|
|
(5) |
Here, the force term disappeared through integration by parts and the
collisional term is also zero.
Apparently, velocity-dependent external force does not change the
continuity equation.
Multiplying the Boltzmann Eq. (2) by
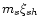 and
integrating over the velocity space we obtain momentum equation
and
integrating over the velocity space we obtain momentum equation
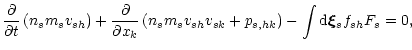 |
|
|
(6) |
where ps,hk are the components of the momentum transfer tensor, and
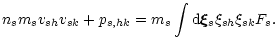 |
|
|
(7) |
Again, the velocity term was integrated by parts. Note, that due to the
velocity dependence of the external force the term containing fshcannot be moved in front of the integral.
Multiplying the Boltzmann Eq. (2) by
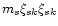 and integrating over the velocity space we obtain energy equation
and integrating over the velocity space we obtain energy equation
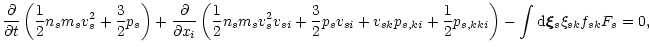 |
|
|
(8) |
where
ps=1/3 ps,kk is the scalar hydrostatic pressure and
the last term was simplified using integration by parts.
The equation for the temperature can be derived by subtracting the
momentum Eq. (6) dot-multiplied by vsh from
the Eq. (8),
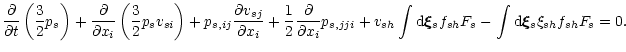 |
|
|
(9) |
Note that the last two terms cancel if the force does not depend on the
velocity.
For this "standard'' case the external force does not give any
contribution to net heating.
Let us explore now the last term on the left hand side of Eq. (9) for the case of the force caused by absorption of
radiation in spectral lines.
This force depends on particle velocity through the velocity dependence
of the line absorption coefficient owing to the Doppler effect.
Therefore, Gayley & Owocki (1994, hereafter GO) termed the
heating effect by Doppler heating, but terming it
Gayley-Owocki heating (or GO heating in the abbreviated form)
might be more appropriate.
Let us denote the heating term in the comoving
fluid-frame as
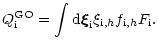 |
|
|
(10) |
Here the index
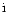 stands for "absorbing ions''.
Although this term is written in the comoving fluid-frame, the same
expression holds in the non-relativistic case also in the
observer frame.
Let us assume complete redistribution and an angle independent
opacity and emissivity in the atomic frame.
However, the emissivity in the comoving fluid-frame is generally angle
dependent due to the Doppler effect.
Therefore, the radiative force acting on an atom in the
comoving fluid-frame is
stands for "absorbing ions''.
Although this term is written in the comoving fluid-frame, the same
expression holds in the non-relativistic case also in the
observer frame.
Let us assume complete redistribution and an angle independent
opacity and emissivity in the atomic frame.
However, the emissivity in the comoving fluid-frame is generally angle
dependent due to the Doppler effect.
Therefore, the radiative force acting on an atom in the
comoving fluid-frame is
![$\displaystyle f_{{\rm i},h} = \frac{m_{\rm i}}{c} \int_0^\infty {\rm d} \nu
\oi...
...ga \left[\kappa(\vec{n},\nu) I(\vec{n},\nu) - \epsilon(\vec{n},\nu)\right]
n_h,$](/articles/aa/full/2001/37/aa1524/img31.gif) |
|
|
(11) |
where
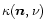 and
and
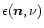 are the
absorption and emission coefficients per unit mass, which can be
expressed as
are the
absorption and emission coefficients per unit mass, which can be
expressed as
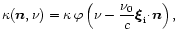 |
|
|
(12a) |
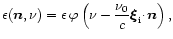 |
|
|
(12b) |
where
 is the absorption (emission) profile in the atomic
frame.
After some rearrangement we obtain
is the absorption (emission) profile in the atomic
frame.
After some rearrangement we obtain
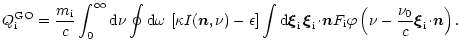 |
|
|
(13) |
If for the calculation of the last integral we choose one of the
velocity axes parallel to the direction of n, then the
integrals over other two axes vanishes (we integrate odd function) and
the Gayley-Owocki heating formula becomes
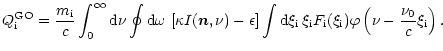 |
|
|
(14) |
where
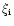 is a velocity component in the direction of
is a velocity component in the direction of
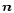 .
If we rewrite photon-line-of-sight velocity component as
.
If we rewrite photon-line-of-sight velocity component as
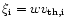 and use frequency displacement from the line center in Doppler units
and use frequency displacement from the line center in Doppler units
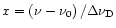 ,
then the GO heating takes the form
,
then the GO heating takes the form
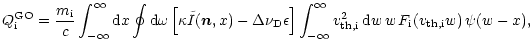 |
|
|
(15) |
where we introduced the intensity
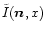 as
as
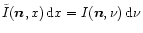 and
the function
and
the function
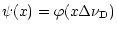 |
|
|
(16) |
is normalized according to Castor (1974) as
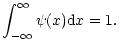 |
|
|
(17) |
Note that the thermal speed
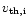 is really ionic because it comes
from the velocity distribution of absorbing ions (shall not be
interchanged with
is really ionic because it comes
from the velocity distribution of absorbing ions (shall not be
interchanged with
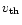 ,
which comes from normalization of force
multipliers).
We neglect absorption in the resonance wings of the profile and
approximated
,
which comes from normalization of force
multipliers).
We neglect absorption in the resonance wings of the profile and
approximated
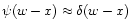 .
Finally,
we assume that the velocity distribution is
given by the Maxwellian velocity distribution,
.
Finally,
we assume that the velocity distribution is
given by the Maxwellian velocity distribution,
The latter assumption was made purely due to simplicity reasons.
Relaxing it could lead to interesting effects especially if
the number of collisions is not sufficient to maintain an equilibrium
(cf., e.g., Scudder 1994; Cranmer 1998).
However, we postpone the analysis of the non-Maxwellian effects to a
future paper.
Thus, the GO heating formula takes the form of
![$\displaystyle {Q}_{{\rm i}}^{{\rm GO}} =
\frac{{m}_{{\rm i}} {n}_{{\rm i}} v_{{...
...\,x \phi(x)
\left[\kappa \tilde I({\vec n},x)-\Delta\nu_{\rm D}\epsilon\right],$](/articles/aa/full/2001/37/aa1524/img52.gif) |
|
|
(18) |
where
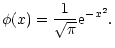 |
|
|
(19) |
Due to the symmetry of the absorption profile (19)
the product 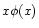 is an odd function and, thus, after integration
over x, vanishes.
This means that in the case of complete redistribution the process of
emission gives no direct contribution to
GO
heating, i.e.
is an odd function and, thus, after integration
over x, vanishes.
This means that in the case of complete redistribution the process of
emission gives no direct contribution to
GO
heating, i.e.
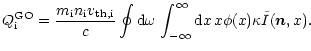 |
|
|
(20) |
In the static medium the product
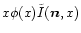 is an odd function of x,
thus, there is no
GO
heating effect in static stellar atmospheres.
In the particular case of a spherically-symmetric stellar wind the
expression for the Gayley-Owocki heating takes the form of
is an odd function of x,
thus, there is no
GO
heating effect in static stellar atmospheres.
In the particular case of a spherically-symmetric stellar wind the
expression for the Gayley-Owocki heating takes the form of
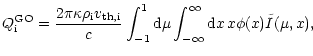 |
|
|
(21) |
where
 ,
which was actually used by GO.
,
which was actually used by GO.
In the case of a two-level atom without continuum the solution of the
transfer equation in the Sobolev approximation is (Rybicki & Hummer
1978; Owocki & Rybicki 1985, GO)
![$\displaystyle \tilde I(\mu,x)=\tilde I_{\rm c}
\left\{\frac{\beta_{\rm c}}{\beta}+\left[D(\mu)-
\frac{\beta_c}{\beta}\right]
{\rm e}^{-\tau_\mu\Phi(x)}\right\},$](/articles/aa/full/2001/37/aa1524/img59.gif) |
|
|
(22) |
where
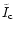 is the core intensity,
is the core intensity,
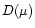 is unity for
is unity for 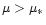 and
zero otherwise (
and
zero otherwise (
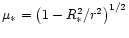 ), core penetration and
escape probabilities are given by
), core penetration and
escape probabilities are given by
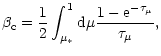 |
|
|
(23) |
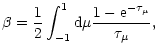 |
|
|
(24) |
respectively, and
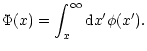 |
|
|
(25) |
The Sobolev optical depth 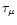 is given by
(Castor 1974; Rybicki & Hummer 1978)
is given by
(Castor 1974; Rybicki & Hummer 1978)
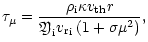 |
|
|
(26) |
where the variable 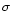 was introduced by Castor (1974)
was introduced by Castor (1974)
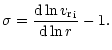 |
|
|
(27) |
Inserting the solution of the transfer Eq. (22) into the
expression for the GO heating Eq. (21) we obtain
![$\displaystyle {Q}_{{\rm i}}^{{\rm GO}} =
\frac{2\pi\kappa{\rho}_{{\rm i}}v_{{\r...
...right]
\int_{-\infty}^{\infty} {\rm d}x\, x \phi(x) {\rm e}^{-\tau_\mu\Phi(x)}.$](/articles/aa/full/2001/37/aa1524/img70.gif) |
|
|
(28) |
The effect of line ensemble is usually described using the concept of a
line-strength distribution function (CAK, Abbott 1982; Puls et al. 2000)
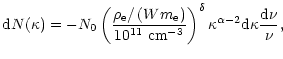 |
|
|
(29) |
where normalization constant N0 is taken in the form of
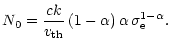 |
|
|
(30) |
The
GO
heating formula for this line ensemble can be obtained by the
integration of the
heating term for one line (Eq. (28)) over
the CAK distribution function Eq. (29).
In this case
it
takes the form of
![$\displaystyle {Q}_{{\rm i}}^{{\rm GO}} = \frac{{\rho}_{{\rm i}}v_{{\rm th}}v_{{...
...right]
\int_{-\infty}^{\infty} {\rm d}x\, x \phi(x) {\rm e}^{-\tau_\mu\Phi(x)},$](/articles/aa/full/2001/37/aa1524/img73.gif) |
|
|
(31) |
where
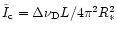 was used.
Finally, applying substitution
was used.
Finally, applying substitution
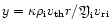 preceding equation becomes
preceding equation becomes
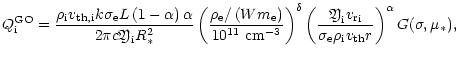 |
|
|
(32) |
where the function
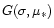 is given by the triple integration
is given by the triple integration
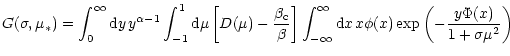 |
|
|
(33) |
and in the integrals for
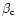 and
and 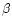 Eqs. (23), (24)
the Sobolev depth shall be computed using
Eqs. (23), (24)
the Sobolev depth shall be computed using
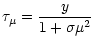 |
|
|
(34) |
instead of Eq. (26).
Contrary to the radiative force formula (Castor 1974) the
GO heating formula depends on the absorption profile.
For the determination of the
GO
heating term we selected Gaussian profile
(which comes from the Maxwellian velocity distribution).


Up: Multicomponent radiatively driven stellar
Copyright ESO 2001
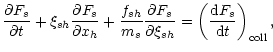
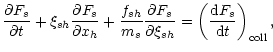
![]() and
integrating over the velocity space we obtain momentum equation
and
integrating over the velocity space we obtain momentum equation
![]() and integrating over the velocity space we obtain energy equation
and integrating over the velocity space we obtain energy equation
![]() is the absorption (emission) profile in the atomic
frame.
After some rearrangement we obtain
is the absorption (emission) profile in the atomic
frame.
After some rearrangement we obtain
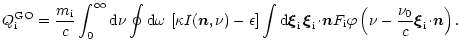
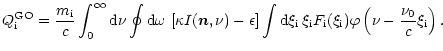
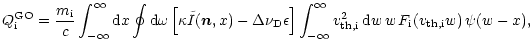
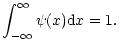
![$\displaystyle {Q}_{{\rm i}}^{{\rm GO}} =
\frac{{m}_{{\rm i}} {n}_{{\rm i}} v_{{...
...\,x \phi(x)
\left[\kappa \tilde I({\vec n},x)-\Delta\nu_{\rm D}\epsilon\right],$](/articles/aa/full/2001/37/aa1524/img52.gif)
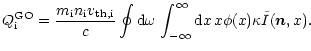
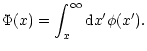
![$\displaystyle {Q}_{{\rm i}}^{{\rm GO}} = \frac{{\rho}_{{\rm i}}v_{{\rm th}}v_{{...
...right]
\int_{-\infty}^{\infty} {\rm d}x\, x \phi(x) {\rm e}^{-\tau_\mu\Phi(x)},$](/articles/aa/full/2001/37/aa1524/img73.gif)