

Up: Orbital decay of satellites
![\begin{figure}
\par\includegraphics[width=10cm,clip]{fgr7.eps}\end{figure}](/articles/aa/full/2001/35/aa1036/Timg202.gif) |
Figure A.1:
A modified distribution nt(a) of satellites in the sample.
Columns (i)-(iv) show the modified distributions which are developed
following the interaction with the corresponding disc models. (The
models are listed in Sect. 3.) The last two columns reflect
the structure of composite models consisting of different regions, as
indicated on top. The evolution of the composite models can be compared
with the case of individual simple models from which they are
constructed. In each graph, line types of the curves reflect different
views of nt(a) profiles (see the text). First, snapshots are shown
with varying time
(top row;
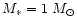 ); second, the fraction of satellites aligned
with the disc is extracted from the whole sample (middle row); third,
the quasi-stationary states are plotted for different ); second, the fraction of satellites aligned
with the disc is extracted from the whole sample (middle row); third,
the quasi-stationary states are plotted for different 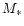 (bottom
row). See the Appendix for exact interpretation of different
rows of graphs.
(bottom
row). See the Appendix for exact interpretation of different
rows of graphs. |
We can expand the results of Sect. 3.2 in slightly more
detail by examining how the modified cluster distribution depends on the
adopted accretion regime and how the quasi-stationary state is
eventually established. There is a qualitative difference from the
simpler case discussed in the main text, because varying surface density
profiles of the disc models (i)-(v) introduce potentially observable
concentrations of satellites at certain radii. Also, it is instructive
to recover in the graphs different influences resulting from orbital
decay, discussed for individual satellites in previous paragraphs
(Sect. 2).
In Fig. A.1, the first four columns correspond to simple models
adopted from our list. In the remaining two columns, the disc consists
of a conjunction of two different models, joined at a given radius: The
model denoted (ii)+(iii) is formed by the inner (ii) and the outer (iii) part
of the gas pressure dominated disc with the transition at
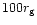 .
Similarly, the model denoted (i)+(iv) is a conjunction of the radiation
pressure dominated disc spreading up to
.
Similarly, the model denoted (i)+(iv) is a conjunction of the radiation
pressure dominated disc spreading up to
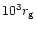 with the outer,
self-gravitating disc (Collin & Huré 1999). The model parameters
determine the final
form of plotted curves in their mutual interplay together with the mass
with the outer,
self-gravitating disc (Collin & Huré 1999). The model parameters
determine the final
form of plotted curves in their mutual interplay together with the mass 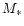 of the cluster members, which remains the
characteristic influencing the efficiency of individual contributions
to the cluster evolution.
of the cluster members, which remains the
characteristic influencing the efficiency of individual contributions
to the cluster evolution.
Given a, the values of nt(a) are distinguished from each other if
a substantial fraction of the satellites are inclined in the plane of the
disc without opening a gap in it. In such a situation the migration is
faster for more massive stars whose number density is then lowered with
respect to low-mass stars. Radial distribution of the satellites is
influenced by the mode of their migration in the disc, and as a
consequence the satellites are transported at different rates
towards the centre. As a result, a wiggle occurs in the nt(a) curve. The
particular value of a where the satellites are accumulated at an
increased rate, forming a ring-type structure, depends on the details of
the model. However, the trend to accumulation at some distance is seen
in various other situations and it leads to a bias in the mass function
of the cluster.
For example, when the model (ii) is considered, the stars proceed under
the regime of density wave excitation in the disc plane. The
critical point (below which the gap would have been opened) lies at too
small distances,
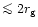 ,
even for the largest considered mass
,
even for the largest considered mass
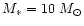 .
Another situation develops in the case (iii)
where the gap is opened below a=5, 150 and
.
Another situation develops in the case (iii)
where the gap is opened below a=5, 150 and
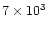 for our
three adopted values of satellite masses. This implies different shapes
of nt(a) for
for our
three adopted values of satellite masses. This implies different shapes
of nt(a) for
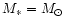 satellites with respect to more massive
ones. Furthermore, in the marginally
unstable disc, i.e. the case (iv), the point above which the gap could
be opened is beyond the outer boundary of the considered region and,
therefore, the distributions nt(a) are sensitive to the mass of the
satellites (most of them are inclined in the disc at this stage).
satellites with respect to more massive
ones. Furthermore, in the marginally
unstable disc, i.e. the case (iv), the point above which the gap could
be opened is beyond the outer boundary of the considered region and,
therefore, the distributions nt(a) are sensitive to the mass of the
satellites (most of them are inclined in the disc at this stage).
In order to maintain clarity of the graphs we omit the curves
corresponding to the model (v). This case is similar to (ii)
except for the fact that the gap opens for all three considered stellar
masses, which makes the case (v) distributions very similar to each
other, quite independent of 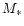 .
.
We could see that simple power-law profiles
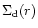 lead to
different distributions with respect to more realistic models, which are
governed by different processes dominating at the corresponding radius.
In discs that are a compound of several parts, the surface density profile
contains several transitions between different regions, and hence it is
more complicated than a simple power-law. The resulting effects on the
boundaries resemble the transitions which we observed previously with
simple discs when the mode of radial migration is changed. A local peak
of nt(a) occurs at radii where the satellites enter the disc region
with slower radial motion, which is the situation of the composite model
(ii)+(iii), or quite on the contrary a dip develops in nt(a) as it
can be seen in the case (i)+(iv).
lead to
different distributions with respect to more realistic models, which are
governed by different processes dominating at the corresponding radius.
In discs that are a compound of several parts, the surface density profile
contains several transitions between different regions, and hence it is
more complicated than a simple power-law. The resulting effects on the
boundaries resemble the transitions which we observed previously with
simple discs when the mode of radial migration is changed. A local peak
of nt(a) occurs at radii where the satellites enter the disc region
with slower radial motion, which is the situation of the composite model
(ii)+(iii), or quite on the contrary a dip develops in nt(a) as it
can be seen in the case (i)+(iv).
We observed that a quasi-stationary distribution nt(a), different
from the initial one, was established below
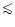
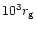 for
rather extended periods of time. However, a decline of n eventually
arrives from large a at final stages when the supply of satellites is
exhausted. The sample is eventually depleted. This can be also seen in
Fig. A.1, the first (top) row, where time evolution is presented
for one solar-mass satellites. Dimensionless times are t=106 (solid
line), 108 (long-dashed), 1010 (short-dashed), 1012(dotted), and 1014 (dash-dotted). See footnote 3 for
time units. The last curve is not visible in all plots because of a very
large t; it can be noticed e.g. in the case (iv) where the evolution is
slow and a fraction of satellites persists above
for
rather extended periods of time. However, a decline of n eventually
arrives from large a at final stages when the supply of satellites is
exhausted. The sample is eventually depleted. This can be also seen in
Fig. A.1, the first (top) row, where time evolution is presented
for one solar-mass satellites. Dimensionless times are t=106 (solid
line), 108 (long-dashed), 1010 (short-dashed), 1012(dotted), and 1014 (dash-dotted). See footnote 3 for
time units. The last curve is not visible in all plots because of a very
large t; it can be noticed e.g. in the case (iv) where the evolution is
slow and a fraction of satellites persists above
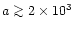 .
.
Complementary to the above-described panels is the second row of graphs
where only a part of nt(a) distribution is plotted, corresponding to
the satellites aligned with the disc. Line styles denote time in the
same manner as in the first row. Naturally, the population of aligned
bodies is less frequent, and hence some curves are missing in
the second row with respect to their matching curves in the first row,
if no satellites are brought to zero inclination.
Finally, the third (bottom) row shows nt(a) profiles taken at
t=1012. At this moment a quasi-stationary state is already
established in the form depending on the mode of satellite-disc
interaction. The profiles are plotted for three different values of the
satellite mass, corresponding to
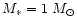 (thick solid
lines),
(thick solid
lines),
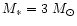 (long-dashed lines), and
(long-dashed lines), and
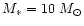 (short-dashed lines). For example, one can check in column (ii) that the
structure of the plot is ruled by the density wave regime and acquires
the corresponding slope. (The initial slope 1/4 is also indicated with
a light dotted line.) The curves
clearly reflect the fact that the orbital decay (9) depends
on
(short-dashed lines). For example, one can check in column (ii) that the
structure of the plot is ruled by the density wave regime and acquires
the corresponding slope. (The initial slope 1/4 is also indicated with
a light dotted line.) The curves
clearly reflect the fact that the orbital decay (9) depends
on 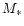 .
.


Up: Orbital decay of satellites
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=10cm,clip]{fgr7.eps}\end{figure}](/articles/aa/full/2001/35/aa1036/Timg202.gif)