

Up: Orbital decay of satellites
Subsections
The satellite body is assumed to cross the disc at supersonic velocity
with a high Mach number,
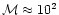 -103. We recall
(Syer et al. 1991; Vokrouhlický & Karas 1993; Zurek et al. 1994) that
passages last a small fraction of the orbital period at the corresponding
radius where they occur, and they can be considered as instantaneous,
repetitive events at which the passing satellite expels from the disc
some amount of material that lies along its trajectory. In terms of
inclination angle i and the disc thickness h, the typical ratio of the
two periods is
-103. We recall
(Syer et al. 1991; Vokrouhlický & Karas 1993; Zurek et al. 1994) that
passages last a small fraction of the orbital period at the corresponding
radius where they occur, and they can be considered as instantaneous,
repetitive events at which the passing satellite expels from the disc
some amount of material that lies along its trajectory. In terms of
inclination angle i and the disc thickness h, the typical ratio of the
two periods is
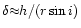 ;
this quantity is assumed
to be less than unity. Hence, for a geometrically thin disc
(
;
this quantity is assumed
to be less than unity. Hence, for a geometrically thin disc
(
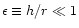 ), its influence upon inclined stellar orbits
can be treated as tiny kicks (impulsive changes of their energy and
momentum) at the points of intersection with the plane of the disc.
This can be translated using the relation for the speed of sound,
), its influence upon inclined stellar orbits
can be treated as tiny kicks (impulsive changes of their energy and
momentum) at the points of intersection with the plane of the disc.
This can be translated using the relation for the speed of sound,
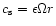 ,
to the claim that the motion across the
disc is indeed supersonic, which is also required for consistency.
Smallness of
,
to the claim that the motion across the
disc is indeed supersonic, which is also required for consistency.
Smallness of 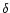 means that the satellite remains outside the disc
for most of its revolution around the centre; naturally this condition
cannot be ensured at final stages when i is very small.
means that the satellite remains outside the disc
for most of its revolution around the centre; naturally this condition
cannot be ensured at final stages when i is very small.
Repetitive collisions lead to the gradual change of the orbiter's velocity
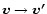 ,
which can be expressed by momentum
conservation (Subr & Karas 1999):
,
which can be expressed by momentum
conservation (Subr & Karas 1999):
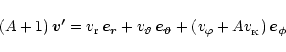 |
(1) |
in spherical coordinates (
 is the disc plane). Here,
is the disc plane). Here,
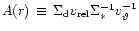 ,
,
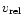 is the relative
speed between the orbiter and the disc matter,
is the relative
speed between the orbiter and the disc matter,
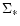 is the
column density characterizing the compactness of the orbiter and defined by
is the
column density characterizing the compactness of the orbiter and defined by
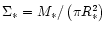 (quantities denoted
by an asterisk refer to the orbiter,
(quantities denoted
by an asterisk refer to the orbiter,
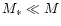 ), and
), and
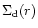 is the disc surface density. Rotation of the disc is
assumed Keplerian,
is the disc surface density. Rotation of the disc is
assumed Keplerian,
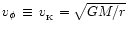 .
.
Let us consider a satellite on an orbit with semi-major axis a,
eccentricity e, inclination i, and longitude 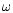 of the
ascending node. Equation (1) implies a set of
equations which can be solved numerically in terms of the orbiter's
osculating elements, while analytical solutions are possible in special
cases (Subr & Karas 1999). As a useful example, we assume a
power-law surface-density distribution in the form
of the
ascending node. Equation (1) implies a set of
equations which can be solved numerically in terms of the orbiter's
osculating elements, while analytical solutions are possible in special
cases (Subr & Karas 1999). As a useful example, we assume a
power-law surface-density distribution in the form
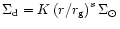 (
(
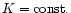 )
and we adopt a perpendicular orientation of the orbit,
)
and we adopt a perpendicular orientation of the orbit,
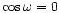 .
We find
.
We find
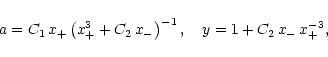 |
(2) |
where
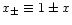 ,
,
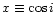 ,
,
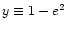 .
Strictly
speaking, this formula concerns only the case of orbits intersecting the
disc at two points with identical radial distances from the center but
it can be used also as an approximation for orbits with arbitrary
orientation. We remark that the relative accuracy
.
Strictly
speaking, this formula concerns only the case of orbits intersecting the
disc at two points with identical radial distances from the center but
it can be used also as an approximation for orbits with arbitrary
orientation. We remark that the relative accuracy
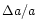 of the
determination of the semi-major axis is better than 15% with reasonable
density profiles (s of the order of unity); numerical computations are
not limited by assumptions about
of the
determination of the semi-major axis is better than 15% with reasonable
density profiles (s of the order of unity); numerical computations are
not limited by assumptions about 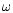 imposed in Eq. (2).
Furthermore, one can write
imposed in Eq. (2).
Furthermore, one can write
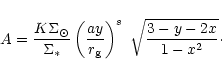 |
(3) |
Integration constants C1,2 are to be determined from initial
values of a=a0, x=x0, and y=y0. Then, the temporal history
is obtained by integrating over the orbital period,
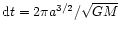 ,
in the form
,
in the form
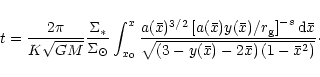 |
(4) |
Here, a factor missing in Eq. (19) of Subr & Karas (1999) is
corrected (no other equations and graphs were affected by that
omission). The orbital decay manifests itself in the gradual decrease of
a, e and i, for which surface density of the disc is the main
factor. The time derivative of the semi-major axis is
![\begin{displaymath}\dot{a}_{\rm {}col}={{\cal B}}y^{-q_4}
\left[\frac{\Sigma_{\...
...t}}\right]^{-1}
\sqrt{\frac{3-y-2x}{y(1-x^2)}} \; (2-x-y) \,,
\end{displaymath}](/articles/aa/full/2001/35/aa1036/img50.gif) |
(5) |
where
![\begin{displaymath}{\cal B}=-BcM_8^{q_1}\mu_{_{\rm {}E}}^{q_2}
\left[\frac{\alpha}{0.1}\right]^{q_3}
\left[\frac{a}{r_{\rm g}}\right]^{-q_4}
\end{displaymath}](/articles/aa/full/2001/35/aa1036/img51.gif) |
(6) |
and
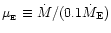 is the accretion rate in units
of Eddington accretion rate (with a 10% efficiency factor introduced).
The factor B and power-law indices
is the accretion rate in units
of Eddington accretion rate (with a 10% efficiency factor introduced).
The factor B and power-law indices
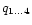 are determined by
details of the particular model adopted to quantify the disc
properties. Table 1 gives the values relevant for different
regions of the standard disc as well as for the gravitationally unstable
outer region (Collin & Huré 1999). Notice that the algebraic
functional form of radial dependencies remains identical in all these
cases (a power-law), and we can use it with convenience also later for
different prescriptions of the satellite-disc encounters.
are determined by
details of the particular model adopted to quantify the disc
properties. Table 1 gives the values relevant for different
regions of the standard disc as well as for the gravitationally unstable
outer region (Collin & Huré 1999). Notice that the algebraic
functional form of radial dependencies remains identical in all these
cases (a power-law), and we can use it with convenience also later for
different prescriptions of the satellite-disc encounters.
Table 1:
Parameters in Eqs. (5), (7) and
(9) describing the orbital decay in the case of different
regimes and for different disc models.
| Regime |
Disc |
B |
q1 |
q2 |
q3 |
q4 |
| col |
(i) |
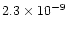 |
0 |
-1 |
-1 |
-1 |
| col |
(ii) |
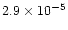 |
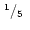 |
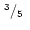 |
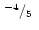 |
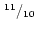 |
| col |
(iii) |
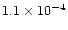 |
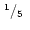 |
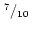 |
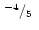 |
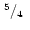 |
| col |
(iv) |
4.05 |
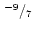 |
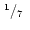 |
0 |
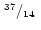 |
| col |
(v) |
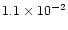 |
-1 |
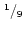 |
0 |
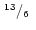 |
| gap |
(i) |
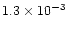 |
0 |
2 |
1 |
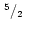 |
| gap |
(ii) |
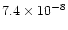 |
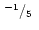 |
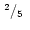 |
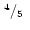 |
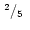 |
| gap |
(iii) |
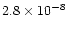 |
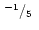 |
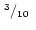 |
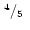 |
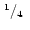 |
| gap |
(iv) |
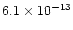 |
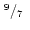 |
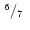 |
0 |
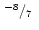 |
| gap |
(v) |
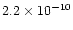 |
1 |
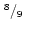 |
0 |
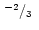 |
| dw |
(i) |
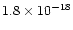 |
0 |
-3 |
-1 |
-5 |
| dw |
(ii) |
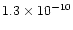 |
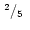 |
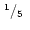 |
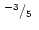 |
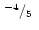 |
| dw |
(iii) |
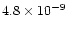 |
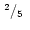 |
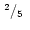 |
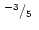 |
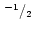 |
| dw |
(iv) |
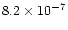 |
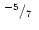 |
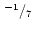 |
0 |
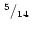 |
| dw |
(v) |
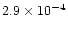 |
-1 |
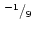 |
0 |
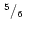 |
Notation used in table.
- Disc models: (i) ... Standard disc with
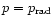 ,
s=3/2; (ii) ... Standard disc
,
s=3/2; (ii) ... Standard disc
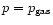 ,
s=-3/5,
electron scattering opacity; (iii) ... The same as (ii) but with
s=-3/4 and free-free opacity; (iv) ... Marginally unstable
self-gravitating disc (solar metallicity, optically thick), s=-15/7;
(v) ... The same as (iv) but for zero metallicity, optically thin
medium, s=-5/3; cf. Sect. 3 for further details.
,
s=-3/5,
electron scattering opacity; (iii) ... The same as (ii) but with
s=-3/4 and free-free opacity; (iv) ... Marginally unstable
self-gravitating disc (solar metallicity, optically thick), s=-15/7;
(v) ... The same as (iv) but for zero metallicity, optically thin
medium, s=-5/3; cf. Sect. 3 for further details.
- Regimes of orbital decay: Orbital decay dominated by
star-disc collisions (col), by gap formation in the disc
(gap), and by density waves (dw), respectively.
As drag is exerted on the satellite body, its orbit becomes circular
and declined in the disc plane. Within this framework, orbital
eccentricity and inclination are expected to reach zero values in the
disc, so that quasi-circular trajectories are relevant near the center.
The orbit evolution is thus reduced to the situation which was addressed
by several people (e.g., King & Done 1993; Takeuchi et al. 1996; Ward
1997; Ostriker 1999) in connection with formation and subsequent
migration of bodies inside the disc. Two basic modes can be
distinguished according to the disc properties and the orbiter mass.
First, a gap is cleared in the disc if the satellite's Roche radius
exceeds the disc thickness,
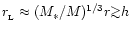 ,
and simultaneously
,
and simultaneously
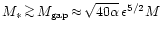 (Lin & Papaloizou 1986). Motion of the satellite is then coupled with
the disc inflow, so that
(Lin & Papaloizou 1986). Motion of the satellite is then coupled with
the disc inflow, so that
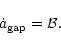 |
(7) |
On the other hand, if the satellite is unable to create the gap, the
gas drag is imposed on it through quasi-spherical accretion.
The resulting radial drift is weaker by a factor
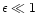 than the drift caused by density-wave excitation (Ward
1986; Artymowicz 1994). Hence, such a satellite migrates inward mainly
due to the latter effect on the time-scale
than the drift caused by density-wave excitation (Ward
1986; Artymowicz 1994). Hence, such a satellite migrates inward mainly
due to the latter effect on the time-scale
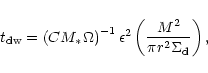 |
(8) |
where C is a dimensionless constant of the order of unity. Using
Eq. (8) and
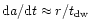 we
obtain
we
obtain
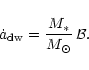 |
(9) |
Substantial differences in the satellite migration are thus introduced
in the model already within this very simplified picture where the
process of satellite sinking is driven by the gas medium. For the
region of the gas pressure dominated standard disc and for a self-gravitating
zero-metalicity model (v), the chance of opening the gap increases with
decreasing radius. The situation is opposite in the case (i) (radiation
pressure dominated) and for the solar-metallicity disc (iv).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fgr2.eps}\end{figure}](/articles/aa/full/2001/35/aa1036/Timg107.gif) |
Figure 1:
Contours of f are plotted as a function of inclination and
eccentricity for the case (ii). Function f(i,e) characterizes the
relative importance of energy losses in Eq. (16).
Values of f are indicated with contour lines. A saddle-type point develops
between two neighbouring contours, f=0.150 and f=0.152, which
are plotted with dashed lines. Its exact location depends on the disc model
but the overall picture remains very similar in other cases, too. |
The orbiting companion emits continuous gravitational radiation whose
waveforms are of particular relevance for gravitational wave searches
from compact binaries in the Milky Way. Possible approaches to their
observational exploration have been discussed by several people (e.g.,
Nakamura et al. 1987; Dhurandhar & Vecchio 2001; Hughes
2001). The average rate of energy loss which the orbiter experiences
via gravitational radiation over one revolution can be written in terms
of orbital parameters (Peters & Mathews 1963),
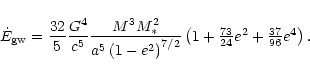 |
(10) |
Corresponding to Eq. (10) are the change of semi-major axis
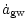 = =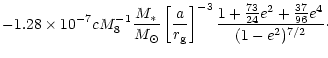 |
(11) |
and the loss of angular momentum
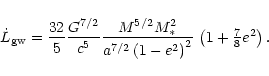 |
(12) |
The above formulae (10)-(12) assume that the
satellite star follows an eccentric orbit in Schwarzschild geometry of
the central massive body. Gravitational radiation losses compete with
those caused by star-disc encounters. We are thus interested in the
relative importance of these mechanisms, which is characterized by the
ratio
![${{\cal R}}_{\rm {}col/gw}=\left[{{\rm d}}a/{{\rm d}}t\right]_{\rm {}col}/
\left[{{\rm d}}a/{{\rm d}}t\right]_{\rm {}gw}$](/articles/aa/full/2001/35/aa1036/img112.gif) :
:
![\begin{displaymath}{{\cal R}}_{\rm {}col/gw}=\frac{5K}{32\pi}\frac{M}{M_\ast}
\...
...ight]^{-1}
\left[\frac{a}{r_{\rm {g}}}\right]^{s+5/2} f(x,e),
\end{displaymath}](/articles/aa/full/2001/35/aa1036/img113.gif) |
(13) |
where, for whichever of the models described by the power-law density
profile,
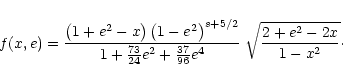 |
(14) |
For the standard thin disc model (i) we obtain
while for a gas pressure dominated disc (ii)
For the model (iii) we find
We show the functional form (14) in Fig. 1 where the factor
f(x,e) determining the dependence of
 on
inclination and eccentricity is plotted for the case (16). In other words, f(x,e) represents that part of
the drag ratio that is independent of the disc medium and the satellite
physical properties; only the two mentioned orbital parameters play a
role here. Typically, for a solar-type star it is only on eccentric
orbits that f becomes small enough to bring
on
inclination and eccentricity is plotted for the case (16). In other words, f(x,e) represents that part of
the drag ratio that is independent of the disc medium and the satellite
physical properties; only the two mentioned orbital parameters play a
role here. Typically, for a solar-type star it is only on eccentric
orbits that f becomes small enough to bring
 below unity. The required eccentricity is rather high, and such a
satellite would be trapped or disrupted directly by the central hole.
Otherwise,
below unity. The required eccentricity is rather high, and such a
satellite would be trapped or disrupted directly by the central hole.
Otherwise,
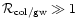 for
for
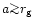 and for
standard values of the disc parameters (
and for
standard values of the disc parameters (
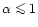 ,
,
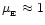 ).
This means that direct hydrodynamical interaction with the disc plays a
dominant role in the orbital evolution of satellites crossing the disc,
unless the medium is extremely rarefied (e.g., an ADAF; Narayan
2000). Notice that the point f(1,0)=0 (i.e. a fully circularized
orbit inclined into the disc plane) is the exception, where the adopted
approximation of instantaneous collisions breaks down.
).
This means that direct hydrodynamical interaction with the disc plays a
dominant role in the orbital evolution of satellites crossing the disc,
unless the medium is extremely rarefied (e.g., an ADAF; Narayan
2000). Notice that the point f(1,0)=0 (i.e. a fully circularized
orbit inclined into the disc plane) is the exception, where the adopted
approximation of instantaneous collisions breaks down.
Analogous to
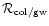 ,
one could explore the relative ratio
of the hydrodynamical versus gravitational radiation losses in other
regimes of the satellite-disc interaction. In this way, the relevant
formulae (those which apply in the course of orbiter evolution) are
,
one could explore the relative ratio
of the hydrodynamical versus gravitational radiation losses in other
regimes of the satellite-disc interaction. In this way, the relevant
formulae (those which apply in the course of orbiter evolution) are
for the inner, radiation pressure dominated disc (i), and
for the middle region (ii). Here, the eccentricity-dependent factor was
omitted upon the finding that orbits are almost circular when inclined in the
plane of the disc. It is evident from Eqs. (13)-(21) that
gravitational radiation can have a visible impact only at small a, especially
when Eq. (18) applies (cp. also Fig. 5 and related discussion
below).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fgr3.eps}\end{figure}](/articles/aa/full/2001/35/aa1036/Timg133.gif) |
Figure 2:
Evolutionary tracks of the satellite are plotted in the
plane semimajor axis a (units of
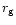 )
versus time (years).
Two very different cases are shown.
a) Left: solar-type satellite ( )
versus time (years).
Two very different cases are shown.
a) Left: solar-type satellite (
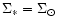 ). The
three curves correspond to different initial eccentricities (from top to
bottom), e0=0, 0.4, and 0.8. Each curve is divided into three segments.
Solid line indicates the period of motion outside the disc (when
collisions occur with large orbital inclination); dashed line
corresponds to density-wave driven motion in the disc; dotted line is
the late stage with gap formation. b) Right: a compact satellite
( ). The
three curves correspond to different initial eccentricities (from top to
bottom), e0=0, 0.4, and 0.8. Each curve is divided into three segments.
Solid line indicates the period of motion outside the disc (when
collisions occur with large orbital inclination); dashed line
corresponds to density-wave driven motion in the disc; dotted line is
the late stage with gap formation. b) Right: a compact satellite
(
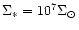 ). Only the first stage is resolved
here. In all cases, a0=100, x0=0. Gravitational radiation
contributes to orbital changes independent of inclination but its impact
is clearly important near the centre, where a decreases rapidly. ). Only the first stage is resolved
here. In all cases, a0=100, x0=0. Gravitational radiation
contributes to orbital changes independent of inclination but its impact
is clearly important near the centre, where a decreases rapidly. |
Now we explore the evolutionary tracks of the satellite in the parameter
space of osculating elements. We start by considering two effects:
gravitational-wave losses in the approximation of Eqs. (10)-(12), and hydrodynamical drag acting on the
satellite according to Eq. (1) twice per
revolution. Dissipation operates with an efficiency depending on the type
of satellite, and it provides a mechanism for the separation of
different types of bodies in the phase space of a cluster.
Typical results of orbit integrations are presented in
Fig. 2. Notice the big difference in time-scales relevant for
non-compact stars (left panel) when compared with compact ones (right
panel). In the former case, hydrodynamical drag is more pronounced. It
gradually changes the orbital plane, while gravitational radiation can be
safely neglected. The satellite sinks in the disc where the impulsive
approximation (5) loses its validity and it is substituted
by motion in the disc plane. Time-scales are generally longer in the
latter, compact satellite case, although gravitational wave emission
speeds up the evolution at very late stages (
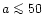 ). For
definiteness, we adopt the disc model (iii) and the condition of
). For
definiteness, we adopt the disc model (iii) and the condition of
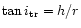 when the transition in the disc occurs. We
checked by modifying the value of
when the transition in the disc occurs. We
checked by modifying the value of
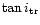 by a factor of 10that the qualitative picture of orbital evolution does not depend on
its exact choice and also that numerical results remain similar.
by a factor of 10that the qualitative picture of orbital evolution does not depend on
its exact choice and also that numerical results remain similar.
For simplification, we ignored the effects of gradual change of the mass
of both the satellite and the central body. Furthermore, we assumed that
the interaction has no effect on the structure of the satellites. This
is a plausible assumption for stars with column densities much larger
than that of the disc, while it is inadequate for giants which must
quickly lose their atmospheres (Armitage et al. 1996). Also,
we did not consider various effects acting on the disc structure (e.g.
torques imposed on it by the dense cluster of stars; Ostriker 1983).
Although all these effects will be important for a complete unified
treatment of accreting black holes in active galactic nuclei, they can
be neglected without losing the main physical effects influencing the
satellite motion in the present simplified scheme.
We note that the significance of direct orbiter's collisions with the
disc material is controlled by a characteristic time-scale
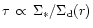 ,
which we expressed in
terms of the orbital decay
,
which we expressed in
terms of the orbital decay 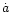 .
Let us recall that dimensionless
parameter characterizing compactness of the orbiter can be introduced in
different ways. While
.
Let us recall that dimensionless
parameter characterizing compactness of the orbiter can be introduced in
different ways. While
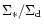 stands directly in
the description of star-disc collisions, the usual factor
stands directly in
the description of star-disc collisions, the usual factor
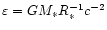 determines the importance of
general relativity effects near the surface of a compact body:
determines the importance of
general relativity effects near the surface of a compact body:
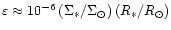 .
We treat motion in the Newtonian regime
and we only take the possibility of the satellite capture into account
by removing the orbiter from a sample if its trajectory plunges too
close to the central mass, below a marginally stable orbit. Another
dimensionless quantity has also been designated as the compactness
parameter when describing accretion onto compact objects,
.
We treat motion in the Newtonian regime
and we only take the possibility of the satellite capture into account
by removing the orbiter from a sample if its trajectory plunges too
close to the central mass, below a marginally stable orbit. Another
dimensionless quantity has also been designated as the compactness
parameter when describing accretion onto compact objects,
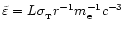 .
It considers the effect of radiation luminosity L acting through a
cross-section
.
It considers the effect of radiation luminosity L acting through a
cross-section
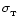 in the medium, however, we can safely
ignore radiation pressure on macroscopic satellites hereafter.
in the medium, however, we can safely
ignore radiation pressure on macroscopic satellites hereafter.
The gradual and monotonic decrease of eccentricity is overlaid with
short-term oscillations if the disc mass is non-negligible
(Vokrouhlický & Karas 1998). Also the satellites' inclination
converges to a somewhat different distribution (instead of a strictly
flattened disc-type system) when two-body gravitational relaxation is
taken into account (Subr 2001; Vilkoviskiy 2001 - preprint). On the
other hand, complementary to the scenario of the satellites grinding
into the disc is the picture of enhanced star formation in the disc
plane, in which case the stars are born with zero inclination (Collin &
Zahn 1999). But these effects, as well as evaporation processes
operating in the cluster, as suggested by various Fokker-Planck
simulations (e.g., Kim et al. 1999), remain beyond the scope of
the present paper.
We could see that different mechanisms (of which we considered
particular examples) affect the orbital motion rather selectively,
depending on the orbiter's size and mass. One thus expects separation of
different objects in the cluster phase space. In order to verify this
expectation we examine in the following paragraph a simple scheme which
captures gradual changes in the structure of the cluster. Such a
discussion is required: indeed, in the absence of sufficient
resolution which would enable tracking of individual stellar paths in
nuclei of other galaxies, one needs to inspect the overall influence on
the members of the cluster, namely, the change of the radial
distribution of the satellites in terms of their number fraction and
average inclination.
Let us note that the accretion flow is supposed to remain undisturbed
by the presence of the embedded cluster. This assumption gives an upper
limit on the total number of stars inside the radius
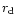 (
(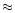
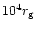 ), and on the fraction of those dragged into the
disc plane in this region. A simple smooth disc can be destroyed,
especially in the process of gap formation (the case of sufficiently
large
), and on the fraction of those dragged into the
disc plane in this region. A simple smooth disc can be destroyed,
especially in the process of gap formation (the case of sufficiently
large 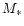 and small h); the models (i) and (v) are particularly
susceptible to the occurence of multiple gaps. Very roughly, if
and small h); the models (i) and (v) are particularly
susceptible to the occurence of multiple gaps. Very roughly, if
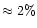 of
the total number of N=104 satellites get aligned with the disc at late times
(a result of our computations for the model (iii)), then their Roche lobes
might cover an area of the order
of
the total number of N=104 satellites get aligned with the disc at late times
(a result of our computations for the model (iii)), then their Roche lobes
might cover an area of the order
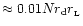 .
This is just comparable with the total disc surface for
.
This is just comparable with the total disc surface for
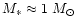 ,
however, recall that
there are more conditions for the gap formation depending on the disc
model. Also, effects of two-body relaxation and of satellite scattering
in the gravitational potential of the disc are expected to decrease
the fraction of aligned bodies when these effects are taken into account.
,
however, recall that
there are more conditions for the gap formation depending on the disc
model. Also, effects of two-body relaxation and of satellite scattering
in the gravitational potential of the disc are expected to decrease
the fraction of aligned bodies when these effects are taken into account.


Up: Orbital decay of satellites
Copyright ESO 2001
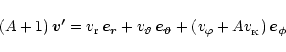
![]() of the
ascending node. Equation (1) implies a set of
equations which can be solved numerically in terms of the orbiter's
osculating elements, while analytical solutions are possible in special
cases (Subr & Karas 1999). As a useful example, we assume a
power-law surface-density distribution in the form
of the
ascending node. Equation (1) implies a set of
equations which can be solved numerically in terms of the orbiter's
osculating elements, while analytical solutions are possible in special
cases (Subr & Karas 1999). As a useful example, we assume a
power-law surface-density distribution in the form
![]() (
(
![]() )
and we adopt a perpendicular orientation of the orbit,
)
and we adopt a perpendicular orientation of the orbit,
![]() .
We find
.
We find
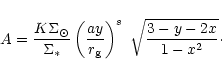
![\begin{displaymath}{\cal B}=-BcM_8^{q_1}\mu_{_{\rm {}E}}^{q_2}
\left[\frac{\alpha}{0.1}\right]^{q_3}
\left[\frac{a}{r_{\rm g}}\right]^{-q_4}
\end{displaymath}](/articles/aa/full/2001/35/aa1036/img51.gif)
![]() ,
and simultaneously
,
and simultaneously
![]() (Lin & Papaloizou 1986). Motion of the satellite is then coupled with
the disc inflow, so that
(Lin & Papaloizou 1986). Motion of the satellite is then coupled with
the disc inflow, so that
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fgr2.eps}\end{figure}](/articles/aa/full/2001/35/aa1036/Timg107.gif)
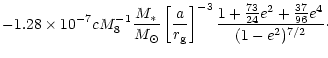
![]() ,
one could explore the relative ratio
of the hydrodynamical versus gravitational radiation losses in other
regimes of the satellite-disc interaction. In this way, the relevant
formulae (those which apply in the course of orbiter evolution) are
,
one could explore the relative ratio
of the hydrodynamical versus gravitational radiation losses in other
regimes of the satellite-disc interaction. In this way, the relevant
formulae (those which apply in the course of orbiter evolution) are
![]() ). For
definiteness, we adopt the disc model (iii) and the condition of
). For
definiteness, we adopt the disc model (iii) and the condition of
![]() when the transition in the disc occurs. We
checked by modifying the value of
when the transition in the disc occurs. We
checked by modifying the value of
![]() by a factor of 10that the qualitative picture of orbital evolution does not depend on
its exact choice and also that numerical results remain similar.
by a factor of 10that the qualitative picture of orbital evolution does not depend on
its exact choice and also that numerical results remain similar.
![]() ,
which we expressed in
terms of the orbital decay
,
which we expressed in
terms of the orbital decay ![]() .
Let us recall that dimensionless
parameter characterizing compactness of the orbiter can be introduced in
different ways. While
.
Let us recall that dimensionless
parameter characterizing compactness of the orbiter can be introduced in
different ways. While
![]() stands directly in
the description of star-disc collisions, the usual factor
stands directly in
the description of star-disc collisions, the usual factor
![]() determines the importance of
general relativity effects near the surface of a compact body:
determines the importance of
general relativity effects near the surface of a compact body:
![]() .
We treat motion in the Newtonian regime
and we only take the possibility of the satellite capture into account
by removing the orbiter from a sample if its trajectory plunges too
close to the central mass, below a marginally stable orbit. Another
dimensionless quantity has also been designated as the compactness
parameter when describing accretion onto compact objects,
.
We treat motion in the Newtonian regime
and we only take the possibility of the satellite capture into account
by removing the orbiter from a sample if its trajectory plunges too
close to the central mass, below a marginally stable orbit. Another
dimensionless quantity has also been designated as the compactness
parameter when describing accretion onto compact objects,
![]() .
It considers the effect of radiation luminosity L acting through a
cross-section
.
It considers the effect of radiation luminosity L acting through a
cross-section
![]() in the medium, however, we can safely
ignore radiation pressure on macroscopic satellites hereafter.
in the medium, however, we can safely
ignore radiation pressure on macroscopic satellites hereafter.
![]() (
(![]()
![]() ), and on the fraction of those dragged into the
disc plane in this region. A simple smooth disc can be destroyed,
especially in the process of gap formation (the case of sufficiently
large
), and on the fraction of those dragged into the
disc plane in this region. A simple smooth disc can be destroyed,
especially in the process of gap formation (the case of sufficiently
large ![]() and small h); the models (i) and (v) are particularly
susceptible to the occurence of multiple gaps. Very roughly, if
and small h); the models (i) and (v) are particularly
susceptible to the occurence of multiple gaps. Very roughly, if
![]() of
the total number of N=104 satellites get aligned with the disc at late times
(a result of our computations for the model (iii)), then their Roche lobes
might cover an area of the order
of
the total number of N=104 satellites get aligned with the disc at late times
(a result of our computations for the model (iii)), then their Roche lobes
might cover an area of the order
![]() .
This is just comparable with the total disc surface for
.
This is just comparable with the total disc surface for
![]() ,
however, recall that
there are more conditions for the gap formation depending on the disc
model. Also, effects of two-body relaxation and of satellite scattering
in the gravitational potential of the disc are expected to decrease
the fraction of aligned bodies when these effects are taken into account.
,
however, recall that
there are more conditions for the gap formation depending on the disc
model. Also, effects of two-body relaxation and of satellite scattering
in the gravitational potential of the disc are expected to decrease
the fraction of aligned bodies when these effects are taken into account.