Further constraints can be obtained by studying the effect of the
evolution of the ionising background on the evolution of absorbers.
Davé et al. (1999) have studied the evolution of the low-redshift
Ly![]() forest in a hydrodynamic cosmological simulation, adopting an UV
ionising background with the same redshift evolution as that of
Haardt & Madau (1996). They found a sharp transition at z=1.7 for the
number density evolution,
forest in a hydrodynamic cosmological simulation, adopting an UV
ionising background with the same redshift evolution as that of
Haardt & Madau (1996). They found a sharp transition at z=1.7 for the
number density evolution,
![]() .
The change in evolution is primarily
due to the drop in the UV ionising background, resulting from the decline in
the QSO population. The formation of structure by gravitational growth
plays only a minor role in the evolution. In the absence of structure
evolution, it is possible to derive an analytical approximation for
the evolution of
.
The change in evolution is primarily
due to the drop in the UV ionising background, resulting from the decline in
the QSO population. The formation of structure by gravitational growth
plays only a minor role in the evolution. In the absence of structure
evolution, it is possible to derive an analytical approximation for
the evolution of
![]() with
with ![]() and the Hubble expansion. For
clouds in photo-ionisation equilibrium with the background, it is
easy to show that the evolution of lines above a given threshold in column
density can be written as (Davé et al. 1999)
and the Hubble expansion. For
clouds in photo-ionisation equilibrium with the background, it is
easy to show that the evolution of lines above a given threshold in column
density can be written as (Davé et al. 1999)
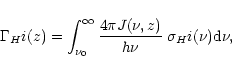 |
(13) |
In Fig. 4 we show
![]() for Lyman forest clouds in the column
density range
for Lyman forest clouds in the column
density range
![]() .
Data points
come from several sources in the literature and from new high resolution
VLT/UVES spectra of three QSO (Kim et al. 2001). For each of our models,
we have computed
.
Data points
come from several sources in the literature and from new high resolution
VLT/UVES spectra of three QSO (Kim et al. 2001). For each of our models,
we have computed
![]() and we have derived the evolution of
and we have derived the evolution of
![]() according to Eq. (12), for the two cosmologies adopted
in this paper. The evolution has been normalized to the observed values
for 2<z<3. In this redshift range, the UV background is nearly flat for
any of the models and it is easy to show, from Eq. (12), that
according to Eq. (12), for the two cosmologies adopted
in this paper. The evolution has been normalized to the observed values
for 2<z<3. In this redshift range, the UV background is nearly flat for
any of the models and it is easy to show, from Eq. (12), that
![]() ,
independently of the cosmology.
By fitting the observed data, Kim et al. (2001) have derived
,
independently of the cosmology.
By fitting the observed data, Kim et al. (2001) have derived
![]() for z>1.5. A value
for z>1.5. A value
![]() can well
reproduce the evolution derived from the observations. This is consistent
with fits of the density distribution, that give
can well
reproduce the evolution derived from the observations. This is consistent
with fits of the density distribution, that give
![]() over
over
![]() at
at ![]() (Kim et al. 2001). On the other hand, weaker lines (
(Kim et al. 2001). On the other hand, weaker lines (
![]() )
are known to have a flatter
distribution in column density (
)
are known to have a flatter
distribution in column density (
![]() ;
Giallongo et al. 1996; Kim et al. 2001). This will produce a slower redshift
evolution, as observed in this column density range for z>1.5(
;
Giallongo et al. 1996; Kim et al. 2001). This will produce a slower redshift
evolution, as observed in this column density range for z>1.5(
![]() ;
Kim et al. 2001).
We remind here that in Sect. 2.1 we have used
;
Kim et al. 2001).
We remind here that in Sect. 2.1 we have used
![]() ,
that
provides a good description of the density distribution over a much
larger column density range.
,
that
provides a good description of the density distribution over a much
larger column density range.
The analysis of Kim et al. (2001) shows that the change in evolution
occurs at
![]() ,
rather than at
,
rather than at
![]() ,
as previously
suggested (Weymann et al. 1998). In Fig. 4 the break at
,
as previously
suggested (Weymann et al. 1998). In Fig. 4 the break at
![]() can be reproduced if the contribution of galaxies
to the background is dominant. This is because of the rapid decrease
of the star-formation rate (and of
can be reproduced if the contribution of galaxies
to the background is dominant. This is because of the rapid decrease
of the star-formation rate (and of
![]() )
below this
redshift (Fig. 2). The photo-ionisation rate of a pure QSOs
background, instead, peaks at
)
below this
redshift (Fig. 2). The photo-ionisation rate of a pure QSOs
background, instead, peaks at ![]() and has a slower evolution
with z. It is interesting to note that the modelled evolution is
closer to the observed data for the
and has a slower evolution
with z. It is interesting to note that the modelled evolution is
closer to the observed data for the ![]() -cosmology. For the
Einstein-De Sitter universe,
-cosmology. For the
Einstein-De Sitter universe,
![]() grows for z<1, which is not
observed. However, the discrepancy may be mitigated when the effect of the
formation of structures on
grows for z<1, which is not
observed. However, the discrepancy may be mitigated when the effect of the
formation of structures on
![]() is taken into account (Davé et al. 1999).
is taken into account (Davé et al. 1999).
The modelled
![]() do not depend on our approximation of a purely
absorbing intergalactic medium, since the contribution of cloud emission
to
do not depend on our approximation of a purely
absorbing intergalactic medium, since the contribution of cloud emission
to
![]() is nearly constant with redshift
(see Fig. 6 in Haardt & Madau 1996).
is nearly constant with redshift
(see Fig. 6 in Haardt & Madau 1996).
Copyright ESO 2001