The mean specific intensity of the Ultraviolet background
![]() ,
as seen at a frequency
,
as seen at a frequency
![]() by an observer at redshift
by an observer at redshift
![]() ,
can be
derived from
,
can be
derived from
The emissivity
![]() should include a contribution both from
direct sources of UV radiation (e.g. QSOs and galaxies) and from the IGM
clouds themselves, through continuum radiative recombination of the gas
(Haardt & Madau 1996). For the sake of simplicity, we consider here the
case of a purely absorbing IGM, thus omitting radiative recombination.
The effect of this omission will be discussed later.
should include a contribution both from
direct sources of UV radiation (e.g. QSOs and galaxies) and from the IGM
clouds themselves, through continuum radiative recombination of the gas
(Haardt & Madau 1996). For the sake of simplicity, we consider here the
case of a purely absorbing IGM, thus omitting radiative recombination.
The effect of this omission will be discussed later.
The line element can be written as
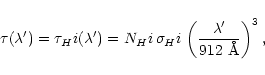 |
(4) |
The ionisation of He I at 504 Å is not considered: He I
being almost completely ionised, its contribution to the total opacity is
negligible (Haard & Madau 1996). For completeness, we have included the
contribution of He II ionisation to the opacity, although it
does not affect the results presented in this paper.
He II is ionised for
![]() Å: thus,
Å: thus,
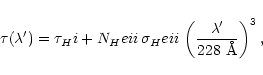 |
(5) |
For the redshift and column density distribution of absorption lines we
have adopted the usual form
| A |
|
|||
| 0.50 | 1.46 | 0.16 |
|
|
| 0.13 | 1.46 | 2.19 |
|
z> 1 |
| 0.17 | 1.46 | 1.55 |
|
As already pointed out by many authors
(Madau 1991, 1992; Haardt & Madau 1996),
the UV background becomes more dominated by local sources as the redshift
increases. This can be seen in Fig. 1, where we show the
distance in redshift
![]() corresponding to an
effective optical depth
corresponding to an
effective optical depth
![]() ,
as a
function of
,
as a
function of
![]() .
For radiation at
.
For radiation at
![]() Å
Å ![]() decreases from 1.8 at
decreases from 1.8 at
![]() to 0.08 at
to 0.08 at
![]() .
The same trend can be
seen for
.
The same trend can be
seen for
![]() Å but with larger values of
Å but with larger values of
![]() (less absorption), because of the
dependence of the H I ionisation cross-section on the wavelength.
Since only radiation from local sources can easily reach
(less absorption), because of the
dependence of the H I ionisation cross-section on the wavelength.
Since only radiation from local sources can easily reach
![]() ,
it is not necessary to compute the integral in
Eq. (1) up to
,
it is not necessary to compute the integral in
Eq. (1) up to ![]() (or to the maximum z for which
UV emitting sources are available). We have used in our calculation
(or to the maximum z for which
UV emitting sources are available). We have used in our calculation
![]() .
.
The absorber distribution we have adopted produces opacities that are very
similar to those of Haardt & Madau (1996). Fardal et al. (1998,
see also Shull et al. 1999) have derived
values for A, ![]() and
and ![]() by fitting the distribution of
absorption lines in several ranges of column density. The opacity provided
by their model is smaller than the one presented here. For example, at
by fitting the distribution of
absorption lines in several ranges of column density. The opacity provided
by their model is smaller than the one presented here. For example, at
![]() we reach
we reach
![]() for
for
![]() ,
while it is
,
while it is
![]() for model A2 in Fardal et al. (1998).
For the same emissivities, the opacity of Fardal et al. (1998) will
result in a UV background higher than ours. The difference increases
with
for model A2 in Fardal et al. (1998).
For the same emissivities, the opacity of Fardal et al. (1998) will
result in a UV background higher than ours. The difference increases
with
![]() and reaches 0.1 dex at
and reaches 0.1 dex at
![]() .
.
Boyle et al. (2000) provide the best-fitting parameters of the
B-band luminosity function for the two cosmologies adopted in this
paper. The B-band proper emissivity can then be derived through the
integral
Boyle et al. (2000) derived the B-band luminosity function from
observations in the QSOs UV restframe, applying the K-correction
for the composite QSO spectrum of Cristiani & Vio (1990). For
consistency, we have used the same spectrum to derive the UV emissivity
for
![]() Å. For
Å. For
![]() Å we have used a power-law,
Å we have used a power-law,
![]() ,
as measured on a sample of
radio-quiet QSOs observed with HST (Zheng et al. 1997).
,
as measured on a sample of
radio-quiet QSOs observed with HST (Zheng et al. 1997).
We have also derived the QSO emissivity from the work of
La Franca & Cristiani (1997). They fitted the luminosity function on a
sample of 326 objects (the Homogeneous Bright QSO Survey) by using a
different luminosity evolution. Results obtained with this emissivity
are very similar to those for the emissivity discussed above
and are not presented in this paper.
![\begin{figure}
\par\includegraphics[width=12cm]{H2870f2.eps}\end{figure}](/articles/aa/full/2001/34/aah2870/Timg110.gif) |
Figure 2:
Comoving UV emissivity in a flat
|
The galactic emissivity in the ionising UV has been derived following the
method outlined by Madau et al. (1998). The comoving UV emissivity at
![]() Å (rest frame) can be derived from galaxy surveys
as a function of the redshift. Because UV light is mainly produced by
short-lived OB stars, it is possible to convert the UV emissivity into a
star-formation history of the universe. If we assume that the mean
luminosity evolution of the galaxies in the universe can be described with
a single galactic spectrum compatible with the derived star-formation
history, a stellar population synthesis model can be used to derive the
emissivity at any wavelength.
Å (rest frame) can be derived from galaxy surveys
as a function of the redshift. Because UV light is mainly produced by
short-lived OB stars, it is possible to convert the UV emissivity into a
star-formation history of the universe. If we assume that the mean
luminosity evolution of the galaxies in the universe can be described with
a single galactic spectrum compatible with the derived star-formation
history, a stellar population synthesis model can be used to derive the
emissivity at any wavelength.
We have used the latest version of the Bruzual & Charlot (1993) stellar
population synthesis models, updated with a new set of stellar evolutionary
tracks and spectral libraries (Bruzual & Charlot 2001; see also
Liu et al. 2000). A Salpeter (1955) IMF with
![]() has been adopted. We have chosen the quasi-empirical
library of stellar spectra for solar metallicity, derived from observations
for
has been adopted. We have chosen the quasi-empirical
library of stellar spectra for solar metallicity, derived from observations
for
![]() Å and from model of stellar atmospheres for
Å and from model of stellar atmospheres for
![]() Å. The conversion factor between UV luminosity and SFR has
been derived from the adopted stellar model, in the limit of continuous
star-formation (Madau et al. 1998; Kennicutt 1998). For radiation
at
Å. The conversion factor between UV luminosity and SFR has
been derived from the adopted stellar model, in the limit of continuous
star-formation (Madau et al. 1998; Kennicutt 1998). For radiation
at
![]() Å we obtain
Å we obtain
The star-formation history at z<2 has been calibrated on the UV comoving
emissivities tabulated by Madau et al. (1998) for a flat
![]() universe. Emissivities at
universe. Emissivities at
![]() Å have been derived from the Canada-France Redshift
Survey (Lilly et al. 1996) in the range
0.2 < z < 1 and from a HDF-north
sample of objects with optical photometric redshifts for 1<z<2
(Connolly et al. 1997). Madau et al. (1996) have derived the emissivity
at
Å have been derived from the Canada-France Redshift
Survey (Lilly et al. 1996) in the range
0.2 < z < 1 and from a HDF-north
sample of objects with optical photometric redshifts for 1<z<2
(Connolly et al. 1997). Madau et al. (1996) have derived the emissivity
at
![]() Å from objects selected in two redshift ranges at
Å from objects selected in two redshift ranges at
![]() and
and ![]() ,
from object selected on the HDF-north with the UV
dropout technique. The lower emissivities at z> 2 suggested that the star
formation rate has reached a maximum at
,
from object selected on the HDF-north with the UV
dropout technique. The lower emissivities at z> 2 suggested that the star
formation rate has reached a maximum at
![]() .
However, a different
picture emerged from the ground-based survey of Steidel et al. (1999).
They selected Lyman break galaxies on a larger area than the HDF, refining
the colour selection criteria with spectroscopic observations of a few object
in the sample. The derived emissivity (at
.
However, a different
picture emerged from the ground-based survey of Steidel et al. (1999).
They selected Lyman break galaxies on a larger area than the HDF, refining
the colour selection criteria with spectroscopic observations of a few object
in the sample. The derived emissivity (at
![]() Å) for
Å) for ![]() is
still consistent with the Madau et al. (1996) value, while the emissivity
at
is
still consistent with the Madau et al. (1996) value, while the emissivity
at ![]() does not show a steep decline. A value for the emissivity
at
does not show a steep decline. A value for the emissivity
at
![]() Å in the redshift bin
2.5 < z < 3.5 can be derived
from the luminosity function fitted by Poli et al. (2001) on a
combined ground-based and HST database. The datapoints are shown in
Fig. 2 as a function of redshift. We have corrected the emissivities
of Steidel et al. (1999) and Poli et al. (2001) to include all objects with
luminosities from 0 to
Å in the redshift bin
2.5 < z < 3.5 can be derived
from the luminosity function fitted by Poli et al. (2001) on a
combined ground-based and HST database. The datapoints are shown in
Fig. 2 as a function of redshift. We have corrected the emissivities
of Steidel et al. (1999) and Poli et al. (2001) to include all objects with
luminosities from 0 to ![]() .
The large errors in the data derived from
Steidel et al. (1999)
and Poli et al. (2001) reflect the uncertainties in the faint-end slope
.
The large errors in the data derived from
Steidel et al. (1999)
and Poli et al. (2001) reflect the uncertainties in the faint-end slope
![]() of the Schechter (1976) luminosity function.
Steidel et al. (1999) derive
of the Schechter (1976) luminosity function.
Steidel et al. (1999) derive
![]() and Poli et al. (2001)
and Poli et al. (2001)
![]() .
In the Madau et al. (1998) tabulation,
.
In the Madau et al. (1998) tabulation,
![]() was used.
was used.
A smooth star-formation history has been derived from the observed UV emissivities in Fig. 2, by using Eq. (11) and correcting for dust internal extinction according to the Calzetti's (1997) attenuation law. At high redshift, we have adopted the flat star-formation history suggested by the work of Steidel et al. (1999). Synthetic galactic spectra have then been produced with the Bruzual & Charlot (2001) code. In Fig. 2 we show the evolution of the modelled UV emissivity at 1500 Å (solid line) and at 2800 Å (dotted line), for a colour excess E(B-V)=0.1. The model is compatible with both data at 2800 Å and z<2 and data at 1500 Å (and 1700 Å) and z>2. For the chosen E(B-V), the model is also consistent with the evolution of the emissivity in the optical-NIR regime for z<2, as tabulated by Madau et al. (1998, not shown in Fig. 2).
Unfortunately, it has not been possible to repeat the same procedure to
model the emissivity (and star-formation history) in ![]() -cosmology.
Only Poli et al. (2001) present a luminosity function derived assuming
-cosmology.
Only Poli et al. (2001) present a luminosity function derived assuming
![]() .
Steidel et al. (1999) give the
emissivity for the objects visible in their survey, but they do not
provide a luminosity function for an extrapolation to fainter
luminosities. Therefore, we have used the model of the emissivity for
.
Steidel et al. (1999) give the
emissivity for the objects visible in their survey, but they do not
provide a luminosity function for an extrapolation to fainter
luminosities. Therefore, we have used the model of the emissivity for
![]() and scaled it with a redshift-dependent correction:
for sufficiently small redshift bin, it can be shown that the ratio
of the emissivities in the flat
and scaled it with a redshift-dependent correction:
for sufficiently small redshift bin, it can be shown that the ratio
of the emissivities in the flat ![]() - and Einstein-De Sitter
cosmologies is
- and Einstein-De Sitter
cosmologies is
![]() .
The emissivity
derived in this way is consistent with the data of Poli et al. (2001).
Because of Eq. (11), the same ratios applies to the
star-formation histories.
.
The emissivity
derived in this way is consistent with the data of Poli et al. (2001).
Because of Eq. (11), the same ratios applies to the
star-formation histories.
The synthetic spectrum has then been used to derive the emissivity for
the ionising UV. Due to the absence of observations, synthetic spectra
rely on models of stellar atmospheres for
![]() Å.
Charlot & Longhetti (2001) compared stellar spectra from different models
and concluded that discrepancies on the ionising flux are not higher than
0.1 dex. The uncertainty on our modelled emissivity also depends
on the uncertainties in the determination of the SFR. To quantify the
uncertainties in the adopted model, we have computed the effect on the
emissivity of the variation of the basic ingredients of the
Bruzual & Charlot (2001) model (IMF, metallicity, stellar libraries). We
have used the same description for the UV emissivity at 1500 Å as in
the main model (solid line in Fig. 2) and converted it into
a star-formation history by using a conversion factor appropriate for
the selected IMF and stellar spectra. The synthetic spectra obtained
in this way typically differ by less than 0.2 dex at the ionisation
limit and 0.3 dex at 600 Å.
Å.
Charlot & Longhetti (2001) compared stellar spectra from different models
and concluded that discrepancies on the ionising flux are not higher than
0.1 dex. The uncertainty on our modelled emissivity also depends
on the uncertainties in the determination of the SFR. To quantify the
uncertainties in the adopted model, we have computed the effect on the
emissivity of the variation of the basic ingredients of the
Bruzual & Charlot (2001) model (IMF, metallicity, stellar libraries). We
have used the same description for the UV emissivity at 1500 Å as in
the main model (solid line in Fig. 2) and converted it into
a star-formation history by using a conversion factor appropriate for
the selected IMF and stellar spectra. The synthetic spectra obtained
in this way typically differ by less than 0.2 dex at the ionisation
limit and 0.3 dex at 600 Å.
Spectra at
![]() Å also need to be corrected for the
internal absorption by the galaxy interstellar medium.
We describe this correction with the parameter
Å also need to be corrected for the
internal absorption by the galaxy interstellar medium.
We describe this correction with the parameter
![]() ,
i.e.
the fraction of Lyman-continuum photons that can escape into the IGM
without being absorbed by the interstellar medium, either gas or dust.
A wide range of values can be found in the literature for
,
i.e.
the fraction of Lyman-continuum photons that can escape into the IGM
without being absorbed by the interstellar medium, either gas or dust.
A wide range of values can be found in the literature for
![]() ,
derived both from models of radiative transfer and observations of H I
recombination lines
(
,
derived both from models of radiative transfer and observations of H I
recombination lines
(
![]() ;
for a review, see Barkana & Loeb 2001).
UV observations of local starbursts suggest
;
for a review, see Barkana & Loeb 2001).
UV observations of local starbursts suggest
![]() (Leitherer et al. 1995; Hurwitz et al. 1997;
Heckman et al. 2001).
Steidel et al. (2001) analysed a composite spectrum of 29 Lyman-break
galaxies at
(Leitherer et al. 1995; Hurwitz et al. 1997;
Heckman et al. 2001).
Steidel et al. (2001) analysed a composite spectrum of 29 Lyman-break
galaxies at ![]() .
They derived a ratio between the flux
densities at 1500 Å and 900 Å
.
They derived a ratio between the flux
densities at 1500 Å and 900 Å
![]() ,
after
correcting for the differential absorption due to the intervening IGM.
The
f1500/f900 ratio for the unattenuated synthetic spectrum
that we have used is very similar,
,
after
correcting for the differential absorption due to the intervening IGM.
The
f1500/f900 ratio for the unattenuated synthetic spectrum
that we have used is very similar,
![]() .
If we assume that 40% of the radiation at 1500 Å is absorbed by dust
(as obtained from the Calzetti's attenuation law
with
E(B-V)=0.1), the observed
f1500/f900 ratio is equivalent to
.
If we assume that 40% of the radiation at 1500 Å is absorbed by dust
(as obtained from the Calzetti's attenuation law
with
E(B-V)=0.1), the observed
f1500/f900 ratio is equivalent to
![]() (if the internal absorption in the Lyman
continuum do not change significantly with
(if the internal absorption in the Lyman
continuum do not change significantly with ![]() ).
Because of the increase of the disk density with the redshift,
).
Because of the increase of the disk density with the redshift,
![]() is expected to decrease with z; it is also found to
depend heavily on the details of the distribution of the sources and the
gas, i.e. whether the stars and/or gas are clumped or not (Wood & Loeb 2000).
In this work, we will use a wavelength and redshift independent
is expected to decrease with z; it is also found to
depend heavily on the details of the distribution of the sources and the
gas, i.e. whether the stars and/or gas are clumped or not (Wood & Loeb 2000).
In this work, we will use a wavelength and redshift independent
![]() ,
by which we multiply the synthetic spectrum at
,
by which we multiply the synthetic spectrum at
![]() Å. We will show results for
Å. We will show results for
![]() and
0.40, to cover the range of values suggested by local and
and
0.40, to cover the range of values suggested by local and ![]() observations, and for an intermediate value,
observations, and for an intermediate value,
![]() .
.
Finally, the galactic emissivity has been converted from comoving to
proper, multiplying by (1+z)3. The total emissivity in
Eq. (1) is the sum of the QSOs and the galaxy
contribution.
![\begin{figure}
\par\includegraphics[width=12cm]{H2870f3.eps}\end{figure}](/articles/aa/full/2001/34/aah2870/Timg134.gif) |
Figure 3:
UV background at
|
Copyright ESO 2001