

Up: Global physical conditions of galaxies
3 Physical conditions of interstellar medium
Together with the [O I]63  m and 145
m and 145  m lines,
[C II]158
m lines,
[C II]158  m can be used to derive
the physical conditions of the line-emitting regions based on PDR models
(e.g., Tielens & Hollenbach
1985; Wolfire et al. 1990; Hollenbach & Tielens
1997; Kaufman et al. 1999),
in which the major model parameters
are the incident FUV radiation field flux
m can be used to derive
the physical conditions of the line-emitting regions based on PDR models
(e.g., Tielens & Hollenbach
1985; Wolfire et al. 1990; Hollenbach & Tielens
1997; Kaufman et al. 1999),
in which the major model parameters
are the incident FUV radiation field flux  in units of the
solar neighborhood
value (
in units of the
solar neighborhood
value (
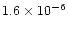 Wm-2, Habing 1968)
and the neutral hydrogen gas density n.
However, the [C II] line could also originate from ionized regions
and the fraction of the contribution cannot be estimated a
priori.
Wm-2, Habing 1968)
and the neutral hydrogen gas density n.
However, the [C II] line could also originate from ionized regions
and the fraction of the contribution cannot be estimated a
priori.
To estimate the contribution to [C II]158  m from PDRs, we take
two approaches similar to Malhotra et al. (2001b).
First we assume that all the emission of [O I]63
m from PDRs, we take
two approaches similar to Malhotra et al. (2001b).
First we assume that all the emission of [O I]63  m and
far-infrared
continuum (
m and
far-infrared
continuum (
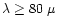 m) comes from PDRs. Since the temperature
of sub-micron sized dust grains is determined by the intensity of the incident
radiation (e.g., Onaka 2000),
m) comes from PDRs. Since the temperature
of sub-micron sized dust grains is determined by the intensity of the incident
radiation (e.g., Onaka 2000),  can be estimated
from the dust temperature
can be estimated
from the dust temperature 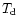 derived by Eq. (1).
We used a semi-analytical equation of
derived by Eq. (1).
We used a semi-analytical equation of  and
and 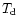 given by
Hollenbach et al. (1991) with
AV = 0.5 because
a major fraction of [C II]158
given by
Hollenbach et al. (1991) with
AV = 0.5 because
a major fraction of [C II]158  m and [O I]63
m and [O I]63  m
emissions stem from the region of
m
emissions stem from the region of
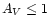 (Kaufman et al. 1999).
For M 82 we derive
(Kaufman et al. 1999).
For M 82 we derive
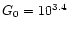 ,
while Kaufman et al.
(1999) estimated
,
while Kaufman et al.
(1999) estimated
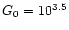 by taking account
of several observed line intensities, suggesting that
the present method provides a reasonable estimate of
by taking account
of several observed line intensities, suggesting that
the present method provides a reasonable estimate of  .
.
Then we compare the ratio of [O I]
 with the PDR model of
Kaufman
et al. (1999) with the derived
with the PDR model of
Kaufman
et al. (1999) with the derived  to estimate n.
Finally we estimate the intensity of [C II]158
to estimate n.
Finally we estimate the intensity of [C II]158  m from PDRs with
the derived
m from PDRs with
the derived  and n.
The current estimate of the flux uncertainty is 20% and there
may be an uncertainty in the PDR model due to the assumed geometry.
While FIR may be underestimated by a few tens %
in the present analysis,
it does not introduce a significant error compared to other uncertainties.
and n.
The current estimate of the flux uncertainty is 20% and there
may be an uncertainty in the PDR model due to the assumed geometry.
While FIR may be underestimated by a few tens %
in the present analysis,
it does not introduce a significant error compared to other uncertainties.
Figure 4 shows  and n against the color
R(60/100).
and n against the color
R(60/100).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2828f4.eps}\end{figure}](/articles/aa/full/2001/32/aah2828/Timg71.gif) |
Figure 4:
a) FUV incident flux estimated by the dust temperature,  ,
and the derived cloud gas density, n, against the far-infrared color
R(60/100).
Filled circles indicate ,
and the derived cloud gas density, n, against the far-infrared color
R(60/100).
Filled circles indicate  and open squares n [cm-3].
b) Ratio of the [C II] intensity from PDRs to the observed total
[C II] intensity vs. the R(60/100).
and open squares n [cm-3].
b) Ratio of the [C II] intensity from PDRs to the observed total
[C II] intensity vs. the R(60/100). |
The error in  comes from the uncertainty in
comes from the uncertainty in
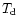 ,
while that in n is estimated from the uncertainty in [O I]
,
while that in n is estimated from the uncertainty in [O I]
 to
be about
to
be about
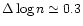 based on the PDR models.
Both parameters,
based on the PDR models.
Both parameters,  and n, increase clearly with
R(60/100) and n is found to be almost
proportional to
and n, increase clearly with
R(60/100) and n is found to be almost
proportional to  (
(
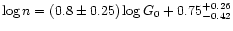 ,
see also Fig. 10).
The trend mainly comes from the observed constancy of [O I]
,
see also Fig. 10).
The trend mainly comes from the observed constancy of [O I]
 against the color.
In the PDR model the photoelectric heating efficiency is roughly a function
of
against the color.
In the PDR model the photoelectric heating efficiency is roughly a function
of
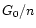 (Bakes & Tielens 1994).
For
(Bakes & Tielens 1994).
For
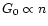 ,
the heating efficiency does not change and
thus [O I]
,
the heating efficiency does not change and
thus [O I]
 stays constant.
The [C II]158
stays constant.
The [C II]158  m
m
 ,
on the other hand, decreases
because the collisional de-excitation becomes efficient as n increases:
the [C II] line has a lower critical density for excitation
(
,
on the other hand, decreases
because the collisional de-excitation becomes efficient as n increases:
the [C II] line has a lower critical density for excitation
(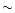
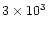 cm-3)
than [O I]63
cm-3)
than [O I]63  m (
m (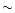
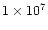 cm-3).
In this situation, we expect an increase in the gas temperature.
Because the gas temperature is already sufficiently high in the parameter
range in question, the increase in the temperature does not affect
the line intensities appreciably.
Hence the decrease in [C II]
cm-3).
In this situation, we expect an increase in the gas temperature.
Because the gas temperature is already sufficiently high in the parameter
range in question, the increase in the temperature does not affect
the line intensities appreciably.
Hence the decrease in [C II]
 with color can be attributed
to the increase in the collisional de-excitation of the [C II]
transition for the present sample of the galaxies.
The [C II]158
with color can be attributed
to the increase in the collisional de-excitation of the [C II]
transition for the present sample of the galaxies.
The [C II]158  m emission from PDRs is estimated to be
m emission from PDRs is estimated to be 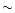
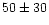 % of the total observed
[C II]158
% of the total observed
[C II]158  m emission in the present analysis and the
fraction of the PDR component is indicated to decrease with R(60/100)(Fig. 4b). Therefore, the decrease in the total
[C II]/FIR is attributed to the decrease in the PDR component due to the
thermalization of the [C II] transition.
m emission in the present analysis and the
fraction of the PDR component is indicated to decrease with R(60/100)(Fig. 4b). Therefore, the decrease in the total
[C II]/FIR is attributed to the decrease in the PDR component due to the
thermalization of the [C II] transition.
In order to examine the reliability of the present data reduction and
analysis we can compare the present results
with those of previous works for some individual galaxies.
The comparison is summarized in Table 4.
Colbert et al. (1999) and Unger et al. (2000) analyzed the same
LWS data and derived  and n by
using the PDR models of Kaufman et al. (1999) for M 82 and Cen A,
respectively.
The present analysis provides fairly good agreement with their results.
The line intensities derived in the present study also agree with those by
Braine & Hughes (1999) within the measurement errors.
Carral et al. (1994) reported the results of observations of NGC 253
and NGC 3256 by the KAO
and obtained
and n by
using the PDR models of Kaufman et al. (1999) for M 82 and Cen A,
respectively.
The present analysis provides fairly good agreement with their results.
The line intensities derived in the present study also agree with those by
Braine & Hughes (1999) within the measurement errors.
Carral et al. (1994) reported the results of observations of NGC 253
and NGC 3256 by the KAO
and obtained  and n based on the PDR models of
Wolfire et al. (1990). While the line fluxes are in agreement
with the present results
within the errors except for [O III]88
and n based on the PDR models of
Wolfire et al. (1990). While the line fluxes are in agreement
with the present results
within the errors except for [O III]88  m of NGC 253, the present
results indicate systematically low densities. The difference can be
attributed to the relatively
high gas temperature with the same
m of NGC 253, the present
results indicate systematically low densities. The difference can be
attributed to the relatively
high gas temperature with the same  and n in the models of
Kaufman et al. because their models include the additional gas heating due to
polycyclic aromatic hydrocarbons (PAHs).
The [C II] emission other than the PDR origin may be ascribed to the
extended low density warm ionized medium (ELDWIM). A large fraction of
[N II]122
and n in the models of
Kaufman et al. because their models include the additional gas heating due to
polycyclic aromatic hydrocarbons (PAHs).
The [C II] emission other than the PDR origin may be ascribed to the
extended low density warm ionized medium (ELDWIM). A large fraction of
[N II]122  m line emission is thought to stem mostly from the
ELDWIM (Wright et al. 1991; Heiles 1994; Bennett et al. 1994; Petuchowski et al. 1994).
Figure 5 plots the ratio of the observed [N II]122
m line emission is thought to stem mostly from the
ELDWIM (Wright et al. 1991; Heiles 1994; Bennett et al. 1994; Petuchowski et al. 1994).
Figure 5 plots the ratio of the observed [N II]122  m
intensity to the non-PDR component of [C II]158
m
intensity to the non-PDR component of [C II]158  m.
m.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2828f5.eps}\end{figure}](/articles/aa/full/2001/32/aah2828/Timg79.gif) |
Figure 5:
Ratio of [N II]122  m intensity to the non-PDR
component of [C II]158 m intensity to the non-PDR
component of [C II]158  m against R(60/100). m against R(60/100).
|
The ratio shows a large scatter with a weak trend that the ratio
decreases with R(60/100). Because of the uncertainties the trend may be
spurious (see below).
All the data points are located within the range 0.1-0.7 in
Fig. 5. The line ratio of
[N II]/[C II] in the ionized gas depends on the electron
density, but is insensitive to the temperature of the ionized gas. To estimate
the line ratio expected from ionized gas
we assume
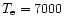 K and the abundance of [ C+]/[H+] =
K and the abundance of [ C+]/[H+] =
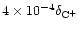 and [ N+]/[H
and [ N+]/[H
![$^+] = 1 \times 10^{-4}
\delta_{{\rm N}^+}$](/articles/aa/full/2001/32/aah2828/img82.gif) with the depletion
factors as
with the depletion
factors as
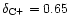 and
and
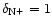 in the following discussion
(Heiles 1994). We adopted the collision coefficients for
N+ from
Stafford et al. (1994) and those for C+ from Heiles
(1994).
Recent HST observations indicate that the interstellar abundance of
carbon and nitrogen in
the gas phase is fairly constant on various lines of sight in our Galaxy as
in the following discussion
(Heiles 1994). We adopted the collision coefficients for
N+ from
Stafford et al. (1994) and those for C+ from Heiles
(1994).
Recent HST observations indicate that the interstellar abundance of
carbon and nitrogen in
the gas phase is fairly constant on various lines of sight in our Galaxy as
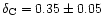 (Sofia et al. 1997) and
(Sofia et al. 1997) and
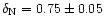 (Meyer et al.
1997). Based on these values the relative abundance of N to C
will increase by 30%.
The following discussion thus has an uncertainty of this level
associated with the assumed abundance.
(Meyer et al.
1997). Based on these values the relative abundance of N to C
will increase by 30%.
The following discussion thus has an uncertainty of this level
associated with the assumed abundance.
The lower boundary of the observed ratio 0.1 is then found to correspond to
the low-density limit of the ratio
in the ionized gas. The upper boundary 0.7 is obtained for a gas with
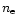 = 120 cm-3.
Petuchowski et al. (1994) reported a large
[N II]122
= 120 cm-3.
Petuchowski et al. (1994) reported a large
[N II]122  m
to 205
m
to 205  m line ratio in the central 850 pc of M 82 compared to the
average ratio of the Milky Way (Wright et al. 1991),
indicating that a fair fraction of the [N II] line emission
comes from the ionized gas of
m line ratio in the central 850 pc of M 82 compared to the
average ratio of the Milky Way (Wright et al. 1991),
indicating that a fair fraction of the [N II] line emission
comes from the ionized gas of
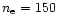 -180 cm-3 in M 82.
The ratio of [N II]122
-180 cm-3 in M 82.
The ratio of [N II]122  m to [C II]158
m to [C II]158  m of non-PDR
origin for M 82
is about 0.3 in the present analysis, suggesting that there may be a
significant contribution to the [CII] emission from
the low density diffuse ionized gas in the outer part (>850 pc) of the
galaxy. The observed intensity
is compatible with the interpretation that
the non-PDR component of [C II]158
m of non-PDR
origin for M 82
is about 0.3 in the present analysis, suggesting that there may be a
significant contribution to the [CII] emission from
the low density diffuse ionized gas in the outer part (>850 pc) of the
galaxy. The observed intensity
is compatible with the interpretation that
the non-PDR component of [C II]158  m comes from the
ionized gas that emits [N II]122
m comes from the
ionized gas that emits [N II]122  m.
m.
The ionized gas also emits a radio continuum. The intensity of free-free
transition is written for
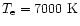 by
by
![\begin{displaymath}I(4.85~\hbox{GHz})\left[\hbox{mJy sr}^{-1}\right] = 3.12 \times 10^{-14}~ n_{\rm e}^2
l,
\end{displaymath}](/articles/aa/full/2001/32/aah2828/img89.gif) |
(3) |
where 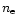 is the electron density in cm-3 and l is the
path
length in cm (Spitzer 1978). The intensity of the
[C II] line from the ionized gas
is given by
is the electron density in cm-3 and l is the
path
length in cm (Spitzer 1978). The intensity of the
[C II] line from the ionized gas
is given by
![\begin{displaymath}I_{\hbox{[C{\sc ii}]}} ({\rm ELDWIM}) = (1/4\pi)
L(T_{\rm e})n(C^+)n_{\rm e} l,
\end{displaymath}](/articles/aa/full/2001/32/aah2828/img90.gif) |
(4) |
where
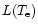 is the cooling function of [C II]158
is the cooling function of [C II]158  m
(e.g., Hayes & Nussbaumer 1984).
For a given [C II]158
m
(e.g., Hayes & Nussbaumer 1984).
For a given [C II]158  m intensity, the corresponding radio
continuum intensity increases with
m intensity, the corresponding radio
continuum intensity increases with 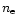 as can
be estimated through Eqs. (3) and (4).
As a conservative upper limit we assume that the non-PDR component of
[C II]
158
as can
be estimated through Eqs. (3) and (4).
As a conservative upper limit we assume that the non-PDR component of
[C II]
158  m emission comes from the ionized gas of density 200 cm-3.
Figure 6 shows the comparison between the predicted and observed
flux densities.
m emission comes from the ionized gas of density 200 cm-3.
Figure 6 shows the comparison between the predicted and observed
flux densities.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2828f6.eps}\end{figure}](/articles/aa/full/2001/32/aah2828/Timg92.gif) |
Figure 6:
The observed 4.85 GHz radio continuum flux density plotted against
the 4.85 GHz radio continuum flux density predicted
from the non-PDR component of [C II]158  m emission (see
text).
The observed radio flux densities are taken from Gregory et al.
(1991, 1994), Becker et al. (1991), and Griffith et al. (1994). m emission (see
text).
The observed radio flux densities are taken from Gregory et al.
(1991, 1994), Becker et al. (1991), and Griffith et al. (1994).
|
We take the 4.85 GHz radio continuum data from Becker et al. (1991),
Gregory & Condon (1991), Gregory et al. (1994), and
Griffith et al. (1994). The beam size of the radio observations
was about
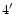 (FWHM).
Observations of 1.49 GHz and 1.425 GHz indicate that most of the radio
continuum
emission comes from the area within about
(FWHM).
Observations of 1.49 GHz and 1.425 GHz indicate that most of the radio
continuum
emission comes from the area within about
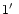 of the center of the
infrared
emission (Condon et al. 1990, 1996). We assume
that the observed 4.85 GHz emission also comes from the region within
the LWS beam. The predicted value shows a positive correlation with the
observed flux density except for Cen A. Cen A is a very strong radio source
and most of the radio emission from Cen A is nonthermal
(e.g. Sreekumar et al. 1999).
The observed radio intensities are larger than the upper limits predicted from
[C II]158
of the center of the
infrared
emission (Condon et al. 1990, 1996). We assume
that the observed 4.85 GHz emission also comes from the region within
the LWS beam. The predicted value shows a positive correlation with the
observed flux density except for Cen A. Cen A is a very strong radio source
and most of the radio emission from Cen A is nonthermal
(e.g. Sreekumar et al. 1999).
The observed radio intensities are larger than the upper limits predicted from
[C II]158  m emission of the non-PDR origin for most of the sample
galaxies. Thus the non-PDR component of
[C II]158
m emission of the non-PDR origin for most of the sample
galaxies. Thus the non-PDR component of
[C II]158  m emission is compatible with the observed
radio continuum intensity
when it arises mostly from the low-density ionized gas for the present
sample of galaxies.
m emission is compatible with the observed
radio continuum intensity
when it arises mostly from the low-density ionized gas for the present
sample of galaxies.
Figure 7 shows the ratio of [O I]145  m to
[O I]63
m to
[O I]63  m against
R(60/100).
m against
R(60/100).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2828f7.eps}\end{figure}](/articles/aa/full/2001/32/aah2828/Timg94.gif) |
Figure 7:
Ratio of the intensity of the [O I]145  m line to the
[O I]63 m line to the
[O I]63  m line against R(60/100). m line against R(60/100). |
The observed ratio is in the range 0.05-0.1 for most galaxies, which is in agreement with the prediction of the
PDR model with the range
of  and n estimated in the present analysis.
The ratio does not exceed 0.1 within a reasonable range of the density and
temperature (Watson 1984).
However, a few galaxies clearly show higher ratios than the model.
They are NGC 4945 and NGC 253, both of which have large inclination angles
(for NGC 4945 and NGC 253,
and n estimated in the present analysis.
The ratio does not exceed 0.1 within a reasonable range of the density and
temperature (Watson 1984).
However, a few galaxies clearly show higher ratios than the model.
They are NGC 4945 and NGC 253, both of which have large inclination angles
(for NGC 4945 and NGC 253,
 and
and
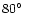 ,
respectively). NGC 520, which shows the third largest ratio, has
,
respectively). NGC 520, which shows the third largest ratio, has
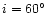 .
The absorption of [O I]63
.
The absorption of [O I]63  m in the interstellar
medium may affect the ratio in these galaxies. For a majority of the
galaxies, however, this effect is probably not significant.
m in the interstellar
medium may affect the ratio in these galaxies. For a majority of the
galaxies, however, this effect is probably not significant.
In the analysis described above it is difficult to properly
evaluate the uncertainties in the comparison with the model.
In order to examine how robust the derived conclusions are,
we take another approach to estimate the PDR contribution to the
[C II]158  m line emission.
Figure 5 indicates that there seems no strong trend in the ratio
of [N II]122
m line emission.
Figure 5 indicates that there seems no strong trend in the ratio
of [N II]122  m to the non-PDR origin of
[C II]158
m to the non-PDR origin of
[C II]158  m.
We thus simply assume that the contribution from the ionized gas to
[C II]158
m.
We thus simply assume that the contribution from the ionized gas to
[C II]158  m
emission is proportional to the [N II]122
m
emission is proportional to the [N II]122  m intensity.
We take a mean value of Fig. 5 as
m intensity.
We take a mean value of Fig. 5 as
![\begin{displaymath}[C{\sc ii}]158~\mu{\rm m}({\rm ELDWIM}) = 3.5 \times
[N{\sc ii}]122~\mu{\rm m}.
\end{displaymath}](/articles/aa/full/2001/32/aah2828/img98.gif) |
(5) |
This relation corresponds to a gas of
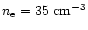 for
for
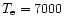 K.
We estimate the intensity of [C II]158
K.
We estimate the intensity of [C II]158  m from the ionized gas
based on the [N II]122
m from the ionized gas
based on the [N II]122  m intensity by
using Eq. (5) and attribute the rest to that coming from
PDRs. We then
estimate
m intensity by
using Eq. (5) and attribute the rest to that coming from
PDRs. We then
estimate  and n from [O I]/[C II] and
([C II]+[O I])
and n from [O I]/[C II] and
([C II]+[O I])
 .
Figure 8a shows
.
Figure 8a shows  and n estimated in this method.
and n estimated in this method.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2828f8.eps}\end{figure}](/articles/aa/full/2001/32/aah2828/Timg100.gif) |
Figure 8:
The results of the analysis based on the assumption
that the contribution from the ionized gas to
[C II]158  m is proportional to [N II]122 m is proportional to [N II]122  m
as given by Eq. (5) (see text).
a) FUV incident flux, m
as given by Eq. (5) (see text).
a) FUV incident flux,  (filled circle) and the gas density,
n (open square) derived from [O I]/[C II] and
([C II]+[O I])
(filled circle) and the gas density,
n (open square) derived from [O I]/[C II] and
([C II]+[O I])
 of the PDR model by Kaufman et al. (1999)
against R(60/100). b) The ratio of the estimated
[C II] intensity from PDRs to the observed total
[C II] intensity against R(60/100).
of the PDR model by Kaufman et al. (1999)
against R(60/100). b) The ratio of the estimated
[C II] intensity from PDRs to the observed total
[C II] intensity against R(60/100). |
The values of  derived in this method are in agreement with
those obtained
in the first approach within the estimated errors. Thus the parameters
derived in
the second method are still compatible with the continuum spectrum of the
LWS spectra. We have obtained the same trend as in the first approach:
both n and
derived in this method are in agreement with
those obtained
in the first approach within the estimated errors. Thus the parameters
derived in
the second method are still compatible with the continuum spectrum of the
LWS spectra. We have obtained the same trend as in the first approach:
both n and  increase with the color and n is roughly
proportional to
increase with the color and n is roughly
proportional to  (see also Fig. 10).
We conclude that the linear increase of n with
(see also Fig. 10).
We conclude that the linear increase of n with
 is a rather secure result for the present sample galaxies.
The weak trend seen in Fig. 5 is not necessarily real.
Figure 8b shows the fraction of the PDR component of
[C II] emission
derived in this analysis, suggesting that the PDR component does not vary
with R(60/100) in contrast to Fig. 4b. Thus
in this analysis the decrease in [C II]
is a rather secure result for the present sample galaxies.
The weak trend seen in Fig. 5 is not necessarily real.
Figure 8b shows the fraction of the PDR component of
[C II] emission
derived in this analysis, suggesting that the PDR component does not vary
with R(60/100) in contrast to Fig. 4b. Thus
in this analysis the decrease in [C II]
 can be
interpreted in terms mainly of the decrease in the ionized component
relative to FIR
as indicated in the decrease in [N II]
can be
interpreted in terms mainly of the decrease in the ionized component
relative to FIR
as indicated in the decrease in [N II]
 (Fig. 2a),
though the decrease in [C II](PDR)
(Fig. 2a),
though the decrease in [C II](PDR)
 due to the
thermalization also contributes partly.
due to the
thermalization also contributes partly.
The ratio of [C II]158  m to 12CO (J=1-0) line
intensity is another measure for the diagnosis of PDRs.
m to 12CO (J=1-0) line
intensity is another measure for the diagnosis of PDRs.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2828f9.eps}\end{figure}](/articles/aa/full/2001/32/aah2828/Timg101.gif) |
Figure 9:
Ratio of the [C II]158  m intensity to the CO (J=1-0) intensity
against R(60/100). The CO emission has not been detected for NGC 6824 and a
lower limit for the ratio is plotted. m intensity to the CO (J=1-0) intensity
against R(60/100). The CO emission has not been detected for NGC 6824 and a
lower limit for the ratio is plotted. |
Because C+ is converted to CO as the gas shielding to prevent
CO from
dissociation becomes efficient, the thickness of C+ layer is a
function of
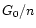 (Mochizuki & Onaka 2001).
The intensity ratio increases with
(Mochizuki & Onaka 2001).
The intensity ratio increases with  and decreases with nand it is a function of
and decreases with nand it is a function of
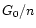 in the range of
in the range of  and n in question (Pierini et al.
1999; Kaufman et al.
1999; Mochizuki & Nakagawa 2000).
Metallicity also plays an important role in the C+ to CO
conversion (Mochizuki et al. 1994). Hence,
unless there is an appreciable variation in the metallicity in the sample
galaxies, the ratio of
[C II]/CO approximately varies with
and n in question (Pierini et al.
1999; Kaufman et al.
1999; Mochizuki & Nakagawa 2000).
Metallicity also plays an important role in the C+ to CO
conversion (Mochizuki et al. 1994). Hence,
unless there is an appreciable variation in the metallicity in the sample
galaxies, the ratio of
[C II]/CO approximately varies with
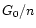 .
Figure 9 plots the ratio against the color.
The CO data are taken from Young et al. (1995), Elfhag et al.
(1996), Aalto et al. (1995), Curran et al. (2001),
Stacey et al. (1991), and Eckart et al. (1990). The CO
observations had the beam size of 45-56
.
Figure 9 plots the ratio against the color.
The CO data are taken from Young et al. (1995), Elfhag et al.
(1996), Aalto et al. (1995), Curran et al. (2001),
Stacey et al. (1991), and Eckart et al. (1990). The CO
observations had the beam size of 45-56
 .
We assume that the CO emission comes mostly from the central part of the
galaxies and did not make any corrections for the beam size.
Except for NGC 6824, the ratio stays almost constant, supporting
.
We assume that the CO emission comes mostly from the central part of the
galaxies and did not make any corrections for the beam size.
Except for NGC 6824, the ratio stays almost constant, supporting
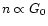 .
The constancy of
.
The constancy of
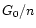 is also
confirmed by the [C II]/CO ratio.
The CO (J=1-0) emission in NGC 6824 was not detected (Young et al.
1995). With the upper limit
the ratio of [C II]/CO is estimated to be larger than 104, which
is in a similar range
to those found in quiet spirals (Smith & Madden 1997).
The values of the observed ratio of the other galaxies
is also
confirmed by the [C II]/CO ratio.
The CO (J=1-0) emission in NGC 6824 was not detected (Young et al.
1995). With the upper limit
the ratio of [C II]/CO is estimated to be larger than 104, which
is in a similar range
to those found in quiet spirals (Smith & Madden 1997).
The values of the observed ratio of the other galaxies
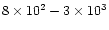 are in agreement with
those observed in Galactic PDRs (Stacey et al. 1991).
It is slightly smaller than the values predicted in the PDR model.
are in agreement with
those observed in Galactic PDRs (Stacey et al. 1991).
It is slightly smaller than the values predicted in the PDR model.


Up: Global physical conditions of galaxies
Copyright ESO 2001
![]() m and 145
m and 145 ![]() m lines,
[C II]158
m lines,
[C II]158 ![]() m can be used to derive
the physical conditions of the line-emitting regions based on PDR models
(e.g., Tielens & Hollenbach
1985; Wolfire et al. 1990; Hollenbach & Tielens
1997; Kaufman et al. 1999),
in which the major model parameters
are the incident FUV radiation field flux
m can be used to derive
the physical conditions of the line-emitting regions based on PDR models
(e.g., Tielens & Hollenbach
1985; Wolfire et al. 1990; Hollenbach & Tielens
1997; Kaufman et al. 1999),
in which the major model parameters
are the incident FUV radiation field flux ![]() in units of the
solar neighborhood
value (
in units of the
solar neighborhood
value (
![]() Wm-2, Habing 1968)
and the neutral hydrogen gas density n.
However, the [C II] line could also originate from ionized regions
and the fraction of the contribution cannot be estimated a
priori.
Wm-2, Habing 1968)
and the neutral hydrogen gas density n.
However, the [C II] line could also originate from ionized regions
and the fraction of the contribution cannot be estimated a
priori.
![]() m from PDRs, we take
two approaches similar to Malhotra et al. (2001b).
First we assume that all the emission of [O I]63
m from PDRs, we take
two approaches similar to Malhotra et al. (2001b).
First we assume that all the emission of [O I]63 ![]() m and
far-infrared
continuum (
m and
far-infrared
continuum (
![]() m) comes from PDRs. Since the temperature
of sub-micron sized dust grains is determined by the intensity of the incident
radiation (e.g., Onaka 2000),
m) comes from PDRs. Since the temperature
of sub-micron sized dust grains is determined by the intensity of the incident
radiation (e.g., Onaka 2000), ![]() can be estimated
from the dust temperature
can be estimated
from the dust temperature ![]() derived by Eq. (1).
We used a semi-analytical equation of
derived by Eq. (1).
We used a semi-analytical equation of ![]() and
and ![]() given by
Hollenbach et al. (1991) with
AV = 0.5 because
a major fraction of [C II]158
given by
Hollenbach et al. (1991) with
AV = 0.5 because
a major fraction of [C II]158 ![]() m and [O I]63
m and [O I]63 ![]() m
emissions stem from the region of
m
emissions stem from the region of
![]() (Kaufman et al. 1999).
For M 82 we derive
(Kaufman et al. 1999).
For M 82 we derive
![]() ,
while Kaufman et al.
(1999) estimated
,
while Kaufman et al.
(1999) estimated
![]() by taking account
of several observed line intensities, suggesting that
the present method provides a reasonable estimate of
by taking account
of several observed line intensities, suggesting that
the present method provides a reasonable estimate of ![]() .
.
![]() with the PDR model of
Kaufman
et al. (1999) with the derived
with the PDR model of
Kaufman
et al. (1999) with the derived ![]() to estimate n.
Finally we estimate the intensity of [C II]158
to estimate n.
Finally we estimate the intensity of [C II]158 ![]() m from PDRs with
the derived
m from PDRs with
the derived ![]() and n.
The current estimate of the flux uncertainty is 20% and there
may be an uncertainty in the PDR model due to the assumed geometry.
While FIR may be underestimated by a few tens %
in the present analysis,
it does not introduce a significant error compared to other uncertainties.
and n.
The current estimate of the flux uncertainty is 20% and there
may be an uncertainty in the PDR model due to the assumed geometry.
While FIR may be underestimated by a few tens %
in the present analysis,
it does not introduce a significant error compared to other uncertainties.
![]() and n against the color
R(60/100).
and n against the color
R(60/100).
![]() K and the abundance of [ C+]/[H+] =
K and the abundance of [ C+]/[H+] =
![]() and [ N+]/[H
and [ N+]/[H
![]() with the depletion
factors as
with the depletion
factors as
![]() and
and
![]() in the following discussion
(Heiles 1994). We adopted the collision coefficients for
N+ from
Stafford et al. (1994) and those for C+ from Heiles
(1994).
Recent HST observations indicate that the interstellar abundance of
carbon and nitrogen in
the gas phase is fairly constant on various lines of sight in our Galaxy as
in the following discussion
(Heiles 1994). We adopted the collision coefficients for
N+ from
Stafford et al. (1994) and those for C+ from Heiles
(1994).
Recent HST observations indicate that the interstellar abundance of
carbon and nitrogen in
the gas phase is fairly constant on various lines of sight in our Galaxy as
![]() (Sofia et al. 1997) and
(Sofia et al. 1997) and
![]() (Meyer et al.
1997). Based on these values the relative abundance of N to C
will increase by 30%.
The following discussion thus has an uncertainty of this level
associated with the assumed abundance.
(Meyer et al.
1997). Based on these values the relative abundance of N to C
will increase by 30%.
The following discussion thus has an uncertainty of this level
associated with the assumed abundance.
![]() = 120 cm-3.
Petuchowski et al. (1994) reported a large
[N II]122
= 120 cm-3.
Petuchowski et al. (1994) reported a large
[N II]122 ![]() m
to 205
m
to 205 ![]() m line ratio in the central 850 pc of M 82 compared to the
average ratio of the Milky Way (Wright et al. 1991),
indicating that a fair fraction of the [N II] line emission
comes from the ionized gas of
m line ratio in the central 850 pc of M 82 compared to the
average ratio of the Milky Way (Wright et al. 1991),
indicating that a fair fraction of the [N II] line emission
comes from the ionized gas of
![]() -180 cm-3 in M 82.
The ratio of [N II]122
-180 cm-3 in M 82.
The ratio of [N II]122 ![]() m to [C II]158
m to [C II]158 ![]() m of non-PDR
origin for M 82
is about 0.3 in the present analysis, suggesting that there may be a
significant contribution to the [CII] emission from
the low density diffuse ionized gas in the outer part (>850 pc) of the
galaxy. The observed intensity
is compatible with the interpretation that
the non-PDR component of [C II]158
m of non-PDR
origin for M 82
is about 0.3 in the present analysis, suggesting that there may be a
significant contribution to the [CII] emission from
the low density diffuse ionized gas in the outer part (>850 pc) of the
galaxy. The observed intensity
is compatible with the interpretation that
the non-PDR component of [C II]158 ![]() m comes from the
ionized gas that emits [N II]122
m comes from the
ionized gas that emits [N II]122 ![]() m.
m.
![]() by
by
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2828f6.eps}\end{figure}](/articles/aa/full/2001/32/aah2828/Timg92.gif)
![]() m to
[O I]63
m to
[O I]63 ![]() m against
R(60/100).
m against
R(60/100).
![]() m line emission.
Figure 5 indicates that there seems no strong trend in the ratio
of [N II]122
m line emission.
Figure 5 indicates that there seems no strong trend in the ratio
of [N II]122 ![]() m to the non-PDR origin of
[C II]158
m to the non-PDR origin of
[C II]158 ![]() m.
We thus simply assume that the contribution from the ionized gas to
[C II]158
m.
We thus simply assume that the contribution from the ionized gas to
[C II]158 ![]() m
emission is proportional to the [N II]122
m
emission is proportional to the [N II]122 ![]() m intensity.
We take a mean value of Fig. 5 as
m intensity.
We take a mean value of Fig. 5 as
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2828f8.eps}\end{figure}](/articles/aa/full/2001/32/aah2828/Timg100.gif)
![]() m to 12CO (J=1-0) line
intensity is another measure for the diagnosis of PDRs.
m to 12CO (J=1-0) line
intensity is another measure for the diagnosis of PDRs.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2828f9.eps}\end{figure}](/articles/aa/full/2001/32/aah2828/Timg101.gif)