4 Parameter estimation for the eclipsing binary

We used the recently written Eclipsing Light Curve (ELC) code of Orosz & Hauschildt (2000) to fit the basic binary observables of S 1082, namely the light curves in the four filters, the two velocity curves and the observed projected rotational velocities of the two stars Aa and Ab. The blue straggler B in this case is modelled as "third light''. The addition of a constant (in phase) light will reduce the observed relative amplitudes of the light curves. The ELC code uses model atmosphere specific intensities, so the flux from a third star can be self-consistently added to several different bandpasses (i.e. a blue third light star dilutes the B-band light curve of a red binary more than it dilutes the I-band light curve). We mainly used the specific intensities derived from the NEXTGEN models (Hauschildt et al. 1999a, 1999b). A few models were also computed using specific intensities derived from Kurucz (1979) models. Only the photometric data of run 1 were used for the light curve fitting as they form the largest set of homogeneous measurements.

We start by estimating the component masses of the eclipsing binary. Unfortunately, we only have radial velocities near one quadrature phase (poor weather prevented us from observing the opposite quadrature), so the velocity amplitudes of the two curves and the binary systemic velocity will not be as constrained as we would like them to be. We fit sinusoids to each of the velocity curves, fixing the period at the photometric period. For star Aa we find $K_{\rm Aa}=120.8\pm 6.4$ km s^-1, $\gamma_{\rm rel,Aa}=1.7\pm 5.8$ km s^-1, $\phi_{\rm 0,Aa}({\rm spect})=0.747\pm 0.007$, where $\gamma_{\rm rel}$ is the systemic velocity relative to the mean cluster velocity and where $\phi_{\rm0}({\rm spect})$ refers to the phase of maximum velocity. For star Ab we find $K_{\rm Ab}=190.1\pm 12.5$ km s^-1, $\gamma_{\rm rel,Ab}=-2.6\pm 12.5$ km s^-1, $\phi_{\rm0,Ab}({\rm spect})=0.242\pm 0.010$. The errors on the individual velocities were scaled to yield $\chi^2_{\nu}=1$ for each curve, and the error estimates on the fitted parameters were derived using the scaled uncertainties. The phasing of the curves are consistent with expectations, where star Aa has its maximum velocity one fourth of an orbital cycle before the deeper photometric eclipse. Since systemic velocities are consistent with being zero, we will assume the binary is a cluster member and hence has $\gamma_{\rm rel} =0$ km s^-1. In this case we find for star Aa $K_{\rm Aa} =119.1\pm 3.1$ km s^-1 and $\phi_{\rm0,Aa}({\rm spect})=0.748\pm 0.007$, and for star Ab we find $K_{\rm Ab}=190.1\pm 11.6$ km s^-1 and $\phi_{\rm0,Ab}({\rm spect})=0.243\pm 0.010$. Taking the sinusoid fits at face value, we can immediately compute the mass ratio of the binary. We find $Q\equiv M_{\rm Ab}/M_{\rm Aa}=K_{\rm Aa}/K_{\rm Ab}=0.63\pm 0.04$. The minimum masses of the two component stars are then $M_{\rm Aa}\sin^3i=2.01\pm 0.38~M_{\odot}$ and $M_{\rm Ab}\sin^3i=1.26\pm 0.27~M_{\odot}$ (see Table 4 for a summary of the observed parameters of the eclipsing binary).

 

 

Table 4: Observed binary parameters. Aa and Ab refer to the stars in the eclipsing binary. V and B-V are taken from Montgomery et al. (1993).

parameter	value
$P_{\rm phot}$	1.0677971(7)
T0	2 444 643.250(2)
V	11.251
B-V	0.415
$K_{\rm Aa}$ (km s-1)	119.1(3.1)
$K_{\rm Ab}$ (km s-1)	190.1(11.6)
Q	0.63(4)
$\gamma_{\rm Aa}$ (km s-1)	0.0 [fixed]
$\gamma_{\rm Ab}$ (km s-1)	0.0 [fixed]
$M_{\rm Aa}\sin^3i$ ($M_{\odot }$)	2.01(38)
$M_{\rm Ab}\sin^3i$ ($M_{\odot }$)	1.26(27)
$v_{\rm rot,Aa} \sin i$ (km s-1)	56(5)
$v_{\rm rot,Ab} \sin i$ (km s-1)	83(5)

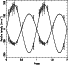Figure 7: Radial-velocity curves of star Aa of the eclipsing binary in S 1082 (filled circles) and star Ab (filled triangles). The lines indicate the best-fitting velocity curves as computed by ELC.

There are a total of twelve free parameters in the model: the filling factors (by radius) of the two stars $f_{\rm Aa}$, $f_{\rm Ab}$, the mean temperatures of the two stars $T_{\rm Aa}$, $T_{\rm Ab}$, the "spin factors'' of the two stars $\Omega_{\rm Aa}$, $\Omega_{\rm Ab}$, where $\Omega$ is the ratio of the rotational angular velocity to the orbital angular velocity, the inclination i, the mass ratio Q, the orbital separation a, the temperature of the third light star $T_{\rm B}$, the surface gravity of the third light star $\log g_{\rm B}$, and the third light scaling factor $SA_{\rm B}$. We assume the orbit is circular, and that the third light star B does not vary. The gravity darkening exponent of star Aa was fixed at 0.25, the standard value for a star with a radiative envelope, while the gravity darkening exponent for star Ab was set at the standard convective value of 0.08. The ELC code uses Wilson's (1990) detailed reflection scheme, and for this problem the albedo of star Aa was taken to be 1 and the albedo of star Ab was taken to be 0.5. Three iterations of the reflection scheme were needed to achieve convergence. Both stars in the binary are assumed to be free of spots. A variation of the "grid search'' routine outlined in Bevington (1969) was used to optimise the fits. In practice the fitting procedure involved a great deal of interaction where some parameters were temporarily fixed at certain values. Several two-dimensional grids in parameter space were defined (for example a grid of points in the $f_{\rm Aa},f_{\rm Ab}$ plane). For each point, we fixed those parameters at the values defined by the grid location and optimised the other parameters, creating contours of $\chi^2$values. New parameter sets were optimised using the set of parameters for a nearby point that gave the best previous fit. After the lowest $\chi^2$ value in a grid was found, then a new grid using other parameters was computed using the best solution as a starting point. The fitting took several weeks of CPU time on an Alpha XP 1000, and sampled a wide range of parameter space. We are reasonably confident that our results are at or very near the global $\chi^2$ minimum.

We found a relatively large number of solutions with similar $\chi^2$values. Figure 6 shows a typical fit. The light curves in the 4 bands (Fig. 6) are fitted reasonably well, although there are still some systematic deviations, especially near the eclipse phases. The radial velocities are also fitted reasonably well (Fig. 7), but again there are some small systematic deviations (the velocity curves seem to be systematically flatter than the sinusoid fits near phase 0.25). In all solutions the binary is detached, i.e. both stars are well within their respective Roche lobes. We applied two additional constraints in order to narrow down the range of parameters. The first constraint is that the total Vmagnitude and B-V colour of the model should match the observed Vmagnitude of S 1082. In this case the apparent V magnitude of the model is easy to compute. We used the synthetic photometry computed from the NEXTGEN models to compute expected absolute V magnitude of each star Aa and Ab in the eclipsing binary from its temperature, radius, and surface gravity. The V magnitude of the blue straggler B then follows from the fitted luminosity scaling. The second constraint is that the implied mass of the blue straggler is roughly consistent with its place in the colour-magnitude diagram. That is, the radius of the blue straggler B can be computed from the distance, the V magnitude, and the temperature. Since the gravity of the blue straggler B is specified in the models, its mass can then be computed. The blue colour of S 1082 requires a relatively hot third light star ($\approx$7500 K), and its surface gravity must be near $\log g=4.25$ in order for the mass to be near $\approx$1.7 $M_{\odot }$. The derived astrophysical parameters for the adopted model are summarised in Table 5. The errors on the parameters were estimated from the $\chi^2$ values generated in the various grid searches. These error estimates may be too small, given the complicated nature of the model. The errors on the masses were taken to be on the order of 15%, as judged from the quality of the sinusoid fits. The light curves of the three components are shown in Fig. 8, and a cartoon of the binary at three phases in Fig. 9.

We have assumed that the stars are not spotted and that the eclipsing binary has a circular orbit. A violation of either one of these assumptions could alter the light curves to produce the small systematic deviations seen in the residuals. Bright or dark spots could either add or remove light at certain phases, complicating the analysis. Given the rather large number of free parameters we have now we did not consider adding spots at this time. If this binary is part of a triple, then the orbit could be eccentric (see Sect. 5). A slight eccentricity ( $e\approx 0.05$ say) could cause the maxima to be asymmetric and the minima to be shifted slightly in phase. Our current velocity curves do not have enough phase coverage to place meaningful constraints on the eccentricity, so any firm conclusions on the eccentricity will have to await the arrival of additional data.

 

 

Table 5: Fitted binary parameters. Aa and Ab refer to the stars in the eclipsing binary, B to the third, outer star.

parameter	Aa	Ab	B
f	0.520(10)	0.700(10)
R ($R_{\odot}$)	2.07(7)	2.17(3)	$\approx$2.5
$R/R_{\rm Roche}$	0.66(7)	0.86(7)
$\Omega$	0.49(5)	0.91(5)
T (K)	6480(25)	5450(40)	7500(50)
log g (cgs)	4.21(2)	4.0(2)	4.25(5)
M ($M_{\odot }$)	2.70(38)	1.70(27)	$\approx$1.7
V	12.33(11)	13.10(11)	12.24(11)
B-V	0.51(2)	0.82(2)	0.33(1)
$i_{\rm A}$ (deg)	64.0(1.0)
$a_{\rm A}$ ($R_{\odot}$)	7.2(4)
V, B-V total	11.30(11), 0.48(2)

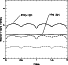Figure 8: Light curves of the three components in S 1082 (dashed-dotted line indicates the primary Aa in the eclipsing binary).

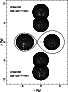Figure 9: Cartoon of the configuration at three orbital phases of the inner binary according to the model listed in Table 5. Note that the Roche-lobes of the two stars Aa and Ab slightly overlap due to the fact that neither star corotates with the orbit.

 

 

Table 6: Times of primary minimum. From left to right: observed time of minimum; O-C difference (in days) between the observed and computed time of eclipse; cycle number of the eclipse with respect to the T₀of Table 4. The errors in the observed times of minimum and the O-C values are 0.005 days.

HJD	O-C	cycle	source
-2 440 000
3191.036	-0.010	-1360	Simoda (1991)a
4643.250	0.000	0	Goranskij et al. (1992)
5325.586	0.013	639	idem
6773.492	-0.013	1995	idem
7861.605	0.014	3014	idem
7920.333	0.014	3069	idem
7944.869	-0.010	3092	idemb
11218.744	-0.001	6158	run 1
11539.078	-0.006	6458	run 2

^a Simoda observed two consecutive primary eclipses. These data were combined to measure one time of minimum.
^b Based on a measurement of a secondary eclipse which we convert to a primary eclipse by adding half a period.
  We note that if the orbit of the eclipsing binary is eccentric, the two eclipses need not be separated by half a period.

Figure 10 shows the decomposition of S 1082 into its components in a colour-magnitude diagram of M 67. Star Ab is located near the 4 Gyr isochrone that provides the best fit to the observed main-sequence, subgiant and giant stars (Pols et al. 1998). Hence the position of star Ab is consistent with the expected value based on its mass. The positions of star Aa and the blue straggler B are a bit more uncertain since one can "trade off'' flux between the two stars (i.e. the blue straggler B can be made brighter at the expense of star Aa in the binary). We note that the star Ab is always located (within the errors) on the 4 Gyr isochrone. The error bars shown on the V magnitudes reflect the uncertainties for our adopted model which produces an overall V magnitude of all three stars close to the observed value. In any event, the hotter star Aa is subluminous by at least 2 mag in V (compare with the track for a 2.2 $M_{\odot }$ star). The position of the blue straggler lies to the red of the extension of the main-sequence as defined by the 1 Myr isochrone.

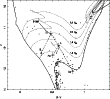Figure 10: Colour-magnitude diagram of M 67 that shows the decomposition of S 1082 into a blue straggler (B) and stars Aa and Ab in the eclipsing binary (A); a dashed line connects their positions. The observed location of S 1082 is indicated with a box; the height of the square equals the depth of the primary eclipse. The dotted lines are evolutionary tracks for 1.6, 1.8, 2.0 and 2.2 $M_{\odot }$ stars corrected for the distance modulus and reddening of M 67 (Z=0.02, Pols et al. 1998). The 4 Gyr-isochrone is included to indicate the expected positions of cluster members; the 1 Myr isochrone is included to give an estimate for the location of the ZAMS (Pols et al. 1998). B and V magnitudes of M 67 stars are from Montgomery et al. (1993). Only stars with a proper-motion membership probability >0.8 (Girard et al. 1989) are plotted.

In order to obtain observed times of primary minimum we use the model light curve as a template to fit the data near the primary minima observed during run 1 and run 2. Seven additional times of minimum are obtained from fitting the data in Table 3 of Goranskij et al. and from the data points of Simoda (1991) (see first column of Table 6). A straight line is fitted to the observed times of minimum to find a new period and T₀ (see Table 4). The period thus derived is compatible with the period listed by Goranskij et al. (Eq. (1)). We use the new ephemeris to compute observed minus computed (O-C) times of primary eclipse and the corresponding cycle number with respect to T₀ (second and third column of Table 6). The peak-to-peak amplitude $\Delta$O-C is $\sim$39 min. If these variations are real and caused by the motion of the eclipsing binary around a third body it would correspond to a minimum semi-major axis in the outer (o) orbit of the binary (b) $a_{\rm o,b}\sin i_{\rm o}=1/2$ c $\Delta$O-C  = 2.3 AU. Assuming that the blue straggler (B) has a mass compatible with its position in the colour-magnitude diagram (about 1.7 $M_{\odot }$) this corresponds to a minimum value of the semi-major axis of the total system $a_{\rm o} \sin i_{\rm o}=a_{\rm o,b}\sin i_{\rm o}~(1+M_{\rm A}/M_{\rm B}) \approx8.4$ AU; combined with the total mass of the system of 6.1 $M_{\odot }$ and Kepler's third law this gives a minimum period of 10 years. This is not compatible with the period of $\sim$3 years found by Milone (1991). We conclude that not all the variation in O-C is due to light-travel time in the outer orbit. There is no evidence for periodicity in the O-C times, although the time baseline is somewhat short and the coverage is somewhat spotty.

Figure 11: O-C times of the primary eclipse in days versus heliocentric Julian date (-2 440 000) of the measurement.