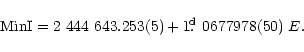 |
(1) |
 |
Figure 1: Light and colour curves for S 1082 folded on the ephemeris of Goranskij et al. (1992). Data from the three runs are indicated with different symbols: open circles for run 1, filled circles for run 2 and triangles for run 3. A typical error bar is shown for each run. Magnitude and colours are plotted relative to the average V(11.25), U-V (0.45), B-V (0.41) and V-I (0.57) values in our measurements. |
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[angle=-90]{fig3.new.ps}}\end{figure}](/articles/aa/full/2001/32/aah2689/Timg23.gif) |
Figure 3:
H |
The spectra of S 1082 are dominated by a narrow-lined component
resembling a star of type early-F. In addition, the presence of a
broad and shallow component in the spectra is
prominent in the H![]() line (see also van den Berg et al. 1999).
When the spectra are arranged in order of light curve phase using
Eq. (1), it is clear that the position and strength of the
asymmetric absorption in the wings vary regularly (Fig. 2);
the spectra that were included in Fig. 8 of van den Berg et al. (1999)
correspond to photometric phases 0.092, 0.16 and 0.25. Around
first quadrature (phase 0.25) the depth of H
line (see also van den Berg et al. 1999).
When the spectra are arranged in order of light curve phase using
Eq. (1), it is clear that the position and strength of the
asymmetric absorption in the wings vary regularly (Fig. 2);
the spectra that were included in Fig. 8 of van den Berg et al. (1999)
correspond to photometric phases 0.092, 0.16 and 0.25. Around
first quadrature (phase 0.25) the depth of H![]() is smallest while
the asymmetric absorption in the wings is maximally blue-shifted; for
phases between 0.5 and 1 the phase-coverage is sparser, but in the
spectra of phases 0.88 and 0.90 it can be seen that the asymmetric
absorption has moved to the red wing. The timing of the velocity shift
with respect to the eclipses associates the broad-lined feature with
the brighter star in the eclipsing binary (the brighter star must
approach us after the primary eclipse). Similar variable line profiles
are visible in the H
is smallest while
the asymmetric absorption in the wings is maximally blue-shifted; for
phases between 0.5 and 1 the phase-coverage is sparser, but in the
spectra of phases 0.88 and 0.90 it can be seen that the asymmetric
absorption has moved to the red wing. The timing of the velocity shift
with respect to the eclipses associates the broad-lined feature with
the brighter star in the eclipsing binary (the brighter star must
approach us after the primary eclipse). Similar variable line profiles
are visible in the H![]() ,
Na I D, Mg I b and
Ca II infrared lines (Fig. 3).
,
Na I D, Mg I b and
Ca II infrared lines (Fig. 3).
The temperature of the narrow-lined star in S 1082 can be measured
with the low-resolution spectra. We assume that its light is least
contaminated by its companion star(s) in the blue and therefore
concentrate on the region around the Balmer jump. In Fig. 4
synthetic spectra for various effective temperatures
![]() are
compared with the IDS spectrum between 3535 Å and 4050 Å. The
spectra were computed with model atmospheres for solar metallicity
(Kurucz 1979). The observed spectrum was corrected for the reddening
towards M 67 (
are
compared with the IDS spectrum between 3535 Å and 4050 Å. The
spectra were computed with model atmospheres for solar metallicity
(Kurucz 1979). The observed spectrum was corrected for the reddening
towards M 67 (
![]() ,
Nissen et al. 1987) and for a
radial-velocity difference with respect to the model spectra. From the
relative strength of the Ca II H&K lines, a sensitive
temperature indicator in this region (e.g. Gray & Garrison 1989),
and the contrast in the Balmer jump it is clear that the observed
spectrum is hotter than that of a 6500 K star.
,
Nissen et al. 1987) and for a
radial-velocity difference with respect to the model spectra. From the
relative strength of the Ca II H&K lines, a sensitive
temperature indicator in this region (e.g. Gray & Garrison 1989),
and the contrast in the Balmer jump it is clear that the observed
spectrum is hotter than that of a 6500 K star.
This part of the spectrum was fitted to model spectra with surface
gravity ![]() ranging from 0.5 to 5.0 in steps of 0.5,
ranging from 0.5 to 5.0 in steps of 0.5,
![]() from 6000 to 8000 K in steps of 250 K and a fixed projected
rotational velocity
from 6000 to 8000 K in steps of 250 K and a fixed projected
rotational velocity
![]() of 10 km s-1. A free
parameter is a wavelength-independent scale factor ranging from 0.025
to 1 in increments of 0.025 that is a measure of the relative
contribution of the narrow-lined star. Observed and model spectra were
normalised to the flux at 4050 Å. A straight line was fitted to the
difference between the observed and each scaled model spectrum. The
model that produces the smallest residuals to the fit has
of 10 km s-1. A free
parameter is a wavelength-independent scale factor ranging from 0.025
to 1 in increments of 0.025 that is a measure of the relative
contribution of the narrow-lined star. Observed and model spectra were
normalised to the flux at 4050 Å. A straight line was fitted to the
difference between the observed and each scaled model spectrum. The
model that produces the smallest residuals to the fit has
![]() K,
K,
![]() and scale factor 0.85. If the temperature
of the hot star is indeed 7500 K, it is a late A rather than an F
star; the value of
and scale factor 0.85. If the temperature
of the hot star is indeed 7500 K, it is a late A rather than an F
star; the value of ![]() is close to that of a main-sequence star
for which
is close to that of a main-sequence star
for which
![]() (Gray 1992). This shows that the
narrow-lined component dominates the spectrum in the blue and it
implies that one of the individual components of S 1082 remains a
blue straggler. A more accurate decomposition of S 1082 is given in
Sect. 4.
(Gray 1992). This shows that the
narrow-lined component dominates the spectrum in the blue and it
implies that one of the individual components of S 1082 remains a
blue straggler. A more accurate decomposition of S 1082 is given in
Sect. 4.
Radial velocities were measured via cross correlation of the
high-resolution spectra with appropriate template spectra
(Table 3). To determine the radial velocities of the
narrow-lined star in S 1082 we adopted as templates spectra of F-type
radial-velocity standards observed during the same run (Table
2). Velocities were derived for each order
separately. Only orders without strong telluric lines were selected,
and included 4890-6820 Å for the 1996-spectra and 4435-6820 Å for the 2000-spectra. The radial velocities listed in the third column
of Table 3 are the averages of the values from the individual
orders; the errors represent the spread around the average. Note that
systematic errors can still be included, e.g. due to the wavelength
calibration. We expect the latter not to exceed 0.75 km s-1 (see
Sect. 2.2.1). Our measurements confirm that the
narrow-lined component in S 1082 shows radial-velocity variations of
only a few km s-1.
The radial-velocity curves of the stars in the eclipsing binary were measured after the contribution of the hot, narrow-lined star to the total spectrum was removed. To that end, all spectra were first brought to the rest frame of the hot star. Then, a hot-star template spectrum was constructed by taking the median of the spectra obtained at phases 0.95, 0.97, 0.0035, 0.019 and 0.048; these particular phases were chosen in order to let the spectral line profiles of the template be as symmetric as possible. For the 1996-spectra, taken with a different instrumental setup, the spectrum obtained at phase 0.092 was chosen as a template. The relative contribution of the hot-star template to the remaining spectra was derived with the same fitting procedure as described in Sect. 3.2: the template multiplied with scaling factors ranging from 0.025 to 1 was subtracted from each individual spectrum, and the scaling that produces the smallest residuals around a fit to a straight line was chosen as the appropriate scaling for that particular spectrum. The scaled template was then subtracted from the total spectrum to obtain the spectrum of the binary at various phases.
Next, these residual spectra were correlated against a synthetic
spectrum of
![]() K and
K and
![]() .
For this model
spectrum we chose
.
For this model
spectrum we chose
![]() km s-1 to roughly match
the apparently broader lines in the spectrum of the binary. This
procedure was repeated for every order between 4380 and 6435 Å,
excluding the order that contains the broad H
km s-1 to roughly match
the apparently broader lines in the spectrum of the binary. This
procedure was repeated for every order between 4380 and 6435 Å,
excluding the order that contains the broad H![]() line and the
region between 5690 and 6090 Å for which the cross correlation functions
are very noisy with no clear peaks. A cross correlation peak is
sometimes visible at
line and the
region between 5690 and 6090 Å for which the cross correlation functions
are very noisy with no clear peaks. A cross correlation peak is
sometimes visible at
![]() km s-1 and represents
features of the hot star that were not corrected for (or introduced
into the spectrum) by subtraction of the template. The cross
correlation functions of most spectra clearly show two peaks with a
variable separation (see Fig. 5). One peak is smaller and
broader than the other, and is redshifted with respect to the template
for phases smaller than 0.5; therefore, this peak is identified with
the secondary star in the eclipsing binary. This is the first
spectroscopic evidence for the third star in S 1082. The
measurements of the velocity of the primary near phase 0.1 are
probably distorted due to its eclipse by the secondary star. In the
following we will refer to the components of the eclipsing binary as
Aa and Ab, and to the outer companion as B.
km s-1 and represents
features of the hot star that were not corrected for (or introduced
into the spectrum) by subtraction of the template. The cross
correlation functions of most spectra clearly show two peaks with a
variable separation (see Fig. 5). One peak is smaller and
broader than the other, and is redshifted with respect to the template
for phases smaller than 0.5; therefore, this peak is identified with
the secondary star in the eclipsing binary. This is the first
spectroscopic evidence for the third star in S 1082. The
measurements of the velocity of the primary near phase 0.1 are
probably distorted due to its eclipse by the secondary star. In the
following we will refer to the components of the eclipsing binary as
Aa and Ab, and to the outer companion as B.
| HJD- | phot. |
|
|
|
| 2 450 000 | phase | km s-1 | km s-1 | km s-1 |
| 142.5101 | .09213 |
|
- | - |
| 142.5790 | .1567 |
|
- | |
| 142.6837 | .2548 |
|
- | |
| 1591.3642 | .9540 |
|
- | - |
| 1591.3822 | .9709 |
|
- | - |
| 1591.4170 | .003451 |
|
- | - |
| 1591.4334 | .01880 |
|
- | - |
| 1591.4640 | .04750 |
|
- | - |
| 1591.4805 | .06294 |
|
- | - |
| 1591.4967 | .07812 |
|
||
| 1591.5452 | .1235 |
|
||
| 1591.5616 | .1389 |
|
||
| 1591.5779 | .1541 |
|
||
| 1591.5993 | .1742 |
|
||
| 1591.6150 | .1890 |
|
||
| 1591.6310 | .2039 |
|
||
| 1591.6474 | .2192 |
|
||
| 1591.6682 | .2387 |
|
||
| 1591.6840 | .2535 |
|
||
| 1591.7010 | .2695 |
|
||
| 1617.4072 | .3435 |
|
||
| 1617.4308 | .3656 |
|
||
| 1617.6147 | .5378 |
|
- | |
| 1617.6394 | .5609 |
|
- | - |
| 1624.3903 | .8832 |
|
||
| 1624.4092 | .9009 |
|
||
| 1624.5766 | .05765 |
|
- | - |
| 1624.5949 | .07484 |
|
||
| 1624.6131 | .09188 |
|
We used the spectrum observed near first quadrature (wavelength region
5160 to 5240 Å containing the Mg I b triplet) to derive an
estimate for the projected rotational velocities of both components
from the widths of their cross correlation peaks. To that end, we
cross correlated a synthetic spectrum of a certain temperature (
![]() ,
,
![]() km s-1) with synthetic templates
of the same temperature and surface gravity with
km s-1) with synthetic templates
of the same temperature and surface gravity with
![]() ranging from 10 to 100 km s-1, and with the object spectrum. The
peak of the cross correlation functions were fitted with Gaussian
profiles. This was repeated for synthetic spectra of temperatures 5000
to 6750 K in steps of 250 K. With the results we constructed calibration
curves for each temperature that give the width of the cross
correlation peak as a function of the projected rotational velocity of
the synthetic template. The widths of the cross correlation peaks from
the object spectrum then give a rough estimate for the
ranging from 10 to 100 km s-1, and with the object spectrum. The
peak of the cross correlation functions were fitted with Gaussian
profiles. This was repeated for synthetic spectra of temperatures 5000
to 6750 K in steps of 250 K. With the results we constructed calibration
curves for each temperature that give the width of the cross
correlation peak as a function of the projected rotational velocity of
the synthetic template. The widths of the cross correlation peaks from
the object spectrum then give a rough estimate for the
![]() of both stars. For star Aa we obtain a
of both stars. For star Aa we obtain a
![]() of 51 km s-1 (5750 K) to 58 km s-1 (6750 K), for star Ab
a
of 51 km s-1 (5750 K) to 58 km s-1 (6750 K), for star Ab
a
![]() of 83 km s-1 (5500, 5750 K) to 87 km s-1 (6750 K).
of 83 km s-1 (5500, 5750 K) to 87 km s-1 (6750 K).
![\begin{figure}
\par\includegraphics[width=13.3cm]{H2689f6.ps}\end{figure}](/articles/aa/full/2001/32/aah2689/Timg100.gif) |
Figure 6: Fit to the light curves in the U, B, V and Gunn i band. The small panels show the residuals to the fit. Only the data from the first observation run are used. |
Copyright ESO 2001