For a radio source to be included in our sample, it must be larger than
![]() and it must have been noticed on the radio maps as a large radio
source. The latter is related to a surface brightness
criterion: the average
surface brightness, or integrated signal-to-noise ratio, must be high
enough to be detected as a single radio source structure. The integrated signal-to-noise ratio,
and it must have been noticed on the radio maps as a large radio
source. The latter is related to a surface brightness
criterion: the average
surface brightness, or integrated signal-to-noise ratio, must be high
enough to be detected as a single radio source structure. The integrated signal-to-noise ratio,
![]() ,
for a resolved radio source is given by
,
for a resolved radio source is given by
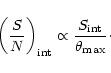 |
(2) |
The sensitivity limit appears to be almost independent of angular
size at least up to a size of ![]() arcmin.
The sensitivity of WENSS to objects with an
angular size above 1 degree on the sky decreases, so that the sensitivity
limit inevitably must rise eventually.
arcmin.
The sensitivity of WENSS to objects with an
angular size above 1 degree on the sky decreases, so that the sensitivity
limit inevitably must rise eventually.
From the figure we conclude that sources with
![]() will most likely be selected
if
will most likely be selected
if
![]() Jy/arcmin. We will use this
criterium to specify the regions in the radio power - linear size -
redshift (P,D,z) parameter space which is accessible by our selection.
Jy/arcmin. We will use this
criterium to specify the regions in the radio power - linear size -
redshift (P,D,z) parameter space which is accessible by our selection.
In Fig. 3 we have plotted for all identified GRGs in our sample the linear size, D, against the radio power at 325 MHz, P, the so-called P-D diagram. For reference, all sources of the LRL sample with z < 0.6, which is the same redshift range as in which the GRGs are found, are plotted as well. Note that several of the formerly known GRGs are part of the LRL sample; these have been plotted as LRL sources.
From this plot the following can be concluded. First, although we have conducted the most extensive systematic search for GRGs to date, there are no sources in the upper right part of the P-D diagram, i.e. the region occupied by sources with large size and high radio power. If such sources had existed in our search area, They would most likely have discovered because of their inevitable high flux density. Second, the few GRGs which have a linear size above 2 Mpc have, on average, a higher radio power than smaller-sized GRGs.
To investigate which region of the P-D diagram is accessible
through our WENSS selection, we have plotted in
Fig. 4 lines which represent the lower sensitivity
limit at constant redshift. Since the sensitivity limit is set by
![]() Jy/arcmin (see Sect. 5.1), and a given redshift
Jy/arcmin (see Sect. 5.1), and a given redshift
![]() and
and
![]() ,
the limit at that redshift follows the
relation
,
the limit at that redshift follows the
relation
![]() .
In Fig. 4 we have assumed a radio
source spectral index of -0.8 to convert flux density into radio power.
.
In Fig. 4 we have assumed a radio
source spectral index of -0.8 to convert flux density into radio power.
At a particular redshift, WENSS can only detect giant sources which are more powerful than the radio power at which the line has been drawn (i.e. only in that part of the P-D diagram which is situated above the line).
Note that lines of higher redshifts also start at a larger
linear size because of the
![]() lower angular size limit we have
imposed. Based on the accessible regions in the P-D diagram there is no apparent reason why sources larger than 2 Mpc should be missed.
lower angular size limit we have
imposed. Based on the accessible regions in the P-D diagram there is no apparent reason why sources larger than 2 Mpc should be missed.
In Fig. 5a we have plotted the 325-MHz radio powers of the GRGs against their redshifts. The higher sensitivity of the WENSS, as compared to earlier surveys, has enabled the discovery of GRGs with 5-10 times lower radio power. The hatched region in the figure indicates the part of the parameter space which is not accessible by WENSS, as a result of its limited sensitivity and lower angular size limit. Again, in determining this region we have assumed a spectral index of -0.8 for the radio sources, but the upper edge of the region is not very sensitive to the spectral index.
The broken shape of the upper edge of the hatched region can be understood as
follows. At all redshifts, the WENSS is most sensitive to physically,
and thus spatially, small sources. Since both a lower
angular and physical size limit have been imposed, there are two regimes in which each of
these two limits is in effect. At very low redshifts,
a source with a physical size of 1 Mpc extends over
![]() on the sky. This leads to a surface brightness limit
and the integrated flux density of the source thus has to be large for the source to be still detectable. At higher
redshift, the selection is constrained by the
on the sky. This leads to a surface brightness limit
and the integrated flux density of the source thus has to be large for the source to be still detectable. At higher
redshift, the selection is constrained by the
![]() lower
angular size limit. This results in a lower limit to the flux
density of a detectable source, determined by
lower
angular size limit. This results in a lower limit to the flux
density of a detectable source, determined by
![]() Jy. Thus, we
are flux density limited. The break occurs
at that redshift at which a 1-Mpc large radio source will span
an angle of
Jy. Thus, we
are flux density limited. The break occurs
at that redshift at which a 1-Mpc large radio source will span
an angle of
![]() on the sky (
on the sky (
![]() ).
).
The one source that just lies in the hatched area where no sources should have been found is B1044+745, which, as mentioned before, would indeed not have been selected on basis of the WENSS data.
The strong effect that the lower angular size limit has on the
selection can best be seen in Fig. 5b, where we
have plotted the projected linear size of the identified GRGs against their
redshift. Again, the hatched area indicates the region of the diagram which is
inaccessible. The strong "bump'' at redshifts above
![]() result from the lower angular size limit.
result from the lower angular size limit.
Furthermore, in Fig. 5b we have plotted the sensitivity limit for sources of constant radio power (dashed lines). The (logarithm of the) radio power (in WHz-1 at 325 MHz) for each particular line has been indicated at the top of the diagram. A radio source of radio power P and linear size D can only be selected if it has redshift below that indicated by the dashed line for power P at size D. Had that source been at a higher redshift, or had it been of larger linear size, it would not have been selected. Likewise, all sources which lie on the left of such a line of constant P, should all have a radio power below this value. Apart from the before-mentioned case of B1044+745, this is indeed the case for the identified GRGs in our sample.
A strong drop in the number of sources with projected linear size above 2 Mpc has been found (see Fig. 1c). This may be a result of a strong negative radio power evolution of radio sources with increasing size, combined with our sensitivity limit. A negative radio power evolution is indeed expected for active radio radio sources (cf. Kaiser et al. 1997; Blundell et al. 1999). On the other hand, the observed effect can also be caused if a substantial fraction of the GRGs stop their radio activity (and "fade'') before they reach a size of 3 Mpc.
Above, we have argued that the selection effects alone provide no apparent reason why sources of linear size above 2 Mpc should have been missed if they existed in large numbers. On the contrary, Fig. 5b shows that sources above 2 Mpc in size can potentially be selected out to much higher redshift than smaller sized sources. Indeed, the figure shows that the majority of identified 2-3 Mpc large sources have redshifts at which 1-Mpc large sources would not have been selected.
Therefore, the observed 2-Mpc cut-off must be caused by a combination of the internal luminosity evolution of the sources and the sensitivity of the WENSS. An extreme case of such a luminosity evolution occurs when a large fraction of giant sources do not remain active for a long enough amount of time to reach a linear size of 2 Mpc. To disentangle the effects of the luminosity evolution of active and so-called "relic'' sources on the observed number of sources as a function of linear size requires much better statistics on the death-rate of radio galaxies as a function of radio power and linear size.
Acknowledgements
The INT and WHT are operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias. The Westerbork Synthesis Radio Telescope (WSRT) is operated by the Netherlands Foundation for Research in Astronomy (NFRA) with financial support of the Netherlands Organization for Scientific Research (NWO). The National Radio Astronomy Observatory (NRAO) is operated by Associated Universities, Inc., and is a facility of the National Science Foundation (NSF). This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. The Digitized Sky Surveys were produced at the Space Telescope Science Institute under U.S. Government grant NAG W-2166. The images of these surveys are based on photographic data obtained using the Oschin Schmidt Telescope on Palomar Mountain and the UK Schmidt Telescope. The plates were processed into the present compressed digital form with the permission of these institutions. M. N. Bremer, H. Sangheera and D. Dallacasa are thanked for their help in the early stages of this project. P. Best and M. Lehnert are thanked for many helpful discussions and suggestions. L. Lara is acknowledged for providing high resolution radio maps of several sources prior to publication.
Copyright ESO 2001