In this section we will describe the photometric data available and how we use this to obtain realistic estimates of the mass of the stellar populations in the target galaxies.

For most of the galaxies we have extensive optical and near infrared images and, in addition, photo-electric photometry (Bergvall & Olofsson 1986; Bergvall & Olofsson private correspondence). These data have been collected at the ESO telescopes on La Silla. The available photometry for each galaxy is shown in Table 2.

The luminosity profiles have been derived by integrating in elliptical rings, using the same position angle and inclination as derived from the kinematical data. The luminosity profile software was written in Uppsala and is described in Bergvall & Östlin (2001), where the photometric properties of several of the galaxies in the present study is discussed at length.

The luminosity profile of a galaxy traces the spatial distribution of its stars. In the ideal case of a uniform stellar population with no extinction, the surface brightness directly reveals the stellar mass density. However if the mass to luminosity ratio of the stellar population varies, e.g. due to star formation, there will be no simple relation between the observed luminosity distribution and the real mass distribution of stars.

In BCGs this problem is serious because, in general, the starburst population dominates the emission of light, but not the mass. Furthermore, since the fraction of old stars is a priori unknown (especially in the starburst region) and the starburst has a rapid luminosity evolution, the mass to light ratio of the stellar population is very uncertain and varies with galacto-centric distance. In general, the starburst region is close to the optical centre of a BCG. In the outskirts M/Lmay be above one, while in the youngest region of the burst it should be much lower. To make progress we have taken the following approach.

By looking at the radial colour profiles, we determine the extent of the starburst. In the outskirts the colours are stable (see Fig. 1), indicating that the assumption of a homogeneous stellar population is plausible here. Therefore, the luminosity profile of each galaxy was decomposed into two components, a disk and a burst. The disk component has little or no colour gradient and is interpreted as the underlying, older, population. It has been produced from an exponential fit to the luminosity profile (usually in the V-band) at radii where the colours were stable, and, if possible, comparable to the radius of the last measured point in the rotation curves. In all cases, an exponential law provides a good fit to the data at these radii. The residual after subtracting the disk component, we call the burst component. The true photometric structure of the galaxies at larger radii may be more complicated (Bergvall & Östlin 2001), but this is not of concern here since we are only interested in estimating the mass of the stellar population within the extent of the rotation curves. An example of the photometric decomposition is shown in Fig. 1. Note how the colours stabilise at the same radius as the disk takes over from the burst as the main contributor to the emitted light. This is the typical situation in the sample studied here. A representative choice of colour indices for the disk and the subtracted burst components are shown in Table 2. Multi-wavelength colour profiles for all galaxies, except ESO 185-13 and Tololo 0341-407, are presented in Bergvall & Östlin (2001).

2.2 Internal extinction

BCGs in general have low internal extinction (e.g. Mas-Hesse & Kunth 1999), which probably is a consequence of low chemical abundances and selection criteria that favour galaxies with blue colours. The central E(B-V) values derived spectroscopic observations of the H $\alpha/$ H $\beta$ ratio and Case B recombination are given in Table 2. In some cases, these could be overestimated due to underlying Balmer absorption from young A-type and old stars. Long slit spectra (Bergvall & Östlin 2001) indicate that the H $\alpha/$ H $\beta$ ratio decreases with radius. Moreover, investigations including the UV-continuum suggest that the emission lines are more heavily reddened than the stellar continuum (Calzetti et al. 1994; Mas-Hesse & Kunth 1999). Hence, applying the E(B-V) values in Table 2 throughout would overestimate the internal extinction. We have used the values given in Table 2 for the central of the galaxies and assumed that the extinction coefficient scales with the thickness of the disk, i.e. the surface brightness. In effect, the adopted extinction for the burst component is close to the values given in Table 2, whereas the extinction for the disk component is significantly smaller. In any case, the reddenings in Table 2 are small and the uncertainty in the disk E(B-V) values do not seriously affect the derived photometric masses, as we argue below.

2.3 Spectral evolutionary synthesis models

We use a spectral evolutionary synthesis model in combination with colour profiles in the optical and near infrared to estimate the mass-to-light ratios of the galaxies. The model used has been developed by Bergvall and is described in Bergvall & Rönnback (1995), Östlin et al. (1998) and Bergvall & Östlin (2001). Briefly, it is based on stellar evolutionary tracks from the Geneva group (Schaller et al. 1992), mostly Kurucz (1992) model atmospheres, and a nebular emission component from Cloudy (Ferland 1993). Moreover, pre-main sequence stage evolution from VandenBerg (1985; private correspondence 1986), and horizontal branch and AGB stages up to the onset of thermal pulsations from Castellani et al. (1991), have been included. Empirical data are used to extend the evolution to the tip of the AGB. Most of the galaxies have determined nebular oxygen abundances, which are close to 1/10th of solar (Bergvall & Östlin 2001; Masegosa et al. 1994). This value was therefore used for the stellar and gaseous components in the spectral evolutionary synthesis model. The used model parameters are summarised in Table 1.

The model also calculates M/L_V, the V-band mass to light ratio for the stellar population. This includes the mass of stellar remnants, and the gas returned to the interstellar medium. Counting only the mass of stars and remnants would result in slightly lower M/L values. What matters is to what extent the returned gas is used for new star formation. Since these galaxies have low metallicity their ISM are not heavily polluted and the returned gas will be diluted before any of it is taken up in new stars. Hence it is justified to include the returned gas in the mass budget for calculating M/L.

The models by Bergvall, described in Table 1, were complimented with models produced with the PEGASE.2 code (Fioc & Rocca-Volmerange 1999), to check consistency and to further explore the parameter space. In particular, models with shorter star formation time-scales (instantaneous burst and e-folding times of 10, 30 and 100 Myr) were used to constrain the properties of the central "burst'' regions.

**Table 1:** Spectral evolutionary synthesis model parameters used in M/L determinations. The IMF slope is defined as dN/d $M \propto M^{-\alpha }$ , where Mis the stellar mass and dN is the number of stars in the mass interval $[M, M+{\rm d}M]$ . The classical value by Salpeter (1955) is $\alpha = 2.35$ .
IMF slope $\alpha$	2.0, 2.35 and 2.70
Lower mass limit $M_{\rm low}$	0.1 and 1.0 $M_{\odot }$
Upper mass limit $M_{\rm up}$	30 and 100 $M_{\odot }$
Burst duration $\tau$	50 and 16000 Myr
SFR e-folding time $\beta$	0 and 3 Gyr
Metallicity	$0.1~Z_{\odot}$

Table 2: Available photometry and adopted V-band M/L ratios.
Galaxy E(B-V) Photometry Disk/Burst colours Disk colour $M/L_{\rm disk}$ $M/L_{\rm disk}^{\rm min}$ $M/L_{\rm disk}^{\rm max}$ $M/L_{\rm burst}$

(1) (2) (3) (4) (5) (6) (7) (8) (9)

ESO 350-38 $\le$ 0.25 BVRIJHK B-V = 0.5 / 0.3 V-J = 1.9 3.0 2.0 6.0 0.05

ESO 480-12 $\le$ 0.30 BVRIJHK B-V = 0.3 / 0.0 V-J = 1.6 2.3 1.6 3.6 0.06

ESO 338-04 $\le$ 0.06 BVRIJHK B-V = 0.3/ 0.2 V-J = 1.7 3.0 2.1 3.8 0.05

ESO 338-04B $\le$ 0.06: VIJHK V-I = 0.7 / 0.0 V-J = 1.6 3.4 2.5 6.0 0.10

ESO 185-13 $\le$ 0.16 U^aB^aVRI^a V-R = 0.4 / 0.2 2.2 1.0 6.0 0.08

ESO 400-43 $\le$ 0.22 BVRIJHK B-V = 0.9 / -0.2 V-J = 1.6 3.1 2.2 6.5 0.06

ESO 400-43B $\le$ 0.17 BV^aRI^aJHK B-R = 0.8 / 0.4 B-J = 2.3 3.0 1.0 4.0 0.10

Tol 0341-403E $\le$ 0.24 R 3.0: 1.0: 6.0: 0.03

Tol 0341-403W $\le$ 0.29 R 3.0: 1.0: 6.0: 0.05

**Table 2:** Available photometry and adopted V-band M/L ratios.
Galaxy	E(B-V)	Photometry	Disk/Burst colours	Disk colour	$M/L_{\rm disk}$	$M/L_{\rm disk}^{\rm min}$	$M/L_{\rm disk}^{\rm max}$	$M/L_{\rm burst}$
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
ESO 350-38	$\le$ 0.25	BVRIJHK	B-V = 0.5 / 0.3	V-J = 1.9	3.0	2.0	6.0	0.05
ESO 480-12	$\le$ 0.30	BVRIJHK	B-V = 0.3 / 0.0	V-J = 1.6	2.3	1.6	3.6	0.06
ESO 338-04	$\le$ 0.06	BVRIJHK	B-V = 0.3/ 0.2	V-J = 1.7	3.0	2.1	3.8	0.05
ESO 338-04B	$\le$ 0.06:	VIJHK	V-I = 0.7 / 0.0	V-J = 1.6	3.4	2.5	6.0	0.10
ESO 185-13	$\le$ 0.16	U^aB^aVRI^a	V-R = 0.4 / 0.2		2.2	1.0	6.0	0.08
ESO 400-43	$\le$ 0.22	BVRIJHK	B-V = 0.9 / -0.2	V-J = 1.6	3.1	2.2	6.5	0.06
ESO 400-43B	$\le$ 0.17	BV^aRI^aJHK	B-R = 0.8 / 0.4	B-J = 2.3	3.0	1.0	4.0	0.10
Tol 0341-403E	$\le$ 0.24	R			3.0:	1.0:	6.0:	0.03
Tol 0341-403W	$\le$ 0.29	R			3.0:	1.0:	6.0:	0.05

Description of column contents: (1) Name of galaxy. (2) The central E(B-V) derived from spectroscopy. The source is Bergvall & Östlin (2001), except for ESO 185-13 (Calzetti et al. 1994) and Tololo 0341-403 (Terlevich et al. 1991). For E338-04B no spectroscopic E(B-V) was available and we used the same value as for ESO 338-04, and flagged it with a colon (:). (3) Available photometry. Entries with superscript ^a indicates that for this filter only aperture photometry is available. (4) Representative optical colours for the disk and burst regions, corrected for extinction (see Sect. 2.2). B and V are in the Johnson filter system, R and I in the Kron-Cousins filter system. Typical errors are 0.1 or less for the disk, and slightly larger for the burst components. (5) Representative optical-near infrared colour for the disk components, errors 0.2-0.3. (6) shows the best fitting M/L_V values (in solar units) for the disk component. (7) and (8) show the 3 $\sigma$ upper and lower limits on the disk M/L_V, respectively. The uncertain M/L_V values for Tololo 0341-403 are indicated with colon, see text for further explanation. (9) Best fitting M/L_V estimate for the burst component.

2.4 M/L values

The ensemble of model predictions characterised in Table 1 were compared to the observed broad-band colours of the galaxies. The colours of the disk and burst components where modelled separately. Taking the observational uncertainties into account, we determine which models reproduce the disk colours within $\sim$ $3 \sigma$ and read off their M/L value. Some models were discarded because they give unreasonable M/L values at certain ages, e.g. short burst models with lower mass limit $M_{\rm low} = 1~M_\odot$ and ages larger than a few Gyr. Such models are in any case not very realistic. Apart from this, the best-fitting M/L is generally well defined, as is also the minimum allowed M/L value. The upper limit to the M/L value is generally less well constrained.

In many cases there is a "good degeneracy'', in the sense that while the best fitting age is sensitive to the choice of model parameters, the corresponding M/L values are very similar. We illustrate this with the following example: Compared to a standard $\alpha = 2.35$ model, a model with a steeper $\alpha = 2.85$ IMF, will for each time-step have redder colours and higher M/L. Fitting a galaxy's colour to this steep IMF model will produce a lower age, and this will to first order compensate for the change in M/L. The same effect occurs if one varies the metallicity. Similarly, increasing the assumed E(B-V) value decreases the modelled age and M/L but this effect is to a first order compensated by the increasing amount of absorbed emission to correct for.

In this paper, we have only considered single power-law IMFs. The use of broken power-law IMFs with two or more segments (e.g. Miller & Scalo 1979; Kroupa et al. 1993; Scalo 1986, 1998) could decrease the modelled M/L values somewhat, up to a factor of 2 at large ages. Hence, if the IMF in our galaxies has a flatter low mass range, the real M/L values would approach the lower limits given in Table 2. On the other hand, the possible extension of the IMF to objects with sub-stellar masses would increase M/L by $\sim$ 10% for an IMF with relatively flat slope in the regime below 1 $M_{\odot }$ .

In general, models with $M_{\rm low} = 0.1$ $M_{\odot }$ , $M_{\rm up} = 100$ $M_{\odot }$ , $\alpha = 2.35$ and a continuous but exponentially decaying ( $\beta = 3$ Gyr) star formation rate give the best fit to the observed colours of the disk component. The best fitting ages are found between 2.5 and 8 Gyr for the different galaxies (between 1 and 16 Gyr considering the lower and upper 3 $\sigma$ limits). Of course there might be even older components present, that however cannot make a significant contribution to the mass within the modelled radii. The age of the halo stellar populations is further discussed in Bergvall & Östlin (2001). The resulting M/L values for the disk component are shown in Table 2. For ESO185-13, we have only optical surface photometry in V and R and no near-IR data and consequently its $M/L_{\rm disk}$ values are less certain. For one galaxy (Tololo 0341-407), we did not have multicolour data, and instead we used the median value $M/L_{\rm disk}$ for the other galaxies, and the extreme of $M/L_{\rm disk}^{\min}$ and $M/L_{\rm disk}^{\max}$ for the allowed range; these values are flagged with a colon (:) in Table 2.

It was more difficult to constrain the M/L values for the burst components, since there is a large dependence on model parameters and strong colour gradients. Moreover, ionised gas emission is important and may be non-local, i.e. the emitting gas is displaced with respect to the ionising source and e.g. found in filaments (Östlin et al. 1998). The contribution of line and continous emission from ionised gas has the effect of making the burst colours presented in Table 2 redder. Part of the difficulty may arise because the burst population is not completely coeval, but includes a mix of stars with ages differing up to several 10 Myrs. For the burst, we used also the observed H $\alpha$ equivalent-widths to constrain its age and M/L. We were able to constrain that in all cases 0.01 < M/L < 0.2, except when using a very steep IMF ( $\alpha \ge 3.0$ ), which however gives worse fits to the data. We have used the values given in Table 2 as our estimates for the burst, with a generous allowed interval of M/L=0.01 to M/L=0.4, common for all galaxies. Within this range in M/L, the burst always make a minor contribution to the total photometric mass.

2.5 Star formation rates and time-scales

With the aid of the spectral synthesis code described in Sect. 2.2, the integrated H $\alpha$ luminosities have been used to derive the total star formation rates in the observed galaxies. For a Salpeter IMF with mass range $0.1{-}100~M_\odot$ , and with $L({\rm H}\alpha)$ in Watts, the SFR expressed in $M_{\odot}/{\rm yr}$ is:

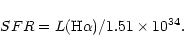
Together with the photometric and rotational mass estimates the integrated SFR estimates can be used to derive mass averaged values. In Table 4 we give the SFR normalised to the photometric galaxy masses. The normalisation using rotational mass would in some cases (when there is an apparent dynamical mass deficiency) overestimate the mass averaged SFR, and this quantity is not presented explicitly.

The inverse of the mass averaged SFRs also provide $\tau_{\rm ph}$ , the time scale for building up the observed photometric mass in stars with the current SFR. In general, $\tau_{\rm ph}$ is close to 1 Gyr, meaning that the current SFR is one order of magnitude larger than the average past SFR. Thus, these galaxies are true star bursts in the sense that their SFR is an order of magnitude higher than what is sustainable over a Hubble time. Note that the modelling in Sect. 2.3 indicate ages of several Gyrs for the underlying populations. For the two companions we find larger values of $\tau_{\rm ph}$ . In the eastern component of Tololo0341-407 $\tau_{\rm ph} \sim 0.25$ Gyr, indicating a momentary very enhanced SFR, although its photometric mass is quite uncertain.

Similarly, we can define $\tau_{\rm b} = M_{\rm burst}/SFR$ , the time scale for building up the observed burst mass. Hence $\tau_{\rm b}$ gives an order of magnitude estimate of how long the present burst has been active. Values of $\tau_{\rm b}$ are given in Table 4. If the SFR has passed its peak, $\tau_{\rm b}$ will overestimate the burst duration. In ESO338-IG04 we find $\tau_{\rm b} \sim 50$ Myr, in good agreement with the burst duration derived from the age distribution of young star clusters resolved with the HST (Östlin et al. 1998).

Since we corrected for extinction in deriving $M_{\rm ph,26}$ and $M_{\rm burst}$ , but not when deriving the SFR, the timescales $\tau_{\rm ph}$ and $\tau_{\rm b}$ may be slightly overestimated, by up to a factor of two.

Another time scale can be constructed for those galaxies where the H I content is known, i.e. the gas consumption time scale. All galaxies in the sample have determined H I-masses or upper limits. The gas consumption time scale ranges from the extreme value of 5 Myr (sic) for ESO350-IG38 (which has an upper limit of $M_{\rm HI} < 10^8$ $M_{\odot }$ , but see Sect. 4.1) to $\sim$ 3 Gyr for the companion of ESO400-G43. All BCGs have gas consumption time-scales smaller than 1 Gyr, showing that the present SFRs are unsustainable.

**Table 3:** Absolute magnitudes, and mass estimates of disk and burst components.
Galaxy	R	Disk	Burst	${ M}_{\rm disk}$	$M_{\rm burst}$	${ M}_{\rm ph}$	$M_{\rm rot}$	Note
	kpc	M_V	M_V	${10^9~M_{\odot}}$	${10^9~M_{\odot}}$	${10^9~M_{\odot}}$	${10^9~M_{\odot}}$
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
ESO 350-IG38	6.0	-19.3	-20.4	13 _-4.4⁺¹³	0.64 _-0.51^+4.5	13.9 _-4.9⁺¹⁸	0.87 _-0.60^+2.1	$R_{\max}$ , non decomp.
''	0.4	-15.8	-15.4	0.51 _-0.17^+0.51	0.006 _-0.005^+0.050	0.52 _-0.18^+0.56	0.60 _-0.40^+0.90	$V_{\max}$ , non decomp.

''	5.2	-19.2	-20.4	13 _-4.2⁺¹³	0.64 _-0.52^+4.5	13 _-4.7⁺¹⁷	1.6 _-1.1^+3.2	DVF: 1st comp.

''	1.0	-17.3	-18.1	2.1 _-0.7^+2.1	0.078 _-0.062^+0.54	2.1 _-0.75^+2.6	1.3 _-0.90^+5.6	DVF: 2nd comp.

ESO 480-IG12	5.9	-18.4	-19.2	4.6 _-1.4^+2.6	0.25 _-0.21^+1.4	4.8 _-1.6^+4.0	17 _-8.2⁺¹⁷	$R_{\max}$

ESO 338-IG04	2.5	-17.3	-19.0	2.2 _-0.65^+0.58	0.17 _-0.14^+1.2	2.3 _-0.80^+1.8	0.57 _-0.50^+1.8	masked $R_{\max}$

''	1.9	-17.0	-19.0	1.6 _-0.5^+0.4	0.17 _-0.14^+1.2	1.8 _-0.62^+1.6	0.86 _-0.70^+2.0	masked $V_{\max}$

ESO 338-IG04B	3.6	-17.7	-16.4	2.8 _-0.75^+2.2	0.032 _-0.03^+0.10	2.9 _-0.78^+2.3	5.7 _-2.9^+6.0	$R_{\max}$

ESO 185-IG13	3.8	-18.7	-18.7	5.6 _-3.1^+9.7	0.21 _-0.18^+0.85	5.8 _-3.3⁺¹¹	1.5 _-0.90^+1.9	$R_{\max}$

ESO 400-G43	10.9	-19.2	-20.0	12 _-3.4⁺¹³	0.52 _-0.43^+2.9	12 _-3.9⁺¹⁶	0.29 _-0.20^+0.70	$R_{\max}$

''	5.7	-18.9	-20.0	9.9 _-2.9⁺¹¹	0.50 _-0.42^+2.9	10 _-3.3⁺¹⁴	0.66 _-0.50^+1.1	Both

''	1.1	-16.9	-18.2	1.6 _-0.46^+1.7	0.094 _-0.078^+0.53	1.7 _-0.54^+2.3	0.60 _-0.30^+0.70	$V_{\max}$

ESO 400-G43B	4.8	-17.9	-18.1	3.6 _-2.4^+1.2	0.15 _-0.14^+0.46	3.8 _-2.6^+1.7	3.3 _-1.5^+2.1	$R_{\max}$

Tololo 0341-403E	1.6	-14.6	-15.9	0.17 _-0.12^+0.17	0.006 _-0.004^+0.073	0.18 _-0.12^+0.25	0.17 _-0.1^+0.5	Both

Tololo 0341-403W	1.9	-15.6	-16.5	0.43 _-0.29^+0.43	0.018 _{- 0.014}^+0.12	0.45 _-0.30^+0.56	0.26 _-0.20^+0.50	Both

Description of column contents: (1) Name of galaxy (2) Radius (in kpc) within which the properties in Cols. 3 to 8 have been evaluated. (3) Absolute V-band magnitude of disk component. (4) Absolute V-band magnitude of burst component. (5) Estimated photometric mass of the disk component. (6) Estimated photometric mass of the burst component. (7) Total photometric mass of the disk+burst component. (8) Rotational mass. The quoted uncertainties reflect the uncertainty in: the parameter f, the inclination and the rotational velocity, see Paper I. (9) Comments: for some galaxies we present mass estimates at more than one radii, corresponding to certain features in the rotation curve (see Paper I). " $R_{\max}$ '' and " $V_{\max}$ '' means that the mass was evaluated at the last measured point in the rotation curve, and at the radius of maximum velocity, respectively. "Both'' means that the mass was evaluated at the last point where both the approaching and receding sides could be measured. For ESO350-38 we present mass estimates obtained both from the model decomposing the velocity field into two dynamical components (DVF) and for the "raw'' velocity field. For ESO338-04 some points in the velocity field had to be masked in order to at all be able to derive a rotation curve. NB: for all entries, the quoted uncertainties represent the maximum expected deviation, i.e. rather 3-sigma than 1-sigma deviations.

**Table 4:** Derived global properties.
Galaxy	SFR	$M_{\rm ph,26}$	M/L₂₆	$SFR/M_{\rm ph,26}$	$\tau_{\rm ph}$	$\tau_{\rm b}$	$r_{\rm e,d}$	$\sigma$	$M_\sigma$
	$M_{\odot }$ /yr	${10^9~M_{\odot}}$		10^-9 yr^-1	Gyr	Myr	kpc	kms^-1	${10^9~M_{\odot}}$
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
ESO 350-IG38	18.5	15.5	0.87	1.19	0.84	34	2.6	81	18.8
ESO 480-IG12	4.1	5.3	0.83	0.77	1.29	60	2.6	51	7.7
ESO 338-IG04	3.2	4.0	0.85	0.80	1.24	53	2.2	43	4.6
ESO 338-IG04B	0.3	3.2	2.53	0.08	12.1	120	1.7	29	1.6
ESO 185-IG13	5.4	7.1	1.21	0.76	1.32	40	2.0	40	3.7
ESO 400-G43	11.3	12.7	1.07	0.89	1.12	45	3.1	49	8.3
ESO 400-G43B	1.3	4.9	1.52	0.27	3.70	110	2.6	34	3.4
Tololo 0341-403E	1.3	0.3	0.98	4.38	0.23	5	1.6	34	2.1
Tololo 0341-403W	0.9	1.0	1.43	0.90	1.11	19	2.2	36	3.3

Description of column contents: (1) Name of galaxy. (2) Star formation rate (SFR) derived from the integrated H $\alpha$ luminosity, uncorrected for internal extinction. (3) Integrated (disk+burst) photometric mass within the $\mu_{V} = 26$ mag/arcsec² isophote. (4) Integrated V-band mass to light ratio within $\mu_{V} = 26$ mag/arcsec². (5) SFR per unit (photometric) mass of the galaxy. (6) Inverse of $SFR/M_{\rm ph,26}$ , giving the time-scale for building up $M_{\rm ph,26}$ with the current SFR. (7) Time scale for accumulating the observed burst mass with current SFR. (8) Effective (half-light) radius of the disk component. (9) Integrated H $\alpha$ line-width. (10) Mass inferred from the H $\alpha$ line-width.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1027_fig2.ps}\end{figure}$

Figure 2: Comparison of the photometric and dynamical (rotational) masses. The X-axis shows the logarithm (base 10) of the derived photometric mass in units of $M_{\odot }$ . The Y-axis shows the logarithm of the rotational mass. The data-points are taken from Table 3, except for ESO350-38 (filled triangle) and ESO185-13 (filled circle), where $M_{\rm rot}$ is the sum of the rotational masses of the two distinct components in the velocity field (see Paper I). The diagonal dashed line shows the location of galaxies for which the photometric and rotational masses are equal. The arrow in the lower right shows the effect of going from H₀ = 75 to 50 kms^-1/Mpc.

2.6 Photometric mass estimates, and comparison with rotational masses

Photometric masses were derived by integrating the luminosity profiles for the disk and burst components and using their corresponding M/L values. The photometric masses were evaluated at radii taken from characteristics in the rotation curves (e.g. the last measured point or the radius of maximum velocity) to enable comparison with the kinematical mass estimates. In general, the luminosity profiles were integrated out to a radius corresponding to the last point in the rotation curve. In Table 3, we provide the photometric mass estimates, with their lower and upper limits. We also provide the dynamical mass estimate from Paper I, with the lower and upper limits (taking into account the uncertainty in inclination, the intrinsic dispersion, the uncertainty in the parameter f and the difference between different rotation curves or decomposition-models for the individual galaxies). In general, estimating the mass from the rotation curve will underestimate the dynamical mass since most likely these galaxies are not pure rotators. Random motions of the gas could provide significant dynamical support for our BCGs as indicated by their line widths (Table 4). For rotation curves with low amplitude and for the central regions, the contributions from velocity dispersion may dominate over the rotational component (however, see Sect 2.7).

For some galaxies there are several entries in Table 3. This may be the case e.g. when the rotation curve is not monotonously rising, or when there are several dynamical components. In those cases the rotational masses are derived for the relevant radius in question and the photometric mass is given for the same radius. For instance, for ESO350-IG38 we present mass estimates for the last point in the rotation curve, for the maximum rotational velocity and for the two components in the decomposed velocity field (see Paper I). In Fig. 2, the photometric and rotational mass estimates are compared (for reasons of clarity we plot only one point for each galaxy).

In all cases, except for one of the companions, the burst component dominates the optical luminosity (see Table 3). However, the integrated burst mass only makes up 2 to 5% of the total photometric mass. In Table 4, we give $M_{\rm ph,26}$ , the photometric masses integrated out to the $\mu_{V} = 26$ mag/arcsec²isophote. This should be close to the total photometric masses, as the disk component outside these radii should contribute only on the order of one percent of the total mass if the M/L values are similar. In Table 4, we also present M/L₂₆, the global mass to light ratio, derived from $M_{\rm ph,26}$ and the integrated disk+burst light within the corresponding radius.

From Table 3 and Fig. 2 one sees that ESO480-IG12 and ESO338-IG04B are examples in which dark matter is needed within the extent of the rotation curves. In ESO400-IG43B, Tololo0341-403E and Tololo0341-403W the photometric and rotational masses are in good agreement.

ESO350-IG38, ESO338-IG04, ESO185-IG13 and ESO400-IG43 present a deficit in the rotational mass estimates, as compared to the photometric mass. This result can be understood if the systems are not primarily rotationally supported or if the rotation curve does not reflect potential motions, either because the dynamics are not relaxed or if the H $\alpha$ emitting gas is not moving like the stars, even on a large scale. The latter is not so likely although the H $\alpha$ velocities are probably also affected by winds and expanding bubbles. To settle this definitely, the stellar velocity field must be compared with that of the ionised gas. The case of ESO338-IG04 is a clear example of a non-relaxed system in which such a discrepancy between the two mass estimates does exist.

The photometric mass scales with h₇₅^-2, whereas the rotational mass ( $M_{\rm rot}$ ) scales as h₇₅^-1. Hence, the "mass deficiency'' apparent in some galaxies gets worse with lowering of the Hubble constant from the adopted value of 75 kms^-1/Mpc.

2.7 Do the H $\alpha$ line widths trace mass?

Terlevich & Melnick (1981) showed that giant H II-regions display a positive correlation between radius, the H $\beta$ luminosity and the H $\beta$ emission line width. They have argued that this reflects an underlying mass relation and that the H $\beta$ line width traces virial motions. This is somewhat surprising since one expects also other processes, such as SNe feedback, to contribute to the emission line widths. H II galaxies (galaxies with H II region like spectra, i.e. $\sim$ BCGs) seems to follow the same relation, suggesting that they are scaled up versions of giant H II-regions (Melnick et al. 1987). This also makes it possible to use H II galaxies as standard candles to probe cosmological parameters like the H₀ and $\Lambda$ (Melnick et al. 1988, 2000).

$\begin{figure} \par\includegraphics[width=12.6cm,clip]{ms1027_fig3.eps}\end{figure}$

Figure 3: Mass models for ESO350-IG38, ESO480-IG12, ESO338-IG04 and ESO338-IG04B. The filled circles with error bars show the observed rotation curves (see Paper I). The solid line is the photometric rotation curve for the disk component; and the shaded area is the allowed range based on the uncertainty in M/L. The dash-dot line is the stellar disk component from the mass model and the crosses are the halo component; the total model (disk+halo) is shown by the thick long dashed line (only for those cases where the halo component is non-zero). For ESO350-IG38, the rotation curve resulting from the non-decomposed velocity field is shown as filled circles. The main component of the rotation curve for the decomposed velocity field is shown as open circles, and the secondary counter-rotating component is shown as open squares. The dynamical mass model was fitted to the main component of the decomposed velocity field. For ESO338-IG04, the receding side of the rotation curve is shown as filled circles and the approaching side as filled squares. No disk and halo component are shown since it was impossible to construct a dynamical mass model.

If the Balmer emission line widths indeed reflect virial motions, they may be used to derive the dynamical mass of a galaxy. In Table 4, we provide, $r_{\rm e,d}$ , the effective radii of the disk components and $\sigma_{{\rm H}\alpha}$ , the measured H $\alpha$ line-widths ( $\sigma = FWHM/2.35$ ). The $\sigma_{{\rm H}\alpha}$ values are the average line-widths where each pixel is weighted by its H $\alpha$ intensity. They were derived from the velocity dispersion maps rather than from the integrated profiles. Hence the line widths given in Table 4 are not influenced by the overall rotation of the galaxies. The mass which can be supported by velocity dispersion, $M_\sigma$ , was estimated from $M_\sigma = 3 \cdot 1.6 \cdot r_{\rm e,d} \cdot \sigma^2 / G$ , (Guzmán et al. 1996; Bender et al. 1992). With $M_\sigma$ in $M_{\odot }$ , $r_{\rm e,d}$ in kpc, and $\sigma$ in kms^-1, this becomes:

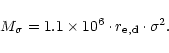
The interesting point is that, for the galaxies which present a deficit in the rotational mass estimate, we can solve the mass discrepancy by invoking that these systems are suported by velocity dispersion instead of rotation. This can be seen by comparing $M_\sigma$ and $M_{\rm ph,26}$ in Table 4. However, this does not solve the problem of why some of our galaxies have such strangely shaped rotation curves, e.g. rapidly declining, as for ESO350-IG38 and ESO400-G43. In general, the mass discrepancies occur outside the centre, which dominates the measured line widths. The ultimate test of the importance of the underlying gravitational potential on the H $\alpha$ line widths would be to derive the stellar velocity dispersion. Kobulnicky & Gebhardt (2000) showed that the central velocity dispersion derived from stars and ionised gas in general agree in a sample of late type galaxies.