The variability of Nd III and Pr III spectral features can be conveniently quantified by considering
time variations of a few low-order moments of a line profile. This observational material can then be used
to identify frequencies and modes of non-radial stellar oscillations. The moment technique was first developed
by Balona (1986a, 1986b), then Aerts et al. (1992) extended and applied this method
to line profile variations of the monoperiodic ![]() Cep star
Cep star ![]() Ceti. The moment method turned out to
be the best mode identification technique for non-degenerate slowly rotating pulsators, and therefore it seems
especially suitable for roAp stars.
Ceti. The moment method turned out to
be the best mode identification technique for non-degenerate slowly rotating pulsators, and therefore it seems
especially suitable for roAp stars.
To measure the first four moments we transformed the wavelength scale ![]() into velocity units v relative
to the center-of-mass velocity, which is the zero point of the variation of the first moment. Then the nth order moment
was computed as
into velocity units v relative
to the center-of-mass velocity, which is the zero point of the variation of the first moment. Then the nth order moment
was computed as
Formal errors of the moment measurements were derived by applying the error propagation laws to formula (5):
![\begin{displaymath}\sigma^2\langle V^n \rangle^j =\sum\limits_i \left [ \frac{\s...
..._i)}{\sum_k y^j_k} (v^n_i - \langle V^n \rangle^j) \right ]^2,
\end{displaymath}](/articles/aa/full/2001/29/aah2579/img63.gif) |
(6) |
Figure 4 illustrates the variations of the line profile moments of doubly ionized REE lines.
Similar to the analysis of the centroid RV variations (Sect. 4), we used non-linear
least-squares sinusoid fitting to find the amplitudes, phases and
constant terms of the moment variations. Time-series of each moment were fitted with
| Amplitude | Nd III 6145.07 Å | Pr III 6160.24 Å | ||||
| zeroth moment: |
||||||
| K0 | 1.90 | 0.16 | 0.89 | 0.22 | ||
| 0.342 | 0.013 | 0.253 | 0.039 | |||
| first moment:
|
||||||
| K1 | 0.452 | 0.022 | 0.784 | 0.028 | ||
| 0.187 | 0.007 | 0.143 | 0.006 | |||
| A1,1 | 0.452 | 0.020 | 0.784 | 0.024 | ||
| second moment:
|
||||||
| K2 | 3.36 | 0.19 | 2.99 | 0.22 | ||
| 0.416 | 0.009 | 0.377 | 0.011 | |||
| A2,0 | 47.59 | 0.15 | 30.12 | 0.16 | ||
| A2,1 | 3.03 | 0.22 | 2.63 | 0.24 | ||
| A2,2 | 0.52 | 0.23 | 0.30 | 0.24 | ||
| third moment:
|
||||||
| K3 | 71.49 | 4.70 | 86.76 | 2.95 | ||
| 0.197 | 0.009 | 0.146 | 0.006 | |||
| A3,1 | 71.15 | 4.70 | 86.11 | 2.91 | ||
| A3,2 | 13.15 | 4.53 | 1.77 | 3.12 | ||
| A3,3 | 0.22 | 4.41 | 6.33 | 2.94 | ||
From the theoretical expressions for the variation of the moments of line profiles of non-radially oscillating
stars (Aerts et al. 1992) we expect the oscillation frequencies 2/P and 3/P to be present in the
variation of the second and third moments. For ![]() Equ the rotation frequency
Equ the rotation frequency ![]() is negligible in comparison
with the pulsation frequency
is negligible in comparison
with the pulsation frequency ![]() .
In this case the expressions of Aerts et al. (1992) for the variation
of the first three moments of a monoperiodic pulsation are given by:
.
In this case the expressions of Aerts et al. (1992) for the variation
of the first three moments of a monoperiodic pulsation are given by:
With the exception of Nd III 6145.07 Å and Pr III 6160.24 Å there are no other lines in the 6140-6166 Å spectral region that are suitable for accurate moment measurements. The other REE lines are weak and blended, while relatively unblended strong lines of lighter elements (Ba II 6141.71 Å, Fe II 6147.74 Å, Ca I 6162.17 Å, and Ca I 6163.76 Å) do not exhibit profile changes. Equivalent width variations at the level above 2 mÅ are also absent for these spectral lines.
During an oscillation cycle the flux at every pixel of the line profile varies with the same period(s). Therefore one can apply
the usual time-series analysis to the variations of the fluxes in individual pixels. In particular,
Fourier frequency analysis with the CLEAN algorithm (e.g. De Mey et al. 1998) helps to extract periodicities present in
the pulsation spectrum. For moderately and rapidly rotating non-radial pulsators such line profile analysis is also the
only way to detect pulsation modes with high ![]() numbers, since these modes cancel out in disk-averaged
observables such as centroid RV or brightness.
numbers, since these modes cancel out in disk-averaged
observables such as centroid RV or brightness.
Limited time-series of profile variations (similar to out ![]() Equ data) are not well suited for the period determination, but
can be efficiently analysed with the least-squares algorithm described by Mantegazza (2000).
In this method variation of the ith pixel is approximated by the
superposition of n sinusoidal components, corresponding to n detected frequencies
Equ data) are not well suited for the period determination, but
can be efficiently analysed with the least-squares algorithm described by Mantegazza (2000).
In this method variation of the ith pixel is approximated by the
superposition of n sinusoidal components, corresponding to n detected frequencies
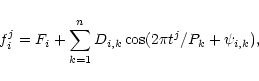 |
(9) |
In the analysis of line profile variations of Nd III 6145.07 Å and Pr III 6160.24 Å
we assumed that variations with a single period (P2 for Nd III and P1 for Pr III) are present and derived the estimate
of the average line profile
![]() together with the variation of the pulsation amplitude
together with the variation of the pulsation amplitude
![]() and phase
and phase
![]() across the line profiles. Figure 5 shows these functions and their formal errors.
across the line profiles. Figure 5 shows these functions and their formal errors.
Unfortunately elaborate modelling techniques developed in recent years for the spectroscopic analysis of non-radial oscillations
of normal stars are not directly applicable and cannot be easily adapted for roAp pulsations.
In most of the studies of line profile variations in non-radially pulsating stars
the pulsation axis is assumed to be aligned with the rotation axis. Therefore an inclination angle is one of the important
parameters. In roAp stars a general model describing stellar pulsations is the oblique pulsator model (Kurtz 1982).
According to this model the pulsation axis is aligned with the magnetic rather than the rotation axis. Hence, we have to use an
inclination of the magnetic axis to the line of sight (angle ![]() )
instead of the usual inclination angle. As the star
rotates the angle
)
instead of the usual inclination angle. As the star
rotates the angle ![]() varies and therefore the pulsation amplitudes are modulated with rotation period. This effect has to be
properly taken into account in the analysis of rapidly rotating roAp stars, but with the extremely slow rotation of
varies and therefore the pulsation amplitudes are modulated with rotation period. This effect has to be
properly taken into account in the analysis of rapidly rotating roAp stars, but with the extremely slow rotation of ![]() Equ
we do not expect to see any rotational modulation of the pulsations and can treat the star as if it were
a
Equ
we do not expect to see any rotational modulation of the pulsations and can treat the star as if it were
a ![]() Scuti-type variable observed at inclination angle
Scuti-type variable observed at inclination angle ![]() .
Besides variable orientation of the pulsation
axis, a strong magnetic field, which is present in the atmospheres of many roAp stars, alters the pulsation velocity field
(e.g. Bigot et al. 2000) and simultaneously introduces Zeeman broadening and splitting of spectral lines. The
latter effect makes a Gaussian approximation of the local line profile (Aerts et al. 1992; Schrijvers et al. 1997)
highly questionable. Despite all these ambiguities, in this section we
try to identify the pulsation mode of
.
Besides variable orientation of the pulsation
axis, a strong magnetic field, which is present in the atmospheres of many roAp stars, alters the pulsation velocity field
(e.g. Bigot et al. 2000) and simultaneously introduces Zeeman broadening and splitting of spectral lines. The
latter effect makes a Gaussian approximation of the local line profile (Aerts et al. 1992; Schrijvers et al. 1997)
highly questionable. Despite all these ambiguities, in this section we
try to identify the pulsation mode of ![]() Equ
applying methods developed for normal non-radial pulsators to the
variation of Pr III and Nd III spectral lines. This semi-qualitative analysis
should be regarded with caution and it by no means aspires to reach any definite conclusions about the pulsation velocity
distribution in the atmosphere of
Equ
applying methods developed for normal non-radial pulsators to the
variation of Pr III and Nd III spectral lines. This semi-qualitative analysis
should be regarded with caution and it by no means aspires to reach any definite conclusions about the pulsation velocity
distribution in the atmosphere of ![]() Equ.
Equ.
In principle diagrams that show the behaviour of the phases of each mode across the line profiles (Fig. 5) are able to
discriminate between pulsation modes with different ![]() and m.
Telting & Schrijvers (1997) determined linear relations between the observed phase difference and mode parameters
and m.
Telting & Schrijvers (1997) determined linear relations between the observed phase difference and mode parameters
![]() and |m| for non-radially pulsating rotating stars. It is not correct to apply directly these relations
for
and |m| for non-radially pulsating rotating stars. It is not correct to apply directly these relations
for ![]() Equ because they were obtained for a rapidly rotating star,
which is not fulfilled in our case.
However we expect to get a lower limit for
Equ because they were obtained for a rapidly rotating star,
which is not fulfilled in our case.
However we expect to get a lower limit for ![]() using the proposed method.
From Telting & Schrijvers' Eq. (9) we get
using the proposed method.
From Telting & Schrijvers' Eq. (9) we get
![]() ,
where
,
where
![]() is the blue-to-red phase difference for the variations with the main pulsation frequency (middle panels in
Fig. 5). For both
Pr III and Nd III lines
is the blue-to-red phase difference for the variations with the main pulsation frequency (middle panels in
Fig. 5). For both
Pr III and Nd III lines
![]() or 1.67
or 1.67![]() ,
therefore
,
therefore
![]() .
.
A consideration of the shape of the amplitude and phase diagrams for individual spectral lines opens another possibility
for mode identification. In particular, the similarity of our pixel-by-pixel
amplitude and phase diagrams to those derived for 5.31 d-1 mode of
![]() Scuti-type variable HD 2724 (Mantegazza & Poretti 1998), for which
Scuti-type variable HD 2724 (Mantegazza & Poretti 1998), for which
![]() and
and ![]() was obtained, allows us to propose
was obtained, allows us to propose
![]() and
and
![]() for the mode identification of the
for the mode identification of the ![]() Equ RV pulsations.
The sign of m depends on the angle
Equ RV pulsations.
The sign of m depends on the angle ![]() between line of sight and pulsation (magnetic) axis. This angle
can be determined from the parameters of the
between line of sight and pulsation (magnetic) axis. This angle
can be determined from the parameters of the ![]() Equ magnetic model suggested by Leroy et al. (1994). They found that
published longitudinal and broadband linear polarisation magnetic observations can be fitted with a
dipolar field
Bd = 5.5 kG and two combinations of inclination angle i and angle
Equ magnetic model suggested by Leroy et al. (1994). They found that
published longitudinal and broadband linear polarisation magnetic observations can be fitted with a
dipolar field
Bd = 5.5 kG and two combinations of inclination angle i and angle
![]() between the magnetic and rotation axes (
between the magnetic and rotation axes (
![]() ,
,
![]()
![]() and
and
![]() ,
,
![]()
![]() ). These
two models yield the same
). These
two models yield the same ![]() :
:
| (10) |
An alternative possibility of mode identification comes from moment analysis through the
comparison between the observed moment amplitudes and calculations for a set of parameters
![]() ,
vp and variance
,
vp and variance ![]() of the intrinsic Gaussian stellar profile
(Aerts et al. 1992; Aerts 1996). The most probable combination of (
of the intrinsic Gaussian stellar profile
(Aerts et al. 1992; Aerts 1996). The most probable combination of (
![]() ,
vp)
can be defined as the one for which the weighted squared differencies between observed and calculated moment amplitudes,
,
vp)
can be defined as the one for which the weighted squared differencies between observed and calculated moment amplitudes,
| Nd III 6145.07 Å | Pr III 6160.24 Å | ||||||
| |m| | vp | vp | |||||
| 3 | 3 | 5-6 | 8-14 | 130-160 | 4 | 7-8 | 120-130 |
| 2 | 2 | 6 | 10-11 | 160 | 3-5 | 5-14 | 140-160 |
| 3 | 2 | 6 | 7 | 100-160 | 3-4 | 7-9 | 110-150 |
Copyright ESO 2001