

Up: Time-resolved spectroscopy of the
4 Analysis of radial velocity variations
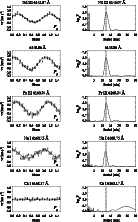 |
Figure 2:
RV curves of selected spectral lines are shown in the left panels. The solid curve is the best-fit
cosine curve. The photometric period which was adopted for this fit is indicated in the lower left corner of each RV panel.
The right panels show periodograms F(P), where F is the probability that the variation with a given period is a
noise artifact. Vertical dotted lines mark the photometric pulsational periods of 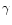 Equ. Equ. |
In the first
step of the analysis of pulsational changes in 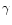 Equ line profiles we computed the difference
between the average and 31 individual spectra and determined a standard deviation for each pixel of the observed
spectral region. Prominent variations of Nd III 6145.07 Å and Pr III 6160.24 Å are immediately
seen in the difference spectra (middle panel in Fig. 1). This is the first clear detection of metal
line profile variability due to the rapid oscillation in a roAp star. Analysis of the standard deviation (lower panel in
Fig. 1) reveals weaker variability in other spectral lines, such as Ba II 6141.71 Å, unidentified
features at 6148.86 and 6150.62 Å, and a complex blend at 6157.8 Å, containing several spectral lines of
REE. The shape of the standard deviation profiles for Nd III and Pr III spectral lines is very similar
to the variability of spectral features in non-radially pulsating
Equ line profiles we computed the difference
between the average and 31 individual spectra and determined a standard deviation for each pixel of the observed
spectral region. Prominent variations of Nd III 6145.07 Å and Pr III 6160.24 Å are immediately
seen in the difference spectra (middle panel in Fig. 1). This is the first clear detection of metal
line profile variability due to the rapid oscillation in a roAp star. Analysis of the standard deviation (lower panel in
Fig. 1) reveals weaker variability in other spectral lines, such as Ba II 6141.71 Å, unidentified
features at 6148.86 and 6150.62 Å, and a complex blend at 6157.8 Å, containing several spectral lines of
REE. The shape of the standard deviation profiles for Nd III and Pr III spectral lines is very similar
to the variability of spectral features in non-radially pulsating 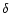 Scuti and
Scuti and 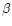 Cep stars
(Mantegazza 2000).
Cep stars
(Mantegazza 2000).
Table 1:
Radial velocity variations of individual spectral lines. Phases 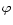 are expressed in units of the period.
Arabic numerals mark the main components of unresolved blends.
are expressed in units of the period.
Arabic numerals mark the main components of unresolved blends.
| Ion |
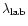 |
K |
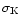 |
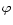 |
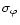 |
P |
| |
Å |
ms-1 |
ms-1 |
|
|
|
| Fe II |
6141.10 |
 120 120 |
|
|
|
|
| Ba II |
6141.71 |
93 |
16 |
0.899 |
0.031 |
2,3 |
| Si I |
6142.48 |
 90 90 |
|
|
|
|
| Ce II |
6143.38 |
296: |
60 |
0.915: |
0.034 |
2,1 |
| Nd III |
6145.071 |
470 |
21 |
0.159 |
0.007 |
2,1 |
| Si I |
6145.021 |
|
|
|
|
|
| La II |
6146.52 |
216: |
49 |
0.944: |
0.039 |
2,3 |
| Cr II |
6147.14 |
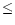 60 60 |
|
|
|
|
| Fe II |
6147.74 |
72: |
16 |
0.674: |
0.037 |
3,4 |
| Pr II |
6148.24 |
348 |
96 |
0.886 |
0.048 |
2 |
| uncl. |
6148.86 |
736 |
30 |
0.060 |
0.006 |
2 |
| Fe II |
6149.26 |
64: |
14 |
0.667: |
0.036 |
3,4 |
| Fe II |
6150.10 |
89: |
35 |
0.473: |
0.073 |
4,3 |
| uncl. |
6150.62 |
557 |
44 |
0.141 |
0.044 |
3,2 |
| Fe I |
6151.62 |
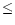 75 75 |
|
|
|
|
| Yb II |
6152.57 |
377: |
95 |
0.881: |
0.045 |
4,3 |
| Na I |
6154.23 |
364 |
72 |
0.893 |
0.032 |
3,4 |
| Si I |
6155.13 |
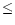 70 70 |
|
|
|
|
| Sm II |
6156.92 |
320 |
50 |
0.953 |
0.025 |
2,3 |
| Fe I |
6157.732 |
209: |
17 |
0.039: |
0.013 |
2,3 |
| Nd II |
6157.822 |
|
|
|
|
|
| Cr II |
6158.113 |
184 |
31 |
0.564 |
0.027 |
1,2 |
| Cr II |
6158.183 |
|
|
|
|
|
| O I |
6158.183 |
|
|
|
|
|
| Ca II |
6158.574 |
137 |
47 |
0.056 |
0.052 |
1,2 |
| Cr II |
6158.624 |
|
|
|
|
|
| Fe I |
6159.385 |
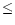 100 100 |
|
|
|
|
| Cr I |
6159.485 |
|
|
|
|
|
| Pr III |
6160.24 |
788 |
37 |
0.169 |
0.007 |
1,2 |
| Na I |
6160.75 |
320 |
30 |
0.958 |
0.016 |
3,4 |
| Pr II |
6161.186 |
339 |
33 |
0.151 |
0.016 |
1,2 |
| Pr III |
6161.226 |
|
|
|
|
|
| Ca I |
6161.306 |
|
|
|
|
|
| Ca I |
6162.17 |
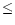 30 30 |
|
|
|
|
| Ca I |
6163.76 |
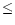 35 35 |
|
|
|
|
| Sm II |
6164.537 |
446 |
56 |
0.926 |
0.022 |
1,2 |
| Ce II |
6164.417 |
|
|
|
|
|
| Fe I |
6165.36 |
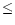 50 50 |
|
|
|
|
We took a closer look at the variability of 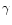 Equ spectral lines by measuring the radial velocity shifts of each
individual spectral feature. The positions of the spectral lines were determined with the help of the center-of-gravity method:
Equ spectral lines by measuring the radial velocity shifts of each
individual spectral feature. The positions of the spectral lines were determined with the help of the center-of-gravity method:
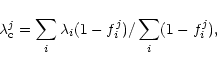 |
(1) |
where fji is the residual flux in the ith pixel of the normalized spectrum and the index j refers to the temporal
sequence of our observations (
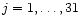 ). Then the wavelength shifts were transformed to the RV scale relative to the
average centroid wavelength
). Then the wavelength shifts were transformed to the RV scale relative to the
average centroid wavelength
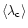
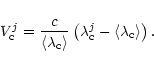 |
(2) |
RV determined in this way proved to be stable and accurate characteristic of spectral line position. An alternative method,
such as fitting analytical profiles to the lines in the observed spectra, is not applicable for the analysis of the complex
profiles of spectral lines altered by magnetic broadening or splitting. On the other hand, measuring RV shifts by cross-correlation
with the average spectrum reduces to the problem of finding the maximum or center-of-gravity of the cross-correlation function and
therefore is equivalent to the direct analysis of individual spectral lines. Besides, centroid RV has the advantage
of being a special case of a more general moment technique (see Sect. 5.1), which proved to be very useful in the
spectroscopic analysis (in particular mode identification) of non-radially pulsating stars.
For the measurements of line positions we usually selected the unblended part of the profiles. RV shifts of a few weak lines
(Fe II 6141.10 Å and Na I 6160.75 Å), situated in the wings of strong spectral features, were also
determined. The resolved Zeeman components of Fe II 6149.26 Å were analysed separately and the results were averaged,
but for all other
weaker features with partially resolved Zeeman structure (La II 6145.52 Å, Cr II 6147.14 Å, Fe II
6150.10 Å, and Fe I 6151.62 Å) we determined common line centers.
The errors of centroid RV measurements were found from a formal error estimate,
which follows from Eq. (1)
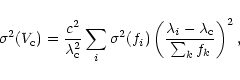 |
(3) |
where the uncertainty
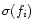 ,
ascribed to the ith pixel of normalized spectrum, is found from the Poisson photon
statistics. In addition, a useful independent estimate of
,
ascribed to the ith pixel of normalized spectrum, is found from the Poisson photon
statistics. In addition, a useful independent estimate of
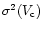 was found by simulating the process of
center-of-gravity measurements. This was done by adding random noise to the average spectrum and determining
was found by simulating the process of
center-of-gravity measurements. This was done by adding random noise to the average spectrum and determining
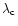 .
The whole procedure was repeated 30-40 times with different noise realisations and the resulting standard deviation
for
.
The whole procedure was repeated 30-40 times with different noise realisations and the resulting standard deviation
for
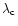 was determined. Both the formal error estimate (3) and Monte-Carlo simulations gave typical
uncertainty of 20-50 ms-1 for RV measurements of strong lines, while errors in the RV determination reach 100-200 ms-1
for weak lines. These error estimates agree well with the standard deviation of individual radial velocity
measurements from the best-fit cosine curves.
was determined. Both the formal error estimate (3) and Monte-Carlo simulations gave typical
uncertainty of 20-50 ms-1 for RV measurements of strong lines, while errors in the RV determination reach 100-200 ms-1
for weak lines. These error estimates agree well with the standard deviation of individual radial velocity
measurements from the best-fit cosine curves.
From the time-series of radial velocity measurements we computed periodograms using the method of Horne & Baliunas
(1986). Since spectroscopic monitoring of 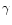 Equ was carried out for only 1.5 hours and we had 31 consecutive
RV measurements for each spectral line, we could not determine the pulsation period with good accuracy and distinguish
pulsation frequencies found in previous photometric studies of
Equ was carried out for only 1.5 hours and we had 31 consecutive
RV measurements for each spectral line, we could not determine the pulsation period with good accuracy and distinguish
pulsation frequencies found in previous photometric studies of 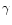 Equ (Martinez et al. 1996). Nevertheless,
useful information about the probability of variation with a certain frequency was obtained from the periodogram
analysis (right panels in Fig. 2).
Equ (Martinez et al. 1996). Nevertheless,
useful information about the probability of variation with a certain frequency was obtained from the periodogram
analysis (right panels in Fig. 2).
For each line we fitted RV variations with a combination of a linear term (to account for spectrograph
drift and Earth motion) and a cosine curve
![\begin{displaymath}V_{\mathrm c}^j = V_0 + V_1 t^j + K \cos[2 \pi (t^j/P+\varphi)],
\end{displaymath}](/articles/aa/full/2001/29/aah2579/img54.gif) |
(4) |
where K is the semi-amplitude of RV variations, 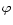 is the phase shift, tj is the time interval between the first and
the jth exposure, V0 and V1 are constants, and P is the adopted period of pulsations. The constant V1 was determined in
the reduction procedure (Sect. 2) and was fixed at
is the phase shift, tj is the time interval between the first and
the jth exposure, V0 and V1 are constants, and P is the adopted period of pulsations. The constant V1 was determined in
the reduction procedure (Sect. 2) and was fixed at
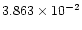 ms-2, while V0, K,
ms-2, while V0, K,
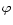 and their errors were found with the help of the non-linear least-squares Marquardt method
(Bevington 1969). A least-squares fit was carried out for each of the pulsation periods determined by
Martinez et al. (1996) (
P1=12.45, P2=12.20, P3=11.93, P4=11.68 min). The results of the analysis of RV variations
are summarised in Table 1. For each spectral line or unresolved blend we give
the identification, laboratory
wavelength, semi-amplitude and phase of RV variation, as well as the corresponding error estimates.
Although our observational data did not allow us to distinguish photometric pulsation frequencies on the basis of
periodogram analysis, we found that fitting RV curves with different photometric periods resulted in different
and their errors were found with the help of the non-linear least-squares Marquardt method
(Bevington 1969). A least-squares fit was carried out for each of the pulsation periods determined by
Martinez et al. (1996) (
P1=12.45, P2=12.20, P3=11.93, P4=11.68 min). The results of the analysis of RV variations
are summarised in Table 1. For each spectral line or unresolved blend we give
the identification, laboratory
wavelength, semi-amplitude and phase of RV variation, as well as the corresponding error estimates.
Although our observational data did not allow us to distinguish photometric pulsation frequencies on the basis of
periodogram analysis, we found that fitting RV curves with different photometric periods resulted in different
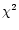 of the fit. In particular, for lines with well defined RV curves the fit with the best out of four
photometric periods resulted in a
of the fit. In particular, for lines with well defined RV curves the fit with the best out of four
photometric periods resulted in a 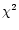 which was a factor of 2-3 smaller than the value derived by adopting
the worst period. Thus, we felt it useful to indicate in the last
column of Table 1 the photometric period that corresponds to the lowest
which was a factor of 2-3 smaller than the value derived by adopting
the worst period. Thus, we felt it useful to indicate in the last
column of Table 1 the photometric period that corresponds to the lowest 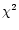 of the fit. If
of the fit. If 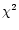 of the two best-fit periods did not differ by more than 30%, we listed both periods in order of increasing
of the two best-fit periods did not differ by more than 30%, we listed both periods in order of increasing
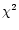 .
For some spectral lines only upper limits of K could be determined, while for other spectral features Kand
.
For some spectral lines only upper limits of K could be determined, while for other spectral features Kand 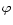 strongly depend on the selection of the part of the line profile used for RV measurements, hence we marked
these results as uncertain. Figure 3 displays the amplitudes and phases of RV curves for variable spectral lines.
strongly depend on the selection of the part of the line profile used for RV measurements, hence we marked
these results as uncertain. Figure 3 displays the amplitudes and phases of RV curves for variable spectral lines.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2579f3.eps}\end{figure}](/articles/aa/full/2001/29/aah2579/Timg56.gif) |
Figure 3:
Amplitude and phases of the RV variations of spectral lines and blends dominated by doubly ionized REE
(filled triangles), singly
ionized REE (open circles), Na I (filled squares), Ba II (asterisk) and
iron-peak elements (open squares). Unidentified spectral lines
are marked by filled circle (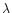 6148.86 Å) and open triangle (
6148.86 Å) and open triangle (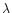 6150.62 Å).
6150.62 Å). |
Figure 2 shows examples of RV curves and periodograms, computed for Nd III 6145.07 Å, an unidentified feature
at 6148.86 Å, Pr III 6160.24 Å, Na I 6160.75 Å, and Ca I 6162.17 Å. Savanov et al. (1999)
already mentioned that the 6148.86 Å line shows high amplitude RV variations, and they proposed it belongs to the second ions of REE
from the similarity of the RV amplitudes. Our detailed analysis of both RV amplitudes and phase shifts shows that the line may
belong either to singly or to doubly ionized REE.
For the two strongest lines of doubly ionized REE we tried to determine the pulsation period
directly by a non-linear fit of a sinusoid to the RV curve.
We found
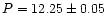 min for Nd III 6145.07 Å and
min for Nd III 6145.07 Å and
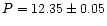 min for Pr III 6160.24 Å, while pulsational amplitudes and phase shifts did not change significantly
in comparison with the values given in Table 1.
min for Pr III 6160.24 Å, while pulsational amplitudes and phase shifts did not change significantly
in comparison with the values given in Table 1.
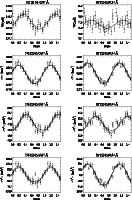 |
Figure 4:
Variation of the equivalent width and first three moments of Nd III 6145.07 Å and Pr III 6160.24 Å spectral lines.
Thick line shows
the fit by a cosine curve (7), while thin line on
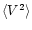 and
and
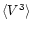 panels
illustrate the fit with formula (8).
panels
illustrate the fit with formula (8). |


Up: Time-resolved spectroscopy of the
Copyright ESO 2001
![]() Equ line profiles we computed the difference
between the average and 31 individual spectra and determined a standard deviation for each pixel of the observed
spectral region. Prominent variations of Nd III 6145.07 Å and Pr III 6160.24 Å are immediately
seen in the difference spectra (middle panel in Fig. 1). This is the first clear detection of metal
line profile variability due to the rapid oscillation in a roAp star. Analysis of the standard deviation (lower panel in
Fig. 1) reveals weaker variability in other spectral lines, such as Ba II 6141.71 Å, unidentified
features at 6148.86 and 6150.62 Å, and a complex blend at 6157.8 Å, containing several spectral lines of
REE. The shape of the standard deviation profiles for Nd III and Pr III spectral lines is very similar
to the variability of spectral features in non-radially pulsating
Equ line profiles we computed the difference
between the average and 31 individual spectra and determined a standard deviation for each pixel of the observed
spectral region. Prominent variations of Nd III 6145.07 Å and Pr III 6160.24 Å are immediately
seen in the difference spectra (middle panel in Fig. 1). This is the first clear detection of metal
line profile variability due to the rapid oscillation in a roAp star. Analysis of the standard deviation (lower panel in
Fig. 1) reveals weaker variability in other spectral lines, such as Ba II 6141.71 Å, unidentified
features at 6148.86 and 6150.62 Å, and a complex blend at 6157.8 Å, containing several spectral lines of
REE. The shape of the standard deviation profiles for Nd III and Pr III spectral lines is very similar
to the variability of spectral features in non-radially pulsating ![]() Scuti and
Scuti and ![]() Cep stars
(Mantegazza 2000).
Cep stars
(Mantegazza 2000).
![]() Equ spectral lines by measuring the radial velocity shifts of each
individual spectral feature. The positions of the spectral lines were determined with the help of the center-of-gravity method:
Equ spectral lines by measuring the radial velocity shifts of each
individual spectral feature. The positions of the spectral lines were determined with the help of the center-of-gravity method:
![]() Equ was carried out for only 1.5 hours and we had 31 consecutive
RV measurements for each spectral line, we could not determine the pulsation period with good accuracy and distinguish
pulsation frequencies found in previous photometric studies of
Equ was carried out for only 1.5 hours and we had 31 consecutive
RV measurements for each spectral line, we could not determine the pulsation period with good accuracy and distinguish
pulsation frequencies found in previous photometric studies of ![]() Equ (Martinez et al. 1996). Nevertheless,
useful information about the probability of variation with a certain frequency was obtained from the periodogram
analysis (right panels in Fig. 2).
Equ (Martinez et al. 1996). Nevertheless,
useful information about the probability of variation with a certain frequency was obtained from the periodogram
analysis (right panels in Fig. 2).
![\begin{displaymath}V_{\mathrm c}^j = V_0 + V_1 t^j + K \cos[2 \pi (t^j/P+\varphi)],
\end{displaymath}](/articles/aa/full/2001/29/aah2579/img54.gif)
![]() min for Nd III 6145.07 Å and
min for Nd III 6145.07 Å and
![]() min for Pr III 6160.24 Å, while pulsational amplitudes and phase shifts did not change significantly
in comparison with the values given in Table 1.
min for Pr III 6160.24 Å, while pulsational amplitudes and phase shifts did not change significantly
in comparison with the values given in Table 1.
