In calculation of the tilt angle, the magnetic flux-weighted center is determined as the position
of each magnetic polarity. This position could be approximately indicated by the magnetic flux
weighted center of each magnetic polarity in the line-of-sight as:
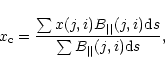
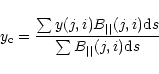
We determinate the sign of the tilt angle of the magnetic polarity axis in an active
region magnetic field such that: in the northern hemisphere, if the S polarity is closer to
the solar equator, the tilt of the active region is positive (
![]() degree), otherwise
the tilt is negative (
degree), otherwise
the tilt is negative (
![]() degree); in the southern hemisphere, the tilt
is negative (
degree); in the southern hemisphere, the tilt
is negative (
![]() degree) when the N polarity is closer to the equator,
and otherwise the tilt is positive (
degree) when the N polarity is closer to the equator,
and otherwise the tilt is positive (
![]() degree). Note that in the 22nd solar cycle,
the leading spot
should be S/N-polarity in the northern/southern hemisphere. Thus, active regions with
a tilt angle
degree). Note that in the 22nd solar cycle,
the leading spot
should be S/N-polarity in the northern/southern hemisphere. Thus, active regions with
a tilt angle
![]() degree in the northern hemisphere, or
degree in the northern hemisphere, or
![]() degree in the southern hemisphere, all adhere to Joy's Law.
Figure 1 shows the sign convention of the tilt angles (
degree in the southern hemisphere, all adhere to Joy's Law.
Figure 1 shows the sign convention of the tilt angles (![]() )
in the 22nd solar cycle.
)
in the 22nd solar cycle.
Current helicity plays an important role in the study of twisted magnetic
fields in the solar atmosphere. Its density can be split into two parts,
| = | |||
| = | |||
| = | (3) |
In the approximation of the force-free magnetic field:
![]() ,
there is,
,
there is,
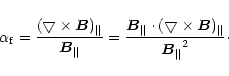 |
(4) |
| = | |||
| = | 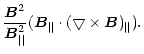 |
(5) |
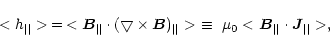 |
(6) |
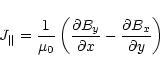
In order to minimize the effect of observational error, the current helicity h|| is
calculated only in pixels as
B|| > 20 G,
![]() G and current density
J||> 0.001 Am-2, with the noise level of
J||(j,i). Eventually, Bao et al. (1998)
determined an average of the current helicity for each active region.
In this case, the uncertainty of magnetic fields affects <h||> very little.
We evaluated the error in 2
G and current density
J||> 0.001 Am-2, with the noise level of
J||(j,i). Eventually, Bao et al. (1998)
determined an average of the current helicity for each active region.
In this case, the uncertainty of magnetic fields affects <h||> very little.
We evaluated the error in 2![]() in Figs. 2 and 3. However,
although an active region develops over days, the sign of < h||>and the sign of the tilt angle of the active region
do not change.
in Figs. 2 and 3. However,
although an active region develops over days, the sign of < h||>and the sign of the tilt angle of the active region
do not change.
Copyright ESO 2001