We use the data of vector magnetic fields obtained by the Solar Magnetic Field Telescope,
an imaging vector magnetograph installed at Huairou Solar Observing Station of the Beijing
Astronomical Observatory, with a field of view of about 5
![]()
![]()
![]() 63
(
63
(
![]() pixels
of the CCD). The temporal and spatial resolution of the vector magnetograms depend on
the number of video frames that are integrated to make one magnetogram. Each
magnetogram used in this paper is the sum of 256 individual frames for both line-of-sight and
transverse fields. Temporal resolution is about 5 min for each vector magnetogram.
Each pixel is about 0
pixels
of the CCD). The temporal and spatial resolution of the vector magnetograms depend on
the number of video frames that are integrated to make one magnetogram. Each
magnetogram used in this paper is the sum of 256 individual frames for both line-of-sight and
transverse fields. Temporal resolution is about 5 min for each vector magnetogram.
Each pixel is about 0
![]()
![]()
![]() 4.
After performing a
4.
After performing a ![]() pixels smoothing average,
the spatial
resolution is 2
pixels smoothing average,
the spatial
resolution is 2
![]() 2
2
![]() .
.
The vector magnetic field in the photosphere was obtained on the basis of narrow-band
images (filtergrams) of four Stokes parameters I, V, Q, U in FeI 5324.191 Å. The
longitudinal magnetic field strength (B||) and transverse magnetic field strength (![]() )
are given, respectively, by
)
are given, respectively, by
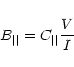 |
(1) |
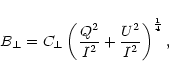 |
(2) |
The 180-degree azimuthal ambiguity in determining the transverse field direction is
an intrinsic defect of the Zeeman effect (Harvey 1969). It may be resolved according to the
potential field approximation method (Wang & Lin 1993; Wang et al. 1994) taking
into account the evolution of active regions and the orientation of chromospheric fibrils.
After the 3![]() 4 pixel smoothing average of V, Q and U was made, the noise level
was less than 10 G for the line-of-sight field and 100 G for the transverse field over the same
integration time.
4 pixel smoothing average of V, Q and U was made, the noise level
was less than 10 G for the line-of-sight field and 100 G for the transverse field over the same
integration time.
It should be mentioned that magneto-optical effects (Faraday rotation) is insignificant
(Wang et al. 1996) in FeI 5324.191 Å. Several tests were made particularly to compare
the measured field azimuth for a few sunspots when switching the bandpass from line
center to line wing, and differences in the observed azimuth were less than 10![]() .
On the
other hand, after Bao et al. (2000) compared the vector magnetograms of an active
region, NOAA 5747, from Huairou and Mees Solar Observation, they found a qualitative
agreement between them. Then, they estimated that Faraday rotation in the Huairou
magnetogram contributes about 12
.
On the
other hand, after Bao et al. (2000) compared the vector magnetograms of an active
region, NOAA 5747, from Huairou and Mees Solar Observation, they found a qualitative
agreement between them. Then, they estimated that Faraday rotation in the Huairou
magnetogram contributes about 12![]() in the azimuth difference when possible sources of error
are taken into account. After considering the role of Faraday rotation in computation of
< h|| >, Bao et al. (2000) conclude that it does not affect the strength of the hemispheric
helicity rule.
in the azimuth difference when possible sources of error
are taken into account. After considering the role of Faraday rotation in computation of
< h|| >, Bao et al. (2000) conclude that it does not affect the strength of the hemispheric
helicity rule.
In our study, we have chosen 286 active regions which belong to ![]() sunspots in the
magnetic classification. Most of the active regions are formed by two main bigger spots.
Among them, 203 active regions have simpler magnetic configuration (i.e. the magnetic
fields in these regions can be simply divided into areas with N and S polarities) and 83
are more complicated (i.e. there is some small scale inverse regions in
the dominated polarities).
sunspots in the
magnetic classification. Most of the active regions are formed by two main bigger spots.
Among them, 203 active regions have simpler magnetic configuration (i.e. the magnetic
fields in these regions can be simply divided into areas with N and S polarities) and 83
are more complicated (i.e. there is some small scale inverse regions in
the dominated polarities).
We analyze the vector magnetograms of these active regions obtained from 1988 to 1996 at Huairou Solar Observing Station of the Beijing Astronomy Observatory, and compare them with their images of sunspots in the photosphere and fulldisk magnetograms published in the SGD. It is found that these active region are much better bipolar regions and are isolated from others. The magnetograms always cover the entire active region. All the vector magnetic field data included in this study were carefully chosen and acquired with favorable weather and seeing conditions during the observations. Thus, the noise level could be lowered to 6 G for the line-of-sight field and 60 G for the transverse field in the photosphere. When an active region developed maturely and was located near the central meridian, it is included in the sample. Therefore, most of the active regions are not new emerging and young active regions. We then calculate tilts and current helicity of those active regions using the best magnetograms. The projection effect for high latitude active regions were removed according to the formulae given by Gary & Hagyard (1990).
Copyright ESO 2001