

Up: Statistical equilibrium and photospheric Vega
Subsections
4 Non-LTE calculations for Vega
The Vega model atmosphere is the same as used in the non-LTE abundance
analysis of nitrogen (Rentzsch-Holm 1996).
It was generated with the ATLAS9 code (Kurucz 1992), adopting
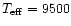 K,
K,
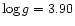 ,
,
![$[{\rm M}/{\rm H}] = -0.5$](/articles/aa/full/2001/27/aa1145/img139.gif) ,
and a depth-independent
microturbulence
,
and a depth-independent
microturbulence 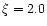 kms-1.
The adopted subsolar metallicity is in accordance with recent non-LTE
analyses (see Rentzsch-Holm 1996), e.g.
kms-1.
The adopted subsolar metallicity is in accordance with recent non-LTE
analyses (see Rentzsch-Holm 1996), e.g.
![$[{\rm C}/{\rm H}] = -0.30 \pm 0.18$](/articles/aa/full/2001/27/aa1145/img141.gif) for carbon
(Stürenburg & Holweger 1991).
The applied model atom is the same as for the Sun.
for carbon
(Stürenburg & Holweger 1991).
The applied model atom is the same as for the Sun.
The resulting departure coefficients of Si I
(Fig. 6) show that low-lying energy levels are
strongly underpopulated with respect to LTE,
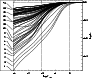 |
Figure 6:
Departure coefficients of Si I in Vega. |
implying substantial
overionisation. Most of the silicon is in the singly ionized stage.
The two lowest energy levels of Si II are almost perfectly in LTE
(Fig. 7) but most of the excited Si II levels are
overpopulated with respect to LTE. The ground state of Si III is also
illustrated in Fig. 7.
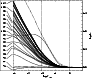 |
Figure 7:
Departure coefficients of Si II in Vega. The dashed line
represents the ground state of Si III. |
Again, strong
overpopulation is obvious. However, the fraction of silicon present as
Si III is still small compared to Si II.
The abundance analysis of Vega is based on low-noise high-resolution
photographic spectra kindly provided by R. Griffin
(Griffin & Griffin 1977) covering the visible spectral region.
Seven Si II lines
(Table 5) were found to be suitable for a reliable
abundance determination,
whereas all Si I lines are much too weak.
Equivalent widths were measured directly from the tracings.
Line broadening is treated in the same way as in the foregoing solar abundance
determination. As for the Sun, the oscillator strengths compiled
by Wiese et al. (1969) and Fuhr & Wiese (1998) produce
a larger abundance scatter (
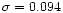 dex) than the values
taken from VALD (
dex) than the values
taken from VALD (
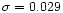 dex).
For this reason the latter set is used. The lines marked with a and c in
Table 5 are close blends of Si II lines.
Consequently, the listed equivalent widths refer to the entire blend,
and these blends are only considered with half weight.
The line marked with b is also weighted half because it is blended
with a Fe I line.
dex).
For this reason the latter set is used. The lines marked with a and c in
Table 5 are close blends of Si II lines.
Consequently, the listed equivalent widths refer to the entire blend,
and these blends are only considered with half weight.
The line marked with b is also weighted half because it is blended
with a Fe I line.
The non-LTE corrections are all negative with values between -0.062and -0.106 with the exception of
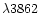 .
For this particular line the non-LTE correction is positive (+0.05)
because the departure coefficient of the upper level exceeds that
of the lower level, contrary to the other lines.
.
For this particular line the non-LTE correction is positive (+0.05)
because the departure coefficient of the upper level exceeds that
of the lower level, contrary to the other lines.
From these 7 lines a weigthed LTE abundance of
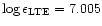 was derived.
The small mean non-LTE correction of
was derived.
The small mean non-LTE correction of
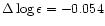 finally leads to a silicon abundance of
finally leads to a silicon abundance of
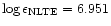 with a standard deviation of
0.029 dex. The estimated error limits, including uncertainties in the
equivalent widths, are
with a standard deviation of
0.029 dex. The estimated error limits, including uncertainties in the
equivalent widths, are  0.1 dex.
Table 6 shows the influence of the line broadening
parameters and the microturbulence on the mean non-LTE abundance compared
to the described standard Vega model.
0.1 dex.
Table 6 shows the influence of the line broadening
parameters and the microturbulence on the mean non-LTE abundance compared
to the described standard Vega model.
For a smaller microturbulence of
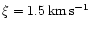 ,
the resulting non-LTE abundances increases by +0.228 dex.
Unlike the Sun, van der Waals broadening is less important than Stark
broadening, as expected for an A star. Completely neglecting the Stark broadening
causes an abundance deviation of +0.119 dex from the standard model.
,
the resulting non-LTE abundances increases by +0.228 dex.
Unlike the Sun, van der Waals broadening is less important than Stark
broadening, as expected for an A star. Completely neglecting the Stark broadening
causes an abundance deviation of +0.119 dex from the standard model.
For comparison, Hill (1995) and Lemke (1990) obtained
values of
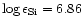 and
and
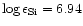 ,
respectively, which is in good agreement with the result of this
work.
,
respectively, which is in good agreement with the result of this
work.
The abundance of silicon in Vega differs by -0.599 dex
from the solar value, confirming the deficiency of Si found by
other authors.


Up: Statistical equilibrium and photospheric Vega
Copyright ESO 2001
![]() K,
K,
![]() ,
,
![]() ,
and a depth-independent
microturbulence
,
and a depth-independent
microturbulence ![]() kms-1.
The adopted subsolar metallicity is in accordance with recent non-LTE
analyses (see Rentzsch-Holm 1996), e.g.
kms-1.
The adopted subsolar metallicity is in accordance with recent non-LTE
analyses (see Rentzsch-Holm 1996), e.g.
![]() for carbon
(Stürenburg & Holweger 1991).
The applied model atom is the same as for the Sun.
for carbon
(Stürenburg & Holweger 1991).
The applied model atom is the same as for the Sun.
