

Up: Statistical equilibrium and photospheric Vega
2 Atomic data
The silicon model atom accounts for the most important levels and
transitions of Si I and Si II and comprises 115 energy
levels and 84 line transitions.
For Si I (ionization limit at 8.15 eV) 75
energy levels up to 7.77 eV and 53 line transitions were
included, for Si II (ionization limit at 16.35 eV) 40 energy
levels up to 15.65 eV and 31 line
transitions were taken into account. The atomic data are listed in
Tables 1 and 2,
while
Fig. 1 shows the corresponding Grotrian diagrams.
The data for the energy levels were adopted from a compilation of
Martin & Zalubas (1983) which is available
from the internet server of the National Institute of Standards and
Technology (NIST, http://physics.nist.gov). This source also
includes some unpublished measurements.
It should be mentioned that apart from LS coupling, other schemes
(
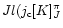 ),
),
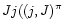 )
were found for Si I.
For consistency and practical reasons the concerned energy levels were
designated to LS coupling if possible (Table 1).
)
were found for Si I.
For consistency and practical reasons the concerned energy levels were
designated to LS coupling if possible (Table 1).
Data for the line transitions used in the model atom
(Table 2) were obtained from the NIST server, the Vienna
Atomic Line Data Base
(Piskunov et al. 1995; Kurucz 1993) and
Lambert & Luck (1978).
The NIST data refer to the compilation of Wiese et al.
(1969) and the newer version by Fuhr & Wiese (1998).
The latter provides improved transition probabilities for some line transitions.
Photoionization cross-sections were taken from the Opacity Project
(Seaton et al. 1992, 1994) for almost all energy
levels with the exception of eleven mostly high excited ones (marked
with * in Table 1).
In these cases the Kramers Gaunt aproximation for hydrogen-like atoms
as given by Allen (1973) was used.
 |
Figure 1:
Grotrian diagrams of the silicon model atom including
Si I with 75 energy levels and 53 line transitions and
Si II with 40 levels and 31 transitions. |
The majority of the more important electron collisional cross-sections
of Si I were calculated using the tables given by Sobelman et al. (1981).
Transistions not covered by the Sobelman tables were treated with the
formulas compiled by Drawin (1967) but additionally needed to
be scaled to the corresponding maximum cross-sections.
For optically allowed transitions, the maximum cross-sections were
calculated with the approximation of Van Regemorter
(1962) using all available oscillator strengths and
additional values from the Opacity Project.
In all other cases, especially for optically forbidden transitions,
the cross-sections were scaled with the collision strength formula
described by Allen (1973).
Drawin (1967) also provides an estimate for collisional
ionization by electrons, which was applied here, and
for inelastic collisions with neutral hydrogen atoms.
Cross-sections for the latter were calculated with the more
generalized formula given by Steenbock & Holweger
(1984).
Due to a complete lack of data, the collisional parameter Q
(maximum cross-section in units of
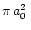 )
in this
formula was set equal to the value of the respective electron collision
(derived via the different approximations for optically allowed and
forbidden bound-bound and bound-free collisions described above) and
was additionally scaled with an empirical factor
)
in this
formula was set equal to the value of the respective electron collision
(derived via the different approximations for optically allowed and
forbidden bound-bound and bound-free collisions described above) and
was additionally scaled with an empirical factor
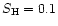 (Holweger
1996).
(Holweger
1996).


Up: Statistical equilibrium and photospheric Vega
Copyright ESO 2001
