A&A 373, 511-535 (2001)
DOI: 10.1051/0004-6361:20010561
Research School of Astronomy and Astrophysics, Australian National University, Mount Stromlo Observatory, Cotter Road, Weston Creek ACT 2611, Australia
Received 2 February 2001 / Accepted 11 April 2001
Abstract
The Galactic bar causes a characteristic splitting of the disc phase space
into regular and chaotic orbit regions which is shown to play an important
role in shaping the stellar velocity distribution in the Solar neighbourhood.
A detailed orbital analysis within an analytical 2D rotating barred potential
reveals that this splitting is mainly dictated by the value of the Hamiltonian
H and the bar induced resonances. In the u-v velocity plane at fixed space
position, the contours of constant H are circles centred on the local solid
rotation velocity of the bar frame and of radius increasing with H. For
reasonable bar strengths, the contour H=H12 corresponding to the
effective potential at the Lagrangian points L1/2 marks the average
transition from regular to chaotic motion, with the majority of orbits being
chaotic at H>H12. On top of this, the resonances generate an alternation
of regular and chaotic orbit arcs opened towards lower angular momentum and
asymmetric in u for space positions away from the principal axes of the bar.
Test particle simulations of exponential discs in the same potential and a
more realistic high-resolution 3D N-body simulation reveal how the
decoupled evolution of the distribution function in the two kind of regions
and the process of chaotic mixing lead to overdensities in the
![]() chaotic part of the disc velocity distributions outside corotation.
In particular, for realistic space positions of the Sun near or slightly
beyond the outer Lindblad resonance and if u is defined positive towards
the anti-centre, the eccentric quasi-periodic orbits trapped around the stable
x1(1) orbits - i.e. the bar-aligned closed orbits which asymptotically
become circular at larger distances - produce a broad
chaotic part of the disc velocity distributions outside corotation.
In particular, for realistic space positions of the Sun near or slightly
beyond the outer Lindblad resonance and if u is defined positive towards
the anti-centre, the eccentric quasi-periodic orbits trapped around the stable
x1(1) orbits - i.e. the bar-aligned closed orbits which asymptotically
become circular at larger distances - produce a broad
![]() regular arc in
velocity space extending within the H>H12 zone, whereas the corresponding
regular arc in
velocity space extending within the H>H12 zone, whereas the corresponding
![]() region appears as an overdensity of chaotic orbits forced to avoid
that arc. This chaotic overdensity
provides an original interpretation, distinct from the anti-bar elongated
quasi-periodic orbit interpretation proposed by Dehnen (2000), for the
prominent stream of high asymmetric drift and predominantly outward moving
stars clearly emerging from the Hipparcos data. However, the most appropriate
interpretation for this stream remains uncertain.
The effects of spiral arms and of molecular clouds are also briefly discussed
within this context.
region appears as an overdensity of chaotic orbits forced to avoid
that arc. This chaotic overdensity
provides an original interpretation, distinct from the anti-bar elongated
quasi-periodic orbit interpretation proposed by Dehnen (2000), for the
prominent stream of high asymmetric drift and predominantly outward moving
stars clearly emerging from the Hipparcos data. However, the most appropriate
interpretation for this stream remains uncertain.
The effects of spiral arms and of molecular clouds are also briefly discussed
within this context.
Key words: Galaxy: kinematics and dynamics - Galaxy: solar neighbourhood - Galaxy: structure - methods: numerical
The kinematics of disc stars in the Solar neighbourhood displays several
long known properties, such as the increase of velocity dispersion with age,
the tendency of young stars to appear in moving groups or streams, and the
classical vertex deviation affecting stars with asymmetric drift down to
![]() 25 kms-1 relative to the Sun and mainly owing to the Hyades and
Sirius streams. Disc heating is traditionally attributed to the diffusion of
stars by transient spiral arms or by massive compact objects like molecular
clouds, the streams to dissolving ensembles of stars born at the same place,
and the vertex deviation to local gravitational perturbations like spiral
arms or local departures from a steady state.
25 kms-1 relative to the Sun and mainly owing to the Hyades and
Sirius streams. Disc heating is traditionally attributed to the diffusion of
stars by transient spiral arms or by massive compact objects like molecular
clouds, the streams to dissolving ensembles of stars born at the same place,
and the vertex deviation to local gravitational perturbations like spiral
arms or local departures from a steady state.
Beside these properties, the local disc velocity distribution also
betrays a broad stream of low angular momentum and mainly outward moving stars
with a mean heliocentric asymmetric drift
![]() kms-1, i.e.
typical of the thick disk (Gilmore et al. 1989), which hereafter will be
referred to as the "Hercules'' stream, according to the comoving Eggen group
kms-1, i.e.
typical of the thick disk (Gilmore et al. 1989), which hereafter will be
referred to as the "Hercules'' stream, according to the comoving Eggen group
![]() Herculis (Skuljan et al. 1999). The mean outward motion of stars
with high asymmetric drift, also known as the "u-anomaly'' and seen up to
over s=100 kms-1 in metal rich samples (Raboud et al. 1998)
and in Mira variables with period between 145 and 200 days (Feast &
Whitelock 2000), is already apparent in early stellar kinematical samples
(Eggen 1966; Woolley et al. 1970) and was recognised long ago by
Mayor (1972), but the clearest evidence for the Hercules stream comes from
the Hipparcos proper motions combined with (Fig. 1) or without (Dehnen
1998) available radial velocities. This stream is very likely to have a
dynamical origin because its stars are older than
Herculis (Skuljan et al. 1999). The mean outward motion of stars
with high asymmetric drift, also known as the "u-anomaly'' and seen up to
over s=100 kms-1 in metal rich samples (Raboud et al. 1998)
and in Mira variables with period between 145 and 200 days (Feast &
Whitelock 2000), is already apparent in early stellar kinematical samples
(Eggen 1966; Woolley et al. 1970) and was recognised long ago by
Mayor (1972), but the clearest evidence for the Hercules stream comes from
the Hipparcos proper motions combined with (Fig. 1) or without (Dehnen
1998) available radial velocities. This stream is very likely to have a
dynamical origin because its stars are older than ![]() 2 Gyr (Caloi et al.
1999) and present a wide range of metallicities (Raboud et al.
1998).
2 Gyr (Caloi et al.
1999) and present a wide range of metallicities (Raboud et al.
1998).
The existence of the Hercules stream is most probably related to the
influence of the Galactic bar. It is now indeed widely accepted that the
Milky Way is a barred galaxy, as are the majority of disc galaxies. Evidence
for the bar comes from longitudinal asymmetry in the bulge surface photometry
(e.g. Blitz & Spergel 1991; Binney et al. 1997), star counts (e.g.
Nakada et al. 1991; Nikolaev & Weinberg 1997; Stanek et al.
1997), interpretation of the observed gas kinematics in the central few
kpc (Binney et al. 1991; Englmaier & Gerhard 1999; Fux
1999; Weiner & Sellwood 1999), large microlensing optical depths
towards the Galactic bulge (Paczynski et al. 1994; Kuijken 1997;
Gyuk 1999; Alcock et al. 2000) and possibly inner stellar
kinematics (Sevenster et al. 1999; see also Gerhard 1999 for a
recent review). Although still not very well constrained, the most quoted
values for the main bar parameters are an in-plane inclination angle with
respect to the Galactic centre direction
![]() ,
with the near side of the bar in the
first Galactic quadrant, and a corotation radius
,
with the near side of the bar in the
first Galactic quadrant, and a corotation radius
![]() kpc.
kpc.
Barred N-body models of the Milky Way produce a mean outward
motion of disc particles at realistic positions of the Sun relative to the bar
(Fux et al. 1995; Raboud et al. 1998), but the precise bar
induced dynamical process leading to the observed kinematical properties of
the Hercules stream is still a matter of debate. Dehnen (1999b, 2000
- hereafter D2000) relates this stream and the main mode of high angular
momentum stars in the observed velocity distribution to the coexistence near
the outer Lindblad resonance (OLR) of two distinct types of periodic orbits
replacing the circular orbit close to the OLR in a rotating barred potential,
i.e. the same idea introduced by Kalnajs (1991) to explain the Hyades and
Sirius streams. Linear theory indeed predicts that the orientation of orbits
closing in the bar rotating frame changes across the main resonances
associated with the bar (Binney & Tremaine 1987). In particular,
periodic orbits outside and inside the OLR radius are respectively elongated
along the major and minor axis of the bar, and both types of orbits, as well
as the quasi-periodic orbits trapped around these orbits, can overlap in space
near the OLR. According to D2000, the Hercules stream and the main velocity
mode, respectively "OLR'' and "LSR'' mode in his terminology, result from
the anti-bar and bar elongated orbits respectively, and the valley between the
two modes from off-scattered stars on unstable OLR orbits. Raboud et al.
(1998), on the other hand, suggest that the Hercules stream involves
stars merely on chaotic orbits and susceptible to cross the corotation radius
and wander throughout the Galaxy, but do not explicitly justify why such stars
should move outwards on the average in the Solar neighbourhood. One motivation
for this interpretation is that of order ![]() of the particles in
N-body models of barred galaxies indeed follow such orbits (e.g.
Pfenniger & Friedli 1991).
of the particles in
N-body models of barred galaxies indeed follow such orbits (e.g.
Pfenniger & Friedli 1991).
This paper investigates how the barred potential of the Milky Way divides the phase space of the stellar disc into regions of regular and chaotic motion and how this segregation may explain some properties of the observed local stellar kinematics and in particular help to clarify the real nature of the Hercules stream. The investigation is first performed in details using the same analytical two-dimensional rotating barred potential as in D2000 and then complemented with the results from a more realistic high-resolution three-dimensional N-body simulation.
The structure of the paper is as follow: Sect. 2 briefly
presents the observed stellar velocity distribution in the Solar neighbourhood
and some further informations about the Hercules stream. Section 3
recalls a dynamical classification of orbits in rotating barred potentials
based on the Jacobi integral and determines the location in local velocity
space of the class of orbits that may cross the corotation radius.
Section 4 describes the analytical barred potential adopted in the 2D
study and Sect. 5 the main periodic orbits supported by this
potential outside corotation. Section 6 derives the associated
regular and chaotic regions in velocity space as a function of space position
relative to the bar. Section 7 presents the velocity
distributions at the same space positions resulting from test particle
simulations and examines the role of chaos in shaping these distributions.
Section 8 shows how the derived velocity distributions depend on
the initial conditions of the simulations and Sect. 9 how the
particles initially on OLR orbits eventually contribute to these distributions.
Section 10 gives the results inferred from the 3D N-body
simulations. Section 11 makes a quantitative comparison of the model
velocity distributions with the observed one and discusses the most likely
origin of the Hercules stream. Finally, Sect. 12 sums up.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS1098f01.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg45.gif) |
Figure 1:
Heliocentric velocity distribution in the u-v plane of all the
Hipparcos single stars with
|
| Open with DEXTER | |
There are several attempts to recover the velocity distribution of stars in the Solar neighbourhood from the Hipparcos data published in the recent literature (e.g. Dehnen 1998 and Skuljan et al. 1999 for all stellar types; Chereul et al. 1998 and Asiain et al. 1999 for early-type stars). The main features of the u-v distribution are illustrated in Fig. 1 and the mean velocities of the highlighted streams are listed in Table 1. Throughout this paper, v and u respectively stand for the azimuthal and radial velocity components, with positive values towards galactic rotation and towards the Galactic anti-centre, and w for the vertical velocity component.
The main sample selected for this figure is built from the 3481 single
stars of the Hipparcos Catalogue with relative errors on parallaxes less than
10%, distances less than 100 pc, and given radial velocities in the
Hipparcos Input Catalogue. Here, an entry of the Hipparcos Catalogue is
considered as a single star if the CCDM identifier and Multiple System Annex
flag (fields H55 and H59 respectively) are void, the number of components
(field H58) is 1 and the solution quality (field H61) is different from "S''.
Two disjoint sub-samples are isolated from this main sample, the first one
restricted to the 1707 stars with B-V>0.6, representing stars which are
older on the average than the stars in the full sample, and the second one
to the 855 stars with B-V<0.4, representing essentially main sequence stars
which are younger than 2 Gyr. The diagrams are derived using the adaptative
kernel method described in Skuljan et al. (1999), with an average
smoothing length h=16 kms-1 for the B-V>0.6 sub-sample, and
h=10 kms-1 for the other samples.
| Stream | ||
| Coma Berenices | -4 | 3 |
| Sirius | 3 | -9 |
| Hyades | -18 | 42 |
| Pleiades | -19 | 13 |
| Hercules | -45 | 35 |
| Arcturus | -110 | 16 |
The reader should be warned that stellar samples built this way are kinematically biased in the sense that radial velocities are predominantly known for high proper-motion stars (Binney et al. 1997; Skuljan et al. 1999). Moreover, the completeness of the Hipparcos Catalogue depends on Galactic latitude, so that the effects of such a bias are even further complicated by the anisotropic local velocity distribution. Nevertheless, the resulting velocity distributions closely resemble the asserted unbiased distributions derived by Dehnen (1998), suggesting that kinematical biases do not severely affect our diagrams.
Figure 1 nicely confirms that the Hercules stream involves merely old disc stars. According to D2000, roughly 15% of the Hipparcos stars with B-V>0.6 belong to this stream, but this is likely an underestimate of the corresponding fraction among local old disc stars because such a colour range is still contaminated by young stars which contribute negligibly to the stream and because the Hipparcos catalogue is biased towards young stars. The average luminosity of stars in this catalogue indeed increases with distance and the catalogue essentially covers the vertical region of the Galactic plane where the fraction of young stars is largest.
| |
Figure 2:
a) Effective potential in the x-y plane of a barred disc
model corresponding to Eq. (5) with F=0.10. The bar is along the
y-axis and the spacing between the contours increases by a factor
1.2 towards lower
|
| Open with DEXTER | |
In a rotating barred potential, the contours of effective potential in
the plane of symmetry z=0 look like a volcano with a sinusoidal crest, the
extrema of which defining the locations of the Lagrangian points L1/2 and
L4/5, corresponding respectively to the saddle points and maxima of
![]() on the major and minor axis of the bar (Fig. 2a).
Two critical values of the Hamiltonian are associated with stars corotating at
these points, namely
on the major and minor axis of the bar (Fig. 2a).
Two critical values of the Hamiltonian are associated with stars corotating at
these points, namely
![]() and
and
![]() .
The first of them can be used to
classify stellar orbits into three dynamical categories (Sparke & Sellwood
1987; Pfenniger & Friedli 1991): the bar orbits and disc
orbits with H<H12, which cannot cross the H12 contour and are
therefore confined inside and outside corotation respectively, and the hot orbits with
.
The first of them can be used to
classify stellar orbits into three dynamical categories (Sparke & Sellwood
1987; Pfenniger & Friedli 1991): the bar orbits and disc
orbits with H<H12, which cannot cross the H12 contour and are
therefore confined inside and outside corotation respectively, and the hot orbits with
![]() ,
which are susceptible to cross the corotation
barrier and explore all space except a small region around L4/5 if
H<H45 (Fig. 2b). Stars with
H12<H<H45 cannot cross the
corotation radius at all azimuth and may therefore more likely be locked
during several orbital periods on either side of corotation.
,
which are susceptible to cross the corotation
barrier and explore all space except a small region around L4/5 if
H<H45 (Fig. 2b). Stars with
H12<H<H45 cannot cross the
corotation radius at all azimuth and may therefore more likely be locked
during several orbital periods on either side of corotation.
In the Solar neighbourhood, located confidently beyond corotation, only
stars from the disc and hot populations are observed. Since these stars share
about the same
![]() if not too far from the Galactic plane, their
H-values depend mainly on the velocities and thus one expects that the two
populations occupy different regions in local velocity space. If v, u and
w are measured with respect to the Galactic centre, Eq. (1)
transforms into:
if not too far from the Galactic plane, their
H-values depend mainly on the velocities and thus one expects that the two
populations occupy different regions in local velocity space. If v, u and
w are measured with respect to the Galactic centre, Eq. (1)
transforms into:
| |
Figure 3:
Contours of constant Hamiltonian in the u-v plane of a realistic 2D
barred model (Eq. (5) with
|
| Open with DEXTER | |
From Eqs. (3) and (4), it also follows that the radius
![]() and the velocity separation
and the velocity separation
![]() increase for
larger galactocentric distances relative to
increase for
larger galactocentric distances relative to
![]() .
In
particular, whatever the strength of the bar, one can always increase the
fraction of the Hercules stream falling in the hot orbit region by reducing
the value of
.
In
particular, whatever the strength of the bar, one can always increase the
fraction of the Hercules stream falling in the hot orbit region by reducing
the value of
![]() .
.
The analytical 2D barred potential adopted for the orbital structure analysis
and the test particle simulations is the same as in D2000:
The next sections present a study of the periodic orbits outside corotation in the adopted rotating barred potential, identify the regular and chaotic regions in phase space associated with this potential, and discuss how stars may populate the available orbits. All orbits in these sections are integrated in double precision using an 8 order Runge-Kutta-Fehlberg algorithm (Fehlberg 1968). Two values of the bar strength will be considered, F=0.10 and F=0.20. The larger value corresponds to a rather strong bar (see Sect. 10 for a quantification with respect to real galaxies), but has the advantage to clearly point out the effect of chaos in the test particle simulations. Some of the key results for the intermediate case F=0.15 are presented in Fux (2001a). For comparison, Dehnen's simulations were done in the range F=0.062-0.116.
Much of the orbital structure in a system can be assessed from the study of
its periodic orbits, which sometimes are considered as the skeleton of the
system. While periodic orbits have been widely investigated in 2D and 3D
within bars, only few papers (Athanassoula et al. 1983; Contopoulos &
Grosbol 1989; Sellwood & Wilkinson 1993) discuss them in discs
surrounding bars.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS1098f04new.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg94.gif) |
Figure 4:
Distinct looped periodic orbits in the axisymmetric
potential
|
| Open with DEXTER | |
A good approach to investigate periodic orbits in a 2D rotating barred
potential is to start with the axisymmetric limit. In this case, the only
orbits which close whatever the value of
![]() are the circular
orbits. All other bound orbits can be thought as a libration motion around
these orbits and look like a rosette which never closes, except for some
exceptional potentials like a point mass with
are the circular
orbits. All other bound orbits can be thought as a libration motion around
these orbits and look like a rosette which never closes, except for some
exceptional potentials like a point mass with
![]() ,
or at
resonances, where the radial and azimuthal frequencies
,
or at
resonances, where the radial and azimuthal frequencies
![]() and
and
![]() satisfy the relation:
satisfy the relation:
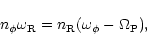 |
(8) |
![\begin{figure}
\par\includegraphics[width=13cm]{MS1098f05new.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg110.gif) |
Figure 5:
a) Characteristic diagram in the rotating axisymmetric
potential (Eq. (6)) for the circular orbit (circ.) and the lowest
order outer
|
| Open with DEXTER | |
The characteristic curves of these resonant orbits in the H-x plane
(Fig. 5a) all intersect the circular orbit curve (COC) at their point
of lowest H, corresponding to a bifurcation. For even resonances, four
branches emanate from the bifurcation, two from the COC and two from the
resonance curve. The resonance branches above (towards larger x) and below
the COC represent orbits with respectively apocentre and pericentre on the
x-axis. The lower branch always passes through the zero velocity
curve (ZVC), where the orbit becomes cuspy on the x-axis and then
develops loops at higher value of the Hamiltonian. For such loop orbits, the
x-coordinate of the characteristic curves does not trace the
pericentre but the place where the orbit self-intersect and
![]() .
For odd resonances, the bifurcation has six branches: the two from the COC,
two for the resonant orbits with radial extrema on the x-axis and
which have properties similar to the former even resonance branches, and two
for the resonant orbits with those extrema on the y-axis. The two
latter branches have opposite
.
For odd resonances, the bifurcation has six branches: the two from the COC,
two for the resonant orbits with radial extrema on the x-axis and
which have properties similar to the former even resonance branches, and two
for the resonant orbits with those extrema on the y-axis. The two
latter branches have opposite ![]() but degenerate into the same curve in
the H-x characteristic diagram. All periodic orbits in the symmetry plane of
an axisymmetric potential are stable.
but degenerate into the same curve in
the H-x characteristic diagram. All periodic orbits in the symmetry plane of
an axisymmetric potential are stable.
Figures 5b and 5c show how the characteristic curves
are modified when the bar component with major axis on the y-axis is
added to the potential. The changes mainly occur at the bifurcations of the
axisymmetric case. The bifurcations of the even resonances become gaps, with
the right (low H) COC branch deviating into the lower resonance branch, and
the upper resonance branch into the left COC branch, giving rise to a sequence
of continuous orbit families. In the terminology introduced by Contopoulos &
Grosbol (1989), the outermost of these families is called x1(1), and
the other families are divided into an upper x1*(i) and a lower x1(i)sub-family at or near the point of minimum H, where the stability of the
orbits appears to reverse. The six-branch bifurcations of the odd resonances
(see the 1/1 and 3/1 resonances in the figures) split into two pitchfork
bifurcations, one involving the resonant orbits symmetric with respect to the
bar minor axis, which are stable near the bifurcation, and the other the
resonant orbits non-symmetric relative to this axis, which are unstable near
the bifurcation and qualified as asymmetric. As a by-product of this
splitting, the segment of the x1(i) characteristic curve between the two
new bifurcations becomes unstable.
![\begin{figure}
\par\includegraphics[width=9.3cm]{MS1098f06new.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg113.gif) |
Figure 6: Orbits of the x1(1) (left) and x1(2) (right) families in the model with bar strength F=0.10, with the thick line representing the orbit of lowest apocentre and of lowest Hamiltonian respectively. The shaded ellipse sketches the bar. The full and dotted lines represent stable and unstable orbits respectively. The nearly circular x1(1) orbits extend out to infinity. Note the unstable x1(1) orbit at the 1/1 resonance. |
| Open with DEXTER | |
At low eccentricity (i.e. small H), only those orbits with a pericentre
on the bar minor axis seem to be stable. This could be the influence of the
Lagrangian points
![]() ,
which are stable fix points in the models. At
high eccentricity, all orbit families undergo a change of stability and the
characteristic curves in Fig. 5 are all interrupted at the point
where the minor axis loop of the orbits touches the centre R=0. The curves
actually go beyond this point, but the resonance number changes. For instance,
the 2/1 orbits become 2/3 orbits. When increasing the bar strength (from
Figs. 5b to 5c), the resonance gaps between successive
x1(i) curves and the separation between the pitchfork bifurcation pairs
increases. The characteristic curves also become more twisted and the fraction
of stable orbits decreases. In particular, almost all x1(3) orbits are
unstable for F=0.20. It should be noted that other authors (Athanassoula et
al. 1983; Sellwood & Wilkinson 1993) report more complicated
characteristic curves for the x1(2) and higher order orbit families near
the ZVC in their models, probably as a consequence of an m=4 Fourier
component in the potential.
,
which are stable fix points in the models. At
high eccentricity, all orbit families undergo a change of stability and the
characteristic curves in Fig. 5 are all interrupted at the point
where the minor axis loop of the orbits touches the centre R=0. The curves
actually go beyond this point, but the resonance number changes. For instance,
the 2/1 orbits become 2/3 orbits. When increasing the bar strength (from
Figs. 5b to 5c), the resonance gaps between successive
x1(i) curves and the separation between the pitchfork bifurcation pairs
increases. The characteristic curves also become more twisted and the fraction
of stable orbits decreases. In particular, almost all x1(3) orbits are
unstable for F=0.20. It should be noted that other authors (Athanassoula et
al. 1983; Sellwood & Wilkinson 1993) report more complicated
characteristic curves for the x1(2) and higher order orbit families near
the ZVC in their models, probably as a consequence of an m=4 Fourier
component in the potential.
Some orbits of the above families are plotted in D2000, but obviously
missing all eccentric x1(1) and x1(2) orbits with loops on the bar minor
axis. A more complete set of orbits from these two families are given in
Fig. 6. These orbits are the most important even ![]() periodic orbits
because they are usually associated with the largest invariant curve islands
in surface of section maps. The orbits drawn with thick lines are examples of
the perpendicularly oriented orbits that replace the circular orbit near the
OLR radius and which have been proposed as a possible explanation for either
the Hyades and Sirius streams (Kalnajs 1991) or the Hercules-LSR
bimodality (D2000) in the observed u-v distribution. As we shall see in the
next sections, the stable eccentric x1(1) orbits also play an important
role in shaping the local velocity distribution. Regular orbits trapped around
them are indeed unlikely to be heavily populated by stars, but represent
forbidden phase space regions for chaotic orbits.
periodic orbits
because they are usually associated with the largest invariant curve islands
in surface of section maps. The orbits drawn with thick lines are examples of
the perpendicularly oriented orbits that replace the circular orbit near the
OLR radius and which have been proposed as a possible explanation for either
the Hyades and Sirius streams (Kalnajs 1991) or the Hercules-LSR
bimodality (D2000) in the observed u-v distribution. As we shall see in the
next sections, the stable eccentric x1(1) orbits also play an important
role in shaping the local velocity distribution. Regular orbits trapped around
them are indeed unlikely to be heavily populated by stars, but represent
forbidden phase space regions for chaotic orbits.
The space coverage of the orbit families can be determined from x-yplots like in Fig. 6. For each position in real space, there will be an
(infinite) set of periodic orbits passing through. The velocity trace in
planar velocity space of the above described orbits, as well as the curves
delineating some of the main resonances in the underlying axisymmetric
potential![]() , are indicated in
Figs. 7 and 8 for various azimuthal angles
, are indicated in
Figs. 7 and 8 for various azimuthal angles ![]() and a
realistic range of galactocentric distances relative to the OLR, and for two
different bar strengths. Here the angle
and a
realistic range of galactocentric distances relative to the OLR, and for two
different bar strengths. Here the angle ![]() is measured from the bar
major axis and increases towards the direction opposite to galactic rotation,
i.e. coincides with the traditional in-plane inclination angle of the bar. All
space positions are reached by many of the considered orbit families, and
sometimes several traces are produced by orbits from the same family: for
instance, at
is measured from the bar
major axis and increases towards the direction opposite to galactic rotation,
i.e. coincides with the traditional in-plane inclination angle of the bar. All
space positions are reached by many of the considered orbit families, and
sometimes several traces are produced by orbits from the same family: for
instance, at
![]() ,
there is a large range of R with three
traces from x1(1) orbits, mainly due to the loops on the x-axis of
the high-H orbits. The traces of the 1/1, 1/1 asym, x1(1),
x1*(2), x1(2) and x1*(3) orbits with non-nearly vanishing
|u|-velocity all fall very close to the associated resonance curves,
indicating that the axisymmetric approximation used to compute these curves
works well for
,
there is a large range of R with three
traces from x1(1) orbits, mainly due to the loops on the x-axis of
the high-H orbits. The traces of the 1/1, 1/1 asym, x1(1),
x1*(2), x1(2) and x1*(3) orbits with non-nearly vanishing
|u|-velocity all fall very close to the associated resonance curves,
indicating that the axisymmetric approximation used to compute these curves
works well for
![]() .
Not all resonant periodic orbits, i.e. those with
traces on the resonance curves, are unstable. In particular, orbits on the
2/1 (OLR) and 1/1 resonance curves are stable x1(1) and 1/1 orbits at
.
Not all resonant periodic orbits, i.e. those with
traces on the resonance curves, are unstable. In particular, orbits on the
2/1 (OLR) and 1/1 resonance curves are stable x1(1) and 1/1 orbits at
![]() and unstable x1*(2) and 1/1 asym orbits at
and unstable x1*(2) and 1/1 asym orbits at
![]() ,
except for a x1*(2) and a x1(1) orbit with u=0for
,
except for a x1*(2) and a x1(1) orbit with u=0for
![]() .
Hence resonance regions of phase space
are not necessary unstable and depleted as asserted in D2000 for the OLR.
.
Hence resonance regions of phase space
are not necessary unstable and depleted as asserted in D2000 for the OLR.
There are sometimes several orbits from the same family plotted very
close to each other, like for example the three unstable x1(2) orbits at
![]() ,
,
![]() and
and
![]() for F=0.20. This happens
when the sequence of orbits within the family reverses its progression in the
x-y plane towards a given direction and very close to the current space
position, causing an accumulation of orbits near this position with different
local velocities. One may also note that the continuous transitions between
some orbit families can cause periodic orbits from different families to have
almost identical traces, as for example the x1*(2) and x1(2) near the
centre of the frame
for F=0.20. This happens
when the sequence of orbits within the family reverses its progression in the
x-y plane towards a given direction and very close to the current space
position, causing an accumulation of orbits near this position with different
local velocities. One may also note that the continuous transitions between
some orbit families can cause periodic orbits from different families to have
almost identical traces, as for example the x1*(2) and x1(2) near the
centre of the frame
![]() and
and
![]() in
Fig. 8.
in
Fig. 8.
![\begin{figure}
\par\includegraphics[width=12cm]{MS1098f07.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg124.gif) |
Figure 7:
Liapunov divergence timescale of the orbits in the u-v plane as a
function of position in real space, for a bar strength F=0.10. The
horizontal and vertical axes of each frame are
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm]{MS1098f08.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg125.gif) |
Figure 8: As Fig. 7, but for a bar strength F=0.20. |
| Open with DEXTER | |
The rather large number of stable simple periodic orbits through each
space position and the numerous stellar streams observed in the Solar
neighbourhood may suggest that at least some of them are related to periodic
orbits, as anticipated in Kalnajs (1991). For instance, beside the idea of
the x1(1) and low-eccentricity x1(2) induced streams near the OLR
radius, the
![]() frames in Fig. 7 betray interesting
stable eccentric x1(2) and 5/1 asym orbits at
frames in Fig. 7 betray interesting
stable eccentric x1(2) and 5/1 asym orbits at
![]() and
and
![]() respectively and
with
respectively and
with
![]() and
and
![]() ,
which fall
very close to the velocity of the young Arcturus stream (see
Table 1).
,
which fall
very close to the velocity of the young Arcturus stream (see
Table 1).
The next step after the periodic orbit search is to determine the phase space
extent of the regular orbits trapped around the stable closed orbits and of
the chaotic orbits, which have no other integral than the Jacobi integral. The
Poincaré surface of section method is well suited to highlight the regular
and chaotic regions in phase space at constant value of the Hamiltonian, but
not at constant position in real space. A better tool for this purpose are the
Liapunov exponents, which also allow to quantify the degree of stochasticity
of the orbits. These exponents describe the mean exponential rate of
divergence of two trajectories initially close to each other in phase space
and are defined as:
The numerical computation of the Liapunov exponents faces some problems
related to the limits in Eq. (9). First, the finite initial deviation
![]() may rapidly grow as large as the size of the orbits
themselves, especially for chaotic orbits, and thus
may rapidly grow as large as the size of the orbits
themselves, especially for chaotic orbits, and thus
![]() must
be occasionally scaled down by a large factor. Noting
must
be occasionally scaled down by a large factor. Noting
![]() the deviation before the first rescaling, this is done in a way similar to
Contopoulos & Barbanis (1989), by normalising
the deviation before the first rescaling, this is done in a way similar to
Contopoulos & Barbanis (1989), by normalising
![]() to
to
![]() :
:
The Liapunov exponent ![]() has been calculated on a Cartesian grid
of planar velocities for different positions of the observer, using the 2D
potential of Eq. (5) and with an initial deviation of
has been calculated on a Cartesian grid
of planar velocities for different positions of the observer, using the 2D
potential of Eq. (5) and with an initial deviation of
![]() in the R-coordinate
(Figs. 7, 8 and 10). The results are presented
as a divergence timescale
in the R-coordinate
(Figs. 7, 8 and 10). The results are presented
as a divergence timescale
![]() in units of local
circular period in the axisymmetric part of the potential, which provides a
more obvious and useful measure of stochasticity. Diagrams have been computed
for every
in units of local
circular period in the axisymmetric part of the potential, which provides a
more obvious and useful measure of stochasticity. Diagrams have been computed
for every
![]() in azimuth for
in azimuth for
![]() ,
1.0,
1.05, 1.1, 1.2 and also at
,
1.0,
1.05, 1.1, 1.2 and also at
![]() over a larger radial range,
but those diagrams between our
over a larger radial range,
but those diagrams between our
![]() sampling and at
sampling and at
![]() will not be shown here (and the same is true for
the velocity distributions of the next section). We shall refer to such
diagrams as "Liapunov'' diagrams.
will not be shown here (and the same is true for
the velocity distributions of the next section). We shall refer to such
diagrams as "Liapunov'' diagrams.
The first thing to notice in these diagrams is that the stable and
unstable periodic orbits fall within regular and chaotic regions respectively,
as expected. There are some apparent exceptions like the 1/1 asym orbit at
![]() and large R which must owe to the limited velocity resolution of
the diagrams (=0.04
and large R which must owe to the limited velocity resolution of
the diagrams (=0.04![]() ;
see Fux 2001b for some higher resolution
Liapunov diagrams). The fraction of chaotic orbits also obviously increases
with bar strength. Furthermore, as a consequence of the four-fold symmetric
barred potential, the diagrams at
;
see Fux 2001b for some higher resolution
Liapunov diagrams). The fraction of chaotic orbits also obviously increases
with bar strength. Furthermore, as a consequence of the four-fold symmetric
barred potential, the diagrams at ![]() and
and
![]() are symmetric
with respect to u=0 and, more generally, diagrams at supplementary angles
are anti-symmetric to each other in u, i.e.
are symmetric
with respect to u=0 and, more generally, diagrams at supplementary angles
are anti-symmetric to each other in u, i.e.
![]() .
.
At
![]() and for the radial range explored in
Figs. 7 and 8, the 2/1 and 1/1 resonance curves, as
well as all other not highlighted resonances of the form
and for the radial range explored in
Figs. 7 and 8, the 2/1 and 1/1 resonance curves, as
well as all other not highlighted resonances of the form
![]() with
integer
with
integer
![]() ,
are embedded in the middle of broad regular orbit arcs
separated by mainly chaotic regions which come closer to u=0 as the bar
strength increases. For
,
are embedded in the middle of broad regular orbit arcs
separated by mainly chaotic regions which come closer to u=0 as the bar
strength increases. For
![]() (and
(and
![]() ), the regularity of the OLR arc gets destroyed near
u=0, leaving the place to an unstable x1*(2) orbit. Between the dominant
regular orbit arcs, secondary regular arcs associated with resonances of the
form
), the regularity of the OLR arc gets destroyed near
u=0, leaving the place to an unstable x1*(2) orbit. Between the dominant
regular orbit arcs, secondary regular arcs associated with resonances of the
form
![]() with odd integer
with odd integer
![]() can also be identified,
especially for F=0.10. This includes in particular the 4/1 resonance arc
visible for
can also be identified,
especially for F=0.10. This includes in particular the 4/1 resonance arc
visible for
![]() .
In fact, the chaotic regions
between the broad resonance arcs are probably densely filled by tiny arcs of
higher order regular resonant orbits, but the filling factor must be very low.
.
In fact, the chaotic regions
between the broad resonance arcs are probably densely filled by tiny arcs of
higher order regular resonant orbits, but the filling factor must be very low.
At ![]() ,
the situation is reversed: the
,
the situation is reversed: the
![]() resonance
curves lie in chaotic regions at large H which are spaced by regular orbit
arcs right between the resonances. At intermediate angles, the regular and
chaotic regions become offset from the resonance curves and the u-symmetry
breaks. In particular, for
resonance
curves lie in chaotic regions at large H which are spaced by regular orbit
arcs right between the resonances. At intermediate angles, the regular and
chaotic regions become offset from the resonance curves and the u-symmetry
breaks. In particular, for
![]() and
and
![]() ,
i.e. realistic positions for the Sun, an
extreme case of asymmetry arises near the OLR: a prominent region of regular
orbits extends down to negative u, bounded roughly by the OLR curve on the
right and penetrating well inside the hot orbit zone, whereas the positive upart of the OLR curve is surrounded by a wide chaotic region extending
somewhat inside the H12 contour and coinciding very well with the u-vlocation of the Hercules stream.
,
i.e. realistic positions for the Sun, an
extreme case of asymmetry arises near the OLR: a prominent region of regular
orbits extends down to negative u, bounded roughly by the OLR curve on the
right and penetrating well inside the hot orbit zone, whereas the positive upart of the OLR curve is surrounded by a wide chaotic region extending
somewhat inside the H12 contour and coinciding very well with the u-vlocation of the Hercules stream.
![\begin{figure}
\par\includegraphics[width=12cm]{MS1098f09.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg157.gif) |
Figure 9: Location in the u-v plane of the regular orbits trapped around the stable x1(1) periodic orbits for a bar strength F=0.20 (dark points) and around the stable x1(2) orbits for F=0.10 (grey points). The computational details are described in the text. The horizontal and vertical axes of the frames and the different curves are as in Fig. 7. The H-contours are given for F=0.10. |
| Open with DEXTER | |
Figure 9 shows the u-v region occupied by the regular orbits
trapped around the stable x1(1) and x1(2) periodic orbits. To construct
this figure, we have first derived many surfaces of section at mainly constant
Hamiltonian interval
![]() to locate the islands of
invariant curves around these periodic orbits. Then the orbits within each
islands of these maps have been sampled by 50 regularly spaced points along a
straight line across the central periodic orbit and within the outermost
invariant curve of the island. Finally, all the resulting initial conditions
are integrated for 20 rotations in the rotating frame and the velocities are
plotted when the orbits pass within a distance of
to locate the islands of
invariant curves around these periodic orbits. Then the orbits within each
islands of these maps have been sampled by 50 regularly spaced points along a
straight line across the central periodic orbit and within the outermost
invariant curve of the island. Finally, all the resulting initial conditions
are integrated for 20 rotations in the rotating frame and the velocities are
plotted when the orbits pass within a distance of
![]() of the considered space positions. The striped appearance of the regular
x1(1) and x1(2) regions in the diagrams are due to the discrete
H-sampling and the broadening of the stripes to the finite value of
of the considered space positions. The striped appearance of the regular
x1(1) and x1(2) regions in the diagrams are due to the discrete
H-sampling and the broadening of the stripes to the finite value of
![]() (not to an inaccurate orbital integration). The islands in the
surfaces of section generally contain sub-resonances which have been included.
The x1(1) islands however have been truncated at the 1/1 resonance, so
that the part of the x1(1) region on the high-v side of the 1/1resonance curve is not represented in the u-v diagrams. The x1(1) regions
are derived for F=0.20 because the high level of chaos at this bar strength
makes it easier to distinguish the boundaries of these regions in the surfaces
of section, and the x1(2) regions for F=0.10 in order to emphasise the
more regular case where these regions are larger.
(not to an inaccurate orbital integration). The islands in the
surfaces of section generally contain sub-resonances which have been included.
The x1(1) islands however have been truncated at the 1/1 resonance, so
that the part of the x1(1) region on the high-v side of the 1/1resonance curve is not represented in the u-v diagrams. The x1(1) regions
are derived for F=0.20 because the high level of chaos at this bar strength
makes it easier to distinguish the boundaries of these regions in the surfaces
of section, and the x1(2) regions for F=0.10 in order to emphasise the
more regular case where these regions are larger.
From this figure, it is obvious that the regular orbit arcs near the OLR,
and in particular the prominent regular region at
![]() and
and
![]() discussed previously, are produced by the
regular orbits around the stable periodic orbits of the x1(1) family, with
an eccentricity increasing towards larger Hamiltonian values. The regular
regions associated with the stable x1(2) orbits can be viewed as divided
into two parts, one involving only low-eccentricity orbits and the other one
the higher eccentricity orbits falling close to the 4/1 resonance curve. The
low-eccentricity orbit part exists for
discussed previously, are produced by the
regular orbits around the stable periodic orbits of the x1(1) family, with
an eccentricity increasing towards larger Hamiltonian values. The regular
regions associated with the stable x1(2) orbits can be viewed as divided
into two parts, one involving only low-eccentricity orbits and the other one
the higher eccentricity orbits falling close to the 4/1 resonance curve. The
low-eccentricity orbit part exists for
![]() and
over an angle range around
and
over an angle range around
![]() increasing as R decreases,
and is generally enclosed between the H12 contour and the OLR curve.
Elsewhere, it is dissolved and only an unstable x1*(2) orbit remains
(Fig. 7). The higher eccentricity part connects the low-eccentricity
part at
increasing as R decreases,
and is generally enclosed between the H12 contour and the OLR curve.
Elsewhere, it is dissolved and only an unstable x1*(2) orbit remains
(Fig. 7). The higher eccentricity part connects the low-eccentricity
part at
![]() and then progressively detach from
it as the 4/1 resonance curve moves away from the H12 contour at larger
R. In particular, for
and then progressively detach from
it as the 4/1 resonance curve moves away from the H12 contour at larger
R. In particular, for
![]() and for F=0.10,
there are no regular quasi-x1(2) orbits between the H12 contour
and azimuthal velocities less than
and for F=0.10,
there are no regular quasi-x1(2) orbits between the H12 contour
and azimuthal velocities less than
![]() ,
whatever the angle
,
whatever the angle
![]() ,
and no low-eccentricity such orbits at all for
,
and no low-eccentricity such orbits at all for
![]() .
Hence for this bar strength, the Hercules-like mode
found in D2000's simulations at
.
Hence for this bar strength, the Hercules-like mode
found in D2000's simulations at
![]()
![]() and
and
![]() cannot be related to such
quasi-x1(2) orbits.
cannot be related to such
quasi-x1(2) orbits.
![\begin{figure}
\par\includegraphics[width=12cm]{MS1098f10.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg169.gif) |
Figure 10:
As Fig. 7, but for
|
| Open with DEXTER | |
Figure 10 provides Liapunov diagrams over a larger radial range
at
![]() and for F=0.10. These diagrams clearly show that the
H12 contour marks the average transition between regular and chaotic
motion. Hence disc orbits are essentially regular and hot orbits essentially
chaotic. The diagrams in Fig. 10 also nicely illustrate the
dependence of the H12 and H45 contours with galactocentric distance
discussed in Sect. 3, and show how the velocity spacing between
these contours decreases with increasing R.
and for F=0.10. These diagrams clearly show that the
H12 contour marks the average transition between regular and chaotic
motion. Hence disc orbits are essentially regular and hot orbits essentially
chaotic. The diagrams in Fig. 10 also nicely illustrate the
dependence of the H12 and H45 contours with galactocentric distance
discussed in Sect. 3, and show how the velocity spacing between
these contours decreases with increasing R.
Martinet & Raboud (1999) have computed a diagram
![]() representing the relative pericentre deviation between planar orbits
integrated in a barred N-body model and the corresponding orbits in
the underlying axisymmetric potential, starting from a realistic space
position of the Sun. Their diagram correlates well with our Liapunov diagrams
in the sense that the larger values of
representing the relative pericentre deviation between planar orbits
integrated in a barred N-body model and the corresponding orbits in
the underlying axisymmetric potential, starting from a realistic space
position of the Sun. Their diagram correlates well with our Liapunov diagrams
in the sense that the larger values of ![]() coincide with shorter Liapunov
timescales. In particular, a clear jump of
coincide with shorter Liapunov
timescales. In particular, a clear jump of ![]() occurs at
occurs at
![]() ,
with the high-H side displaying much larger
pericentre deviations on the average, and there is also a tail of small
,
with the high-H side displaying much larger
pericentre deviations on the average, and there is also a tail of small
![]() -values at negative u extending inside the hot orbit region.
-values at negative u extending inside the hot orbit region.
It is worth mentioning that in a two-dimensional axisymmetric potential,
all orbits are regular, i.e. have vanishing ![]() .
Hence the chaotic
regions discussed here are all produced by the influence of the bar alone.
Also, the divergence timescale
.
Hence the chaotic
regions discussed here are all produced by the influence of the bar alone.
Also, the divergence timescale
![]() in the chaotic regions may be as
low as a few orbital times. This property may have important consequences on
the early evolution of the distribution function in barred galaxies, as we
shall see in the following section.
in the chaotic regions may be as
low as a few orbital times. This property may have important consequences on
the early evolution of the distribution function in barred galaxies, as we
shall see in the following section.
Given the orbital structure of phase space, we now want to know how nature
populates the available orbits. This is done resorting to test particle
simulations with the following two integral initial distribution function
(Dehnen 1999a):
For the time integration, D2000 uses a subtle backward integration
technique based on the conservation of the phase space density along the
orbits in collisionless systems. The idea is to integrate back in time until
t=0 the phase space points on a Cartesian grid of u-v velocities at a
given space position
![]() and time
and time
![]() ,
to
determine the energy E and angular momentum Lz of the originating orbits
in the initial axisymmetric potential, and from these infer
,
to
determine the energy E and angular momentum Lz of the originating orbits
in the initial axisymmetric potential, and from these infer
![]() .
The advantages of
this technique is that only the orbits strictly necessary to derive the
evolved local velocity distributions need to be computed, and that these
velocity distributions are not affected by Poisson noise. Moreover, a unique
simulation suffices to get u-v distributions for different initial
conditions, because
.
The advantages of
this technique is that only the orbits strictly necessary to derive the
evolved local velocity distributions need to be computed, and that these
velocity distributions are not affected by Poisson noise. Moreover, a unique
simulation suffices to get u-v distributions for different initial
conditions, because ![]() comes in only after the orbit
integration.
comes in only after the orbit
integration.
Unfortunately, the backward integration technique faces two major
problems illustrated in Fig. 11, which shows the long term
evolution of the planar velocity distribution at
![]() and
and
![]() using this
technique. The integration time in D2000 ranges from 4 bar rotation for most
simulations, corresponding to only
using this
technique. The integration time in D2000 ranges from 4 bar rotation for most
simulations, corresponding to only ![]() 2 orbital periods at
2 orbital periods at
![]() in the inertial frame, up to 8 bar rotation for some cases, but always
matching the growth time of the bar to half the total integration time. The
frame at
in the inertial frame, up to 8 bar rotation for some cases, but always
matching the growth time of the bar to half the total integration time. The
frame at
![]() is similar to his results, revealing a clear bimodal
distribution. However, at
is similar to his results, revealing a clear bimodal
distribution. However, at
![]() ,
the valley between the two modes
becomes heavily populated, destroying the bimodality, and at later times,
incurved waves appear in this valley with a spacing between the maxima
decreasing with time. This is a typical signature of ongoing phase mixing in a
regular region of phase space, which here corresponds to the eccentric orbit
part of the quasi-x1(1) region according to the previous section. A
very similar phenomenon, with similarly incurved waves, can also be barely
recognised near the 1/1 resonance. Between the 2/1 and 1/1 resonances,
phase mixing operates on a shorter timescale and the orientation of the wave
fronts seems to change from nearly-vertical at
,
the valley between the two modes
becomes heavily populated, destroying the bimodality, and at later times,
incurved waves appear in this valley with a spacing between the maxima
decreasing with time. This is a typical signature of ongoing phase mixing in a
regular region of phase space, which here corresponds to the eccentric orbit
part of the quasi-x1(1) region according to the previous section. A
very similar phenomenon, with similarly incurved waves, can also be barely
recognised near the 1/1 resonance. Between the 2/1 and 1/1 resonances,
phase mixing operates on a shorter timescale and the orientation of the wave
fronts seems to change from nearly-vertical at
![]() to
nearly-horizontal at
to
nearly-horizontal at
![]() .
The backward integration technique in
fact yields the fine-grained distribution function, which never smoothes out
on sufficiently small scales, whereas the physical one to compare with the
observations is the coarse-grained distribution. The second problem is related
to chaos: at
.
The backward integration technique in
fact yields the fine-grained distribution function, which never smoothes out
on sufficiently small scales, whereas the physical one to compare with the
observations is the coarse-grained distribution. The second problem is related
to chaos: at
![]() ,
the u-v distribution becomes noisy in the
chaotic regions because the phase space points integrated backwards from these
regions sample the initial distribution function more randomly. Hence much
longer integration times than in D2000 are required to obtain
quasi-equilibrium (coarse-grained) distribution functions and to properly take
into account the effect of chaos (remember that the divergence timescales for
chaotic orbits is of the order of several orbital periods), and one cannot
escape the fate of smoothing the fine-grained distribution.
,
the u-v distribution becomes noisy in the
chaotic regions because the phase space points integrated backwards from these
regions sample the initial distribution function more randomly. Hence much
longer integration times than in D2000 are required to obtain
quasi-equilibrium (coarse-grained) distribution functions and to properly take
into account the effect of chaos (remember that the divergence timescales for
chaotic orbits is of the order of several orbital periods), and one cannot
escape the fate of smoothing the fine-grained distribution.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS1098f11.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg199.gif) |
Figure 11:
Time evolution of the velocity distribution in the u-v plane at
|
| Open with DEXTER | |
Therefore, most of the test particle simulations in this paper were done
by simple forward integration. The initial phase space density is sampled by
N particles which are then integrated forward in time, and the u-vdiagrams at space position
![]() are constructed from all the
particles within a distance
are constructed from all the
particles within a distance
![]() from that position
(corresponding to
from that position
(corresponding to
![]() pc for
pc for
![]() kpc), using a
Cartesian velocity binning with a bin size of
kpc), using a
Cartesian velocity binning with a bin size of
![]() .
To increase
the particle statistics, the u-v distributions are averaged over 10 bar
rotations and then smoothed within a square of
.
To increase
the particle statistics, the u-v distributions are averaged over 10 bar
rotations and then smoothed within a square of
![]() bins. The time
average, which is hardly possible in the backward integration technique, is
also very convenient to reduce the phase mixing problem, as the contribution
of each particle to a u-v distribution becomes proportional to the time
the particle spends within the volume where the distribution is computed.
With the forward integration technique, the time evolution of the velocity
distribution can be followed within a unique simulation. The test particle
simulations of this paper all have N=106 and the velocity distributions
have been derived within two time intervals,
bins. The time
average, which is hardly possible in the backward integration technique, is
also very convenient to reduce the phase mixing problem, as the contribution
of each particle to a u-v distribution becomes proportional to the time
the particle spends within the volume where the distribution is computed.
With the forward integration technique, the time evolution of the velocity
distribution can be followed within a unique simulation. The test particle
simulations of this paper all have N=106 and the velocity distributions
have been derived within two time intervals,
![]() and
and
![]() .
Since the distance parameters in
.
Since the distance parameters in ![]() scale as
scale as ![]() and not
and not
![]() ,
the results at different
,
the results at different
![]() require distinct simulations.
require distinct simulations.
Figure 12 shows the u-v distributions at various space
positions averaged over the time interval
![]() for a
bar strength F=0.10. As for the Liapunov diagrams, the distributions are
obviously symmetric with respect to u=0 for
for a
bar strength F=0.10. As for the Liapunov diagrams, the distributions are
obviously symmetric with respect to u=0 for ![]() and
and
![]() and the distributions at same radius but supplementary
angles are anti-symmetric to each other in u. This is clearly not the case
in the simulations of D2000 (see his Fig. 2, where F=0.089), providing a
further argument that these have not achieved a quasi-stationary regime.
Moreover, the traces of the stable x1(1) periodic orbits away from the
2/1 resonance curve lie closer to the high angular momentum peak of the
velocity distributions.
For this bar strength and the adopted values of the
parameters in the initial distribution function, there is also no clear
bimodality with a deep separation valley at
and the distributions at same radius but supplementary
angles are anti-symmetric to each other in u. This is clearly not the case
in the simulations of D2000 (see his Fig. 2, where F=0.089), providing a
further argument that these have not achieved a quasi-stationary regime.
Moreover, the traces of the stable x1(1) periodic orbits away from the
2/1 resonance curve lie closer to the high angular momentum peak of the
velocity distributions.
For this bar strength and the adopted values of the
parameters in the initial distribution function, there is also no clear
bimodality with a deep separation valley at
![]() and near
and near
![]() ,
although a clear density excess remains at low v and positive
u
,
although a clear density excess remains at low v and positive
u![]() . However, all space positions where
a low-eccentricity regular x1(2) region exists (see former section and
Fig. 9) present a nice bimodality, with the low angular momentum mode
coinciding very well with that region and always peaking inside the H12contour.
. However, all space positions where
a low-eccentricity regular x1(2) region exists (see former section and
Fig. 9) present a nice bimodality, with the low angular momentum mode
coinciding very well with that region and always peaking inside the H12contour.
While the traces of the non-resonant x1(1) and x1(2) orbits are
generally embedded within their associated quasi-periodic orbit modes, they do
not necessarily exactly coincide with the peak of these modes, especially in
the x1(2) case (e.g.
![]() and
and
![]() -
-
![]() in Fig. 12). Furthermore, since the
quasi-periodic orbits cover a larger space area than the periodic orbits
themselves, quasi-x1(1) and quasi-x1(2) modes may occur
even at positions where no x1(1) or x1(2) orbit are passing through.
in Fig. 12). Furthermore, since the
quasi-periodic orbits cover a larger space area than the periodic orbits
themselves, quasi-x1(1) and quasi-x1(2) modes may occur
even at positions where no x1(1) or x1(2) orbit are passing through.
Increasing the bar strength (Fig. 13) provides a better
understanding of how the velocity distributions are affected by chaos. Now,
there appears to be an obvious second source producing a low angular momentum
mode, which adds to the quasi-x1(2) orbit flow at the space regions
reached by these orbits, and acts alone elsewhere, as for instance at
![]() and
and
![]() .
The overdensity
in velocity space generated by this second source correlates very well with
highly stochastic regions in the Liapunov diagrams (see Fig. 8) and
seems to always peak outside the H12 contour. At
.
The overdensity
in velocity space generated by this second source correlates very well with
highly stochastic regions in the Liapunov diagrams (see Fig. 8) and
seems to always peak outside the H12 contour. At
![]() ,
the overdensity culminates at
,
the overdensity culminates at
![]() and is enclosed by the regular arc
of eccentric quasi-x1(1) orbits. At
and is enclosed by the regular arc
of eccentric quasi-x1(1) orbits. At ![]() ,
these
quasi-x1(1) orbits occupy the u=0 region and chaotic overdensities
happen symmetrically on both positive and negative u sides of this region.
At
,
these
quasi-x1(1) orbits occupy the u=0 region and chaotic overdensities
happen symmetrically on both positive and negative u sides of this region.
At
![]() ,
the quasi-x1(1) region is located at
negative u and there is a large chaotic overdensity at positive u.
,
the quasi-x1(1) region is located at
negative u and there is a large chaotic overdensity at positive u.
These properties result from the decoupling between the regular and the
chaotic regions of phase space. Since chaotic orbits cannot visit the regions
of regular motion and, vice versa, regular orbits avoid the chaotic regions,
the distribution function in each of these regions evolves in a completely
independent way. In the regular regions, it recovers roughly the initial
distribution after phase mixing, whereas in the chaotic regions, it is
substantially modified through a process known as chaotic mixing and
which operates on the Liapunov divergence timescale (e.g. Kandrup 2001):
the particles on chaotic orbits quickly disperse within the easily accessible
phase space regions, i.e. not impeded by cantori or an Arnold web, and
converge towards a uniform population of these regions. The dominant
manifestation of chaotic mixing is a net migration of particles from the inner
to the outer space regions. For instance, in the simulations with
![]() ,
the scale length of the radial particle
distribution, which remains very close to an exponential in the range
,
the scale length of the radial particle
distribution, which remains very close to an exponential in the range
![]() ,
increases by
,
increases by ![]() 30% for F=0.10 and by
30% for F=0.10 and by
![]() 90% for F=0.20 within this radial range. This migration is
particularly marked for particles on hot chaotic orbits because the region
inside corotation initially represents a large reservoir of such particles and
because these particles can freely pass over corotation. As a consequence, in
the explored
90% for F=0.20 within this radial range. This migration is
particularly marked for particles on hot chaotic orbits because the region
inside corotation initially represents a large reservoir of such particles and
because these particles can freely pass over corotation. As a consequence, in
the explored
![]() range, the chaotic regions in
the u-v diagrams are more heavily crowded than the regular regions at
range, the chaotic regions in
the u-v diagrams are more heavily crowded than the regular regions at
![]() ,
therefore corresponding to local overdensities.
,
therefore corresponding to local overdensities.
At first glance, there seems to be a rather continuous transition from
the quasi-x1(2) orbit mode to the main chaotic orbit mode when
moving across the OLR radius towards increasing ![]() ,
with always a
single effective peak showing up and with the involved quasi-x1(2)
region progressively dissolving in the chaotic one. But in some cases, the two
mode-generating sources really contribute to distinct peaks in the velocity
distribution (see Fig. 20d for an example).
,
with always a
single effective peak showing up and with the involved quasi-x1(2)
region progressively dissolving in the chaotic one. But in some cases, the two
mode-generating sources really contribute to distinct peaks in the velocity
distribution (see Fig. 20d for an example).
The process of chaotic mixing leads to velocity distribution contours
which are parallel to the contours of constant H in the chaotic regions
(e.g. Fig. 13). This property is also consistent with Jean's theorem
stating that the distribution function in a steady-state system depends only
on the integral of motions. The only integral for the chaotic orbits in the
present 2D barred models is the value of the Hamiltonian, hence the
distribution function and therefore the corresponding velocity distributions
at fixed space position should be a function of only H in the chaotic
regions. It should be noted that the Jeans theorem does not strictly apply to
the hot and disc chaotic orbits. Indeed, these orbits are not energetically
bound (in terms of H) and thus the phase space density around such orbits
and within the finite space volume of the galaxy should decrease with time,
conflicting with the steady-state assumption of the theorem. However, the
escaping timescale of these chaotic orbits, which is essentially controlled by
Arnold diffusion across the confining cantori, is much longer than the
Liapunov divergence timescale and even the Hubble time, and thus the density
in the phase space regions covered by these orbits can be considered as almost
constant (see also Kaufmann & Contopoulos 1996 and references therein).
![\begin{figure}
\par\includegraphics[width=13cm]{MS1098f12.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg212.gif) |
Figure 12: Velocity distribution in the u-v plane as a function of space position in the test particle simulations with a bar strength F=0.10. The distributions are time averages within the interval from 25 to 35 bar rotations after the beginning of the simulations. The velocity contours are as in Fig. 1, whereas the axis labels, the Hamiltonian contours, the resonance curves and the periodic orbits are as in Fig. 7. |
| Open with DEXTER | |
Secondary chaotic orbit overdensities also occur between the x1(1) and
the 1/1 regular arcs, especially at
![]() and
and
![]() (Fig. 13). These
secondary overdensities and the above described main overdensities connect to
each other in phase space, i.e. are traced by the same orbits. Hence it is
also expected that the u-v density at constant H-value is the same for all
overdensities. This is only roughly the case in Fig. 13, probably
because the smoothing of the diagrams lowers the peaks of the tiny secondary
overdensities relative to the broader main overdensities. Small chaotic
overdensities may sometimes even be noticed beyond the 1/1 resonance curve.
However, at high angular momentum, the hot orbits spend most of their time in
the outer galaxy, far away from the influence of the bar, and thus become more
regular (the energy and angular momentum are more nearly conserved). The
eccentric x1(2) regular regions can also represent density depressions
between chaotic regions in the velocity distributions, as can be marginally
inferred for example from the
(Fig. 13). These
secondary overdensities and the above described main overdensities connect to
each other in phase space, i.e. are traced by the same orbits. Hence it is
also expected that the u-v density at constant H-value is the same for all
overdensities. This is only roughly the case in Fig. 13, probably
because the smoothing of the diagrams lowers the peaks of the tiny secondary
overdensities relative to the broader main overdensities. Small chaotic
overdensities may sometimes even be noticed beyond the 1/1 resonance curve.
However, at high angular momentum, the hot orbits spend most of their time in
the outer galaxy, far away from the influence of the bar, and thus become more
regular (the energy and angular momentum are more nearly conserved). The
eccentric x1(2) regular regions can also represent density depressions
between chaotic regions in the velocity distributions, as can be marginally
inferred for example from the
![]() and
and
![]() frame in Figs. 9 and 12.
frame in Figs. 9 and 12.
The valley between the main high-Lz velocity mode (or LSR mode after
Dehnen) and the main chaotic orbit mode is generally close to the H12contour, reflecting the decline of the hot orbit population as
![]() .
Such a valley should in principle also exist between
the LSR mode and the secondary chaotic overdensities (see for instance
.
Such a valley should in principle also exist between
the LSR mode and the secondary chaotic overdensities (see for instance
![]() and
and
![]() in
Fig. 13). The main chaotic orbit mode also seems to always peak
between the H12 and H45 contours in Fig. 13, but this is
not true for all our test particle simulations, as demonstrated by the
in
Fig. 13). The main chaotic orbit mode also seems to always peak
between the H12 and H45 contours in Fig. 13, but this is
not true for all our test particle simulations, as demonstrated by the
![]() frame in Figs. 14 and 20a. However,
this property might be more generic for self-consistent models (see
Sect. 10). For some not fully understood reasons, the symmetry
properties mentioned previously for the case F=0.10 are somewhat less
evident for F=0.20, despite the longer integration time.
frame in Figs. 14 and 20a. However,
this property might be more generic for self-consistent models (see
Sect. 10). For some not fully understood reasons, the symmetry
properties mentioned previously for the case F=0.10 are somewhat less
evident for F=0.20, despite the longer integration time.
D2000 attributes the valley between the main LSR mode and the
Hercules-like mode to stars scattered off the OLR, in the sense that the
resonance generates chaotic orbits. In particular, he claims that the unstable
x1*(2) orbit falls exactly between the two modes. This is not quite
correct for a stochastically induced Hercules-like mode, as is best
illustrated by Fig. 13: for
![]() and
and
![]() ,
the u>0 part of the 2/1 resonance curve
passes through the Hercules-like mode and the x1*(2) orbit clearly lies
within the mode at
,
the u>0 part of the 2/1 resonance curve
passes through the Hercules-like mode and the x1*(2) orbit clearly lies
within the mode at
![]() ,
and the low density
region below this mode is due to regular resonant orbits. D2000 also
claims that in his simulations the extension of the LSR mode to u<0 at
,
and the low density
region below this mode is due to regular resonant orbits. D2000 also
claims that in his simulations the extension of the LSR mode to u<0 at
![]() is caused by the elongation of the (presumably
quasi-x1(1)) orbits near the OLR. Our results indicate that at least
the final part of this extension, corresponding to the secondary
overdensities, is produced by chaotic orbits. Such an extension exits in the
observations, but is only significant down to heliocentric
is caused by the elongation of the (presumably
quasi-x1(1)) orbits near the OLR. Our results indicate that at least
the final part of this extension, corresponding to the secondary
overdensities, is produced by chaotic orbits. Such an extension exits in the
observations, but is only significant down to heliocentric
![]() kms-1.
kms-1.
The velocity distributions at the two different mean integration times
![]() and
and
![]() reveal some secular evolution. As
reveal some secular evolution. As
![]() increases, the crowding contrast between the regular and chaotic
regions becomes more evident, with denser high-H chaotic regions and deeper
regular region valleys. The quasi-x1(1) mode squeezes towards its high
angular momentum side for
increases, the crowding contrast between the regular and chaotic
regions becomes more evident, with denser high-H chaotic regions and deeper
regular region valleys. The quasi-x1(1) mode squeezes towards its high
angular momentum side for
![]() and,
especially in the case F=0.10, the peak of the quasi-x1(2) mode
moves closer to the H12 contour for
and,
especially in the case F=0.10, the peak of the quasi-x1(2) mode
moves closer to the H12 contour for
![]() ,
betraying a longer phase mixing timescale near this resonance
,
betraying a longer phase mixing timescale near this resonance![]() .
.
In a real galaxy, the presence of mass concentrations like giant molecular clouds and of transient spiral arms will prevent the strict conservation of the Jacobi integral and cause the stars to diffuse from the regular regions to the chaotic regions of phase space and vice versa (see also Sect. 10). The chaotic regions should be very efficient in heating galactic discs and the communication between the two kind of regions may even allow to heat regular regions. The quantification of this phenomenon might be an interesting problem to study, but is beyond the scope of this paper.
Finally, Figs. 12 and 13 also suggest that with
increasing bar strength, the velocity dispersion ratio
![]() decreases and, as reported by D2000, the u-range and in particular the mean
u-velocity of the main chaotic overdensity become larger.
decreases and, as reported by D2000, the u-range and in particular the mean
u-velocity of the main chaotic overdensity become larger.
![\begin{figure}
\par\includegraphics[width=13cm]{MS1098f13.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg228.gif) |
Figure 13:
Same as Fig. 12, but for a bar strength F=0.20 and a time
average over the interval
|
| Open with DEXTER | |
How can the initial conditions be changed in order to increase the population
of the hot chaotic orbits, and in particular the density in the Hercules-like
chaotic overdensity? Figure 14 shows how the three parameters of the
initial axisymmetric distribution function (Eq. (12)) individually
affect the final velocity distribution for a realistic position of the Sun and
F=0.10, using exceptionally the backward integration technique which, as
mentioned in Sect. 7, is very convenient for this purpose. A long
time integration is adopted to reduce the phase mixing problem and the u-vdistributions are smoothed the same way as the previous ones based on the
direct integration method. A comparison of the default parameter velocity
distribution with the corresponding distribution (at
![]() )
in
Fig. 12 indicates that both integration techniques give very similar
results.
)
in
Fig. 12 indicates that both integration techniques give very similar
results.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS1098f14.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg229.gif) |
Figure 14:
Velocity distribution in the u-v plane after 120 bar rotations as
a function of initial conditions and using the backward integration technique.
The space position is
|
| Open with DEXTER | |
Increasing the overall initial velocity dispersion (top frames in
Fig. 14) yields a larger final
velocity dispersion. Hence in this kind of simulations the particles remember
the initial conditions and the action of the bar is unable to completely erase
them. Also, the u-v density in the Hercules-like stream is enhanced relative
to the density within the main velocity mode. This is because the larger
velocity dispersion lowers the peak of the latter mode, and because a larger
![]() increases the average Hamiltonian value of the
particles and thus the fraction of hot chaotic particles. Reducing the initial
velocity dispersion scale length keeping the same velocity dispersion at
increases the average Hamiltonian value of the
particles and thus the fraction of hot chaotic particles. Reducing the initial
velocity dispersion scale length keeping the same velocity dispersion at
![]() (middle frames) renders the inner regions hotter and hence mainly
increases the density of the velocity distribution at low angular momentum. To
increase the relative fraction of stars in the Hercules-like stream, the most
efficient way seems to start with a smaller disc scale length (bottom frames).
This represents a higher initial space density of the disc in the inner
regions where the particles have larger H-values on the average and thus
again a larger fraction of hot chaotic particles which will be spread over the
whole disc by the barred potential.
(middle frames) renders the inner regions hotter and hence mainly
increases the density of the velocity distribution at low angular momentum. To
increase the relative fraction of stars in the Hercules-like stream, the most
efficient way seems to start with a smaller disc scale length (bottom frames).
This represents a higher initial space density of the disc in the inner
regions where the particles have larger H-values on the average and thus
again a larger fraction of hot chaotic particles which will be spread over the
whole disc by the barred potential.
By changing the initial conditions, it is therefore possible to achieve a more pronounced main chaotic overdensity than in the results based on the default parameters and also to match more precisely the observed velocity dispersions in the Solar neighbourhood.
A worthful exercise is to determine what happens to the periodic orbits which
are initially in (outer) 2/1 resonance before the growth of the bar. This is
illustrated in Fig. 15, which highlights for two different space
positions at
![]() the points in the u-v plane corresponding to
trajectories which were on such orbits at t=0. The diagrams are built by
integrating backwards the trajectories passing through a Cartesian u-v grid
and marking all the points on this grid originating from initial orbits with
the points in the u-v plane corresponding to
trajectories which were on such orbits at t=0. The diagrams are built by
integrating backwards the trajectories passing through a Cartesian u-v grid
and marking all the points on this grid originating from initial orbits with
![]() .
The
darkness of the points reflects the angle
.
The
darkness of the points reflects the angle ![]() between the major axis of
the initial resonant orbit and the major axis of the then vanishing bar
potential, with darker points standing for smaller angles, i.e. resonant
orbits with apocentre closer to the bar major axis.
between the major axis of
the initial resonant orbit and the major axis of the then vanishing bar
potential, with darker points standing for smaller angles, i.e. resonant
orbits with apocentre closer to the bar major axis.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS1098f15.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg231.gif) |
Figure 15:
For two different space positions and after 120 bar rotations,
traces in the u-v plane of the trajectories which were in OLR with the
unperturbed rotating potential at t=0 (bar strength F=0.10). The points
are colour-coded according to the angle |
| Open with DEXTER | |
At
![]() and
and
![]() ,
there is a wide
region of regular orbits around most of the 2/1 resonance curve (see
Fig. 7). The trajectories with small
,
there is a wide
region of regular orbits around most of the 2/1 resonance curve (see
Fig. 7). The trajectories with small ![]() 's clearly fall in the
inner part of this region, while those with larger
's clearly fall in the
inner part of this region, while those with larger ![]() 's appear rather on
its edge and are spread within the neighbouring chaotic regions. In addition
to the regular versus chaotic phase space decoupling, the fact that the OLR
curve is associated with a valley in the planar velocity distribution (see
Fig. 12) is also because the phase space density in the chaotic
regions bounding the regular orbit arc around this curve is forced to be a
function of H only, hence lowering the density on the low-v side and
increasing it on the other side relative to the initial densities. At
's appear rather on
its edge and are spread within the neighbouring chaotic regions. In addition
to the regular versus chaotic phase space decoupling, the fact that the OLR
curve is associated with a valley in the planar velocity distribution (see
Fig. 12) is also because the phase space density in the chaotic
regions bounding the regular orbit arc around this curve is forced to be a
function of H only, hence lowering the density on the low-v side and
increasing it on the other side relative to the initial densities. At
![]() and
and
![]() ,
the part of the 2/1resonance curve within the u>0 chaotic region has no nearby small-
,
the part of the 2/1resonance curve within the u>0 chaotic region has no nearby small-![]() points and is embedded in a broad cloud of high-
points and is embedded in a broad cloud of high-![]() points.
points.
Hence, the initial 2/1 resonant orbits more nearly aligned with the bar major axis end into regular regions, while only those more nearly perpendicular to this axis are scattered into chaotic regions. This is consistent with the stability properties of the low-eccentricity x1(1) and x1*(2) orbits in the full barred potential, which are both 2/1 periodic orbits.
In addition to the test particle simulations, we have also run a
high-resolution N-body simulation whose predictions can be compared
with the results of the former sections. The main difference of this
simulation with respect to the previous simulations is that it is
three-dimensional and completely self-consistent, i.e. with no rigid component
and allowing the development of spiral arms. The description of the simulation
hereafter is based on physical units in which the initial conditions provide a
reasonable axisymmetric model of the present Milky Way. In these units,
![]() kpc at t=2.32 Gyr.
kpc at t=2.32 Gyr.
The simulation, also discussed in Fux (2000), is similar to the
simulations presented in Fux (1997), starting from a bar unstable
axisymmetric model including a nucleus-spheroid, a disc and a dark halo
component with parameters set to a=1 kpc,
![]() ,
,
![]() kpc, hz=300 pc,
kpc, hz=300 pc,
![]() ,
b=9.1 kpc and
,
b=9.1 kpc and
![]() (in the same notation as in Fux
1997). It involves
(in the same notation as in Fux
1997). It involves
![]() particles of which
particles of which
![]() belong
to the disc component. The simulation uses the double polar-cylindrical grid
technique described in Fux (1999) to solve the gravitational forces, with
belong
to the disc component. The simulation uses the double polar-cylindrical grid
technique described in Fux (1999) to solve the gravitational forces, with
![]() ,
Hz=25 pc and imposed
reflection symmetry with respect to the plane z=0 and the z-axis.
The time integrator is a leap-frog with a time step
,
Hz=25 pc and imposed
reflection symmetry with respect to the plane z=0 and the z-axis.
The time integrator is a leap-frog with a time step
![]() Myr. The
simulation has been carried out until t=2.65 Gyr. The phase space
coordinates have been saved every 50 Myr for all particles and every Myr for
the disc particles within a fixed annulus
Myr. The
simulation has been carried out until t=2.65 Gyr. The phase space
coordinates have been saved every 50 Myr for all particles and every Myr for
the disc particles within a fixed annulus
![]() .
.
After the formation of the bar at about 1.4 Gyr, the simulation reveals
a complex velocity structure with multiple streams occuring almost everywhere
in the disc. The streams, as well as the velocity dispersions, remain very
time dependent, even within space regions corotating with the bar. Some mpeg
movies showing the time evolution of the u-v distribution for a realistic
position of the Sun are available on the web at the address
http://www.mso.anu.edu.au/~fux/streams.html. However, the strong time dependency is certainly partly the consequence of
incomplete phase mixing as in the test particle simulations of the previous
sections. Therefore, we will again average in time the u-v distributions
resulting from the N-body simulation to minimise this problem and
thus focus on the average properties of these distributions.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS1098f16.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg244.gif) |
Figure 16:
Some properties of the N-body simulation averaged over
|
| Open with DEXTER | |
A complication arises from the fact that the pattern speed of the bar
decreases with time due to the angular momentum the bar loses to the (live)
dark halo, so that the OLR does not lie at a fixed radius anymore but moves
outwards. The decrease of
![]() is probably not that large in real
disc galaxies with a substantial gas fraction like the Milky Way, as shown by
self-consistent numerical simulations with an SPH component (e.g. Friedli &
Benz 1993). Hence, the u-v distributions at a given
is probably not that large in real
disc galaxies with a substantial gas fraction like the Milky Way, as shown by
self-consistent numerical simulations with an SPH component (e.g. Friedli &
Benz 1993). Hence, the u-v distributions at a given
![]() must be computed within space volumes
comoving with
must be computed within space volumes
comoving with
![]() .
We found that the evolution of the bar
position angle
.
We found that the evolution of the bar
position angle
![]() over the time interval
over the time interval
![]() can be well fitted by an analytical function of
the form:
can be well fitted by an analytical function of
the form:
 |
(13) |
| |
Figure 17:
a) Characteristic diagram for the low-eccentricity x1(1),
x1*(2) and x1(2) periodic orbits in the time averaged N-body
model. The full and dotted lines indicate stable and unstable orbits
respectively, and the dashed line the zero velocity curve.
|
| Open with DEXTER | |
The time average is done over the interval
![]() and as underlying mass distribution and potential associated with the average
velocity distributions, we take those resulting from the sum of the 50 Myr
spaced output models of the simulation within the same time interval and with
the mass in each model rescaled as the distances to preserve the velocity
scale. The number of models added together is rather low (only 14), yielding
only a crude estimate of the true average quantities, especially regarding
azimuthal variations in the spiral arm regions. Figure 16 shows some
properties of the resulting average model. At given radius R, the azimuthal
and radial bar strengths
and as underlying mass distribution and potential associated with the average
velocity distributions, we take those resulting from the sum of the 50 Myr
spaced output models of the simulation within the same time interval and with
the mass in each model rescaled as the distances to preserve the velocity
scale. The number of models added together is rather low (only 14), yielding
only a crude estimate of the true average quantities, especially regarding
azimuthal variations in the spiral arm regions. Figure 16 shows some
properties of the resulting average model. At given radius R, the azimuthal
and radial bar strengths
![]() and
and
![]() (Fig. 16e) are
defined as the most extreme values over azimuth of
(Fig. 16e) are
defined as the most extreme values over azimuth of
![]() and
and
![]() respectively, where
respectively, where
![]() and
and ![]() are the azimuthal and radial accelerations in the plane
z=0 and
are the azimuthal and radial accelerations in the plane
z=0 and
![]() is the axisymmetric part of
is the axisymmetric part of ![]() .
In particular,
.
In particular,
![]() coincides with the definition of bar
strength used in the former sections. The time averaged model has
coincides with the definition of bar
strength used in the former sections. The time averaged model has
![]() ,
i.e. a rather strong bar. However, Buta &
Block (2001) have introduced a bar strength classification in terms of a
parameter
,
i.e. a rather strong bar. However, Buta &
Block (2001) have introduced a bar strength classification in terms of a
parameter ![]() ,
corresponding here to the radial maximum of
,
corresponding here to the radial maximum of
![]() ,
and present galaxies with values of this parameter up to
0.65. Our average model has
,
and present galaxies with values of this parameter up to
0.65. Our average model has
![]() and thus falls only in
the middle of the range covered by real galaxies.
and thus falls only in
the middle of the range covered by real galaxies.
The disc scale length between corotation and slightly outside the OLR (Fig. 16a) has substantially increased with respect to the initial conditions, in agreement with the test particle results. The effective potential (Fig. 16b) indicates Lagrangian points which significantly lag the bar principal axes. This is the effect of the spiral arms starting at the end of the bar, which were absent in the test particle simulations and now produce a twist of the potential well. Note however that, as pointed out by Zhang (1996), there is a phase shift between the potential and the density wells, with the former leading the latter outside the bar. The characteristic curves of the main periodic orbit families and the x-yconfiguration of the x1(1) orbits in the average potential are given in Fig. 17. The characteristic curves are truncated at large H, where they start to bend and interfere with each other presumably as a consequence of the sharp phase change in the potential well at large radii (see Fig. 16b). The x1(1) orbits respond to the twisted potential well by having their major axis departing more and more from the y-axis as H decreases, and the closed orbits of the other families share a similar response. Since the cusps of the cusped orbits now occur away from the coordinate axes, the characteristic curves no longer reach the ZVC.
The time averaged u-v distributions are presented in Fig. 18.
The diagrams are computed by summing the 1 Myr spaced outputs of the
simulation, yielding much more accurate time averages than for the properties
based on the 50 Myr spaced outputs, and using the same space volumes,
velocity binning and smoothing procedure as for the test particle simulations.
However, contrary to the latter simulations, the diagrams are based on a
unique simulation and therefore the initial conditions for each diagram now
scale as
![]() instead of
instead of ![]() .
Hence the pattern
speed and size of the bar are not the only parameters that change for
different values of
.
Hence the pattern
speed and size of the bar are not the only parameters that change for
different values of
![]() .
In particular, the
initial velocity dispersions decrease with R, causing a similar trend in the
final velocity distributions. Diagrams have been derived at an azimuthal
interval
.
In particular, the
initial velocity dispersions decrease with R, causing a similar trend in the
final velocity distributions. Diagrams have been derived at an azimuthal
interval
![]() ,
but only those at
,
but only those at
![]() spacing
are shown.
spacing
are shown.
![\begin{figure}
\par\includegraphics[width=13cm]{MS1098f18.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg271.gif) |
Figure 18:
Time averaged planar velocity distribution of the disc particles in
the N-body simulation as a function of position in space and within
vertical cylinders of radius
|
| Open with DEXTER | |
A priori, some properties inferred from the test particle simulations
seem less robust in the N-body simulation: the non-resonant x1(1)orbits are somewhat less coincident with peaks in the velocity distributions,
and the resonant x1(1) orbits, i.e. those with traces on the 2/1resonance curve, are less correlated with depleted u-v regions at high
eccentricities. Moreover, the low angular momentum peak often lies well inside
the hot orbit region even when it is still mostly associated with regular
quasi-x1(2) orbits, as indicated by the presence of a stable
low-eccentricity x1(2) orbit. In fact, a closer inspection reveals that the
velocity distributions in the N-body simulation at given
![]() appear to best match those of the test
particle simulations at a typically 10% larger value of
appear to best match those of the test
particle simulations at a typically 10% larger value of
![]() .
This can be explained by a delayed response
of the phase space density distribution to the growing absolute OLR radius:
the u-v distributions do not instantaneously adjust to the moving
.
This can be explained by a delayed response
of the phase space density distribution to the growing absolute OLR radius:
the u-v distributions do not instantaneously adjust to the moving
![]() and therefore always reflect an earlier smaller
and therefore always reflect an earlier smaller
![]() value instead of the current one. Hence the velocity
distributions in Fig. 18 should virtually be shifted upwards by
roughly one frame to be more consistent with the
value instead of the current one. Hence the velocity
distributions in Fig. 18 should virtually be shifted upwards by
roughly one frame to be more consistent with the
![]() scale and the other plotted informations.
Actually, the effective
scale and the other plotted informations.
Actually, the effective
![]() must be a function of the
orbits.
must be a function of the
orbits.
With such a correction in mind, the N-body velocity
distributions now share much more the same properties as in the test particle
simulations. The low angular momentum mode, when purely induced by chaotic
orbits as in the frame
![]() and
and
![]() of Fig. 18, also no longer peaks outside the
H45 contour, but rather between the H12 and the H45 contours.
The velocity distributions most resemble those of the test particle
simulations with a bar strength F=0.15 (not shown in this paper, but see
Fux 2001a). Since
of Fig. 18, also no longer peaks outside the
H45 contour, but rather between the H12 and the H45 contours.
The velocity distributions most resemble those of the test particle
simulations with a bar strength F=0.15 (not shown in this paper, but see
Fux 2001a). Since
![]() in our average N-body model,
this suggests that the velocity distributions are less responsive to the bar
strength in the more realistic 3D N-body simulation than in the 2D
test particle simulations.
in our average N-body model,
this suggests that the velocity distributions are less responsive to the bar
strength in the more realistic 3D N-body simulation than in the 2D
test particle simulations.
The symmetries found in Sect. 7 for the velocity
distributions, and in particular the u-symmetry at ![]() and
and
![]() ,
obviously break and the velocity distributions in the
N-body model at given
,
obviously break and the velocity distributions in the
N-body model at given ![]() and fixed effective radius seem to
compare best with the corresponding distributions in the test particle
simulations at an angle
and fixed effective radius seem to
compare best with the corresponding distributions in the test particle
simulations at an angle
![]() ,
suggesting that the velocity
distributions know about the spiral arm induced average local twist of the
potential well relative to the bar major axis. While this is especially true
for the more regular low-H regions, the velocity distributions show no
significant phase shift at all in the hot orbit region. The reason is because
the hot orbits are more eccentric and therefore are sensitive to more inner
features of the potential. It should be noted that in N-body
simulations like the one presented here, spiral arms are particularly strong
during about 1 Gyr after the formation of the bar, so that the reported
effects of spiral arms are probably overestimates for the Milky Way if the
Galactic bar is old.
,
suggesting that the velocity
distributions know about the spiral arm induced average local twist of the
potential well relative to the bar major axis. While this is especially true
for the more regular low-H regions, the velocity distributions show no
significant phase shift at all in the hot orbit region. The reason is because
the hot orbits are more eccentric and therefore are sensitive to more inner
features of the potential. It should be noted that in N-body
simulations like the one presented here, spiral arms are particularly strong
during about 1 Gyr after the formation of the bar, so that the reported
effects of spiral arms are probably overestimates for the Milky Way if the
Galactic bar is old.
![\begin{figure}
\par\includegraphics[width=6.8cm]{MS1098f19.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg275.gif) |
Figure 19:
Comparison of the normalised Hamiltonian values of a random selection
of
|
| Open with DEXTER | |
A potentially important difference of 3D models with respect to 2D models
is that the effective potential a star experiences near corotation depends on
its distance from the Galactic plane (see Fig. 16c). This raises the
average value of the Jacobi integral required for the stars to cross the
corotation radius and thus renders such a crossing more difficult. For stars
on the Solar circle, the higher effective value of H12 is not compensated
by their departure from the Galactic plane or a w velocity component.
Indeed, in our average N-body model, the change of effective
potential near corotation when moving from z=0 to z=300 pc is
![]() (with
(with
![]() as defined in the caption of Fig. 17), while
this change at the OLR of the axisymmetrised potential is only 0.004, and
adding a vertical velocity of
as defined in the caption of Fig. 17), while
this change at the OLR of the axisymmetrised potential is only 0.004, and
adding a vertical velocity of
![]() only increases
only increases
![]() by 0.005. Hence 2D models certainly exaggerate
the traffic of stars on hot orbits travelling from one side of corotation to
the other.
by 0.005. Hence 2D models certainly exaggerate
the traffic of stars on hot orbits travelling from one side of corotation to
the other.
Finally, Fig. 19 shows how the value of the Hamiltonian is
conserved during the N-body simulation. The main result is that the
H-values at different times are much better related for bar particles than
for (the dynamically defined) disc and hot particles. In particular, bar
particles remain bar particles, but disc particles can easily transform into
hot particles and vice versa for
![]() ,
supporting the
presumption in Sect. 7 that spiral arms may induce exchanges
between regular and chaotic phase space regions in real galaxies. Near the
1/1 resonance, the disc particles also reveal a smaller scatter of their
past versus present H relation. The normalised Hamiltonian (as well as the
absolute non-rescaled Hamiltonian) increases on the average for the disc
particles, which may be understood by the fact that the contribution of the
term
,
supporting the
presumption in Sect. 7 that spiral arms may induce exchanges
between regular and chaotic phase space regions in real galaxies. Near the
1/1 resonance, the disc particles also reveal a smaller scatter of their
past versus present H relation. The normalised Hamiltonian (as well as the
absolute non-rescaled Hamiltonian) increases on the average for the disc
particles, which may be understood by the fact that the contribution of the
term
![]() to
to
![]() diminishes as the bar
rotates slower, and decreases for the bar particles, owing to the deepening
of the central potential well.
diminishes as the bar
rotates slower, and decreases for the bar particles, owing to the deepening
of the central potential well.
It would be interesting to investigate the evolution of the particle H-values in an N-body simulation with a bar rotating at a constant frequency, for example without including a live dark halo component, in order to disentangle the effects of the spiral arms from the effects of a decreasing pattern speed. It would be also worth to explore the diffusion of particles from regular to chaotic phase space regions and vice versa, starting with 2D N-body simulations in a first approach. One problem to be clarified is why the N-body velocity distributions look so similar to the test particle ones, despite the action of such a diffusion process. A detailed analysis of the orbital structure in 3D models remains to be done, and in particular of the properties of the vertical motion within regular and chaotic regions.
Before concluding, we now present a selection of test particle and N-body velocity distributions yielding a good match to the observed one, confront the quasi-x1(2) orbit and chaotic orbit interpretations of the Hercules stream, paying also attention to the case of the Hyades stream, and discuss how the models could be further improved.
Beside the parameters in the initial conditions of the simulations, the
free model parameters are
![]() ,
,
![]() ,
the
velocity scale specified by
,
the
velocity scale specified by ![]() (defined as the local circular
velocity in the axisymmetric part
(defined as the local circular
velocity in the axisymmetric part
![]() of the potential for the
N-body simulation), which should lie between 180 and
230 kms-1 (e.g. Sackett 1997), and the velocity of the Sun
of the potential for the
N-body simulation), which should lie between 180 and
230 kms-1 (e.g. Sackett 1997), and the velocity of the Sun
![]() relative to the circular orbit in
relative to the circular orbit in
![]() .
A commonly adopted velocity reference in the Solar neighbourhood is the LSR,
defined as the velocity of the most nearly circular closed orbit passing
through the present location of the Sun according to Binney & Merrifield
(1998). This definition, which is merely an attempt to generalise the
circular LSR orbit of the axisymmetric case to non-axisymmetric potentials, is
not always well adapted. The most reasonable LSR orbit candidates near the OLR
of a barred potential indeed are the stable low-eccentricity x1(1) and
x1(2) orbits, but some space positions near the OLR circle are visited by
neither of these orbits in our models (see for example
.
A commonly adopted velocity reference in the Solar neighbourhood is the LSR,
defined as the velocity of the most nearly circular closed orbit passing
through the present location of the Sun according to Binney & Merrifield
(1998). This definition, which is merely an attempt to generalise the
circular LSR orbit of the axisymmetric case to non-axisymmetric potentials, is
not always well adapted. The most reasonable LSR orbit candidates near the OLR
of a barred potential indeed are the stable low-eccentricity x1(1) and
x1(2) orbits, but some space positions near the OLR circle are visited by
neither of these orbits in our models (see for example
![]() and
and
![]() in
Fig. 12). However, for
in
Fig. 12). However, for
![]() ,
there
always exists a prominent peak of low-eccentricity quasi-x1(1)
orbits in the model velocity distributions, which, as pointed out in
Sect. 7, not necessarily coincides with the trace of the
non-resonant x1(1) orbit when there is one. The maximum of this peak will
therefore be taken as the model "LSR'' and will be preferably associated to
the Coma Berenices stream, which is the local maximum in the observed velocity
distribution that lies closest to the heliocentric velocity of the LSR
,
there
always exists a prominent peak of low-eccentricity quasi-x1(1)
orbits in the model velocity distributions, which, as pointed out in
Sect. 7, not necessarily coincides with the trace of the
non-resonant x1(1) orbit when there is one. The maximum of this peak will
therefore be taken as the model "LSR'' and will be preferably associated to
the Coma Berenices stream, which is the local maximum in the observed velocity
distribution that lies closest to the heliocentric velocity of the LSR
![]() kms-1 derived from the Hipparcos data
(Dehnen & Binney 1998).
kms-1 derived from the Hipparcos data
(Dehnen & Binney 1998).
For
![]() ,
the quasi-x1(1) peak
is always close to the circular orbit of the axisymmetrised potential, except
near the OLR radius and
,
the quasi-x1(1) peak
is always close to the circular orbit of the axisymmetrised potential, except
near the OLR radius and
![]() where it reaches a maximum
positive v-offset of
where it reaches a maximum
positive v-offset of
![]() for all explored bar strengths.
Under the above circumstances and for realistic space positions, the azimuthal
velocity of the Sun should exceed the circular velocity by
5-10 kms-1.
for all explored bar strengths.
Under the above circumstances and for realistic space positions, the azimuthal
velocity of the Sun should exceed the circular velocity by
5-10 kms-1.
![\begin{figure}
\par\includegraphics[width=13cm]{MS1098f20.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg285.gif) |
Figure 20:
Selection of scaled velocity distributions from the test particle
(frame a) to d)) and N-body (frame e)) simulations,
with the various parameters indicated on the top of the frames and the
velocity origin at the adopted Solar motion. The velocity window and the
velocity contours are the same as in Fig. 1. The filled circles
represent the mean velocities of the streams listed in Table 1,
excluding the Arcturus stream. All distributions from the test particle
simulations are time averages over
|
| Open with DEXTER | |
The selected model velocity distributions are displayed in Fig. 20. The distributions are derived according to the same procedures as described in Sects. 7 and 10. Frame (a) shows a case where the Hercules-like stream is induced exclusively by chaotic orbits and peaks inside the H12 contour, illustrating the fact that chaotic modes not necessarily only occur in the hot orbit region. Here the Hyades stream coincides with a chaotic overdensity associated with a narrow and low-H chaotic breach roughly along the OLR curve, i.e. an interpretation similar to the one proposed in Sect. 7 for the u<0 extension of the LSR mode. Frame (c) gives a case where the Hercules-like stream now falls entirely in the hot orbit region and where the Hyades stream has the same chaotic origin as in frame (a).
Frame (e), derived from the N-body simulation and presenting a
larger velocity dispersion, provides a remarkable example of a Hercules-like
stream sustained exclusively by quasi-x1(2) orbits. The test
particle simulations develop quasi-x1(2) modes which cannot be as
easily matched to the Hercules stream in our scaling procedure, generally
falling right between this stream and the Hyades stream. This can be explained
by the different local slope of the circular velocity ![]() in the
N-body and the test particle models. As explained by D2000 in terms
of orbital frequencies, the separation between the quasi-x1(1) and
the quasi-x1(2) modes increases with
in the
N-body and the test particle models. As explained by D2000 in terms
of orbital frequencies, the separation between the quasi-x1(1) and
the quasi-x1(2) modes increases with
![]() .
Since the average N-body model has a slightly raising rotation curve
near the OLR radius (Fig. 16d), its circular velocity gradient is
larger than for the flat rotation curve test particle simulations and thus the
quasi-x1(2) mode is found at higher asymmetric drift relative to the
quasi-x1(1) mode. However, the fact that observations support a
rather gently declining rotation curve at
.
Since the average N-body model has a slightly raising rotation curve
near the OLR radius (Fig. 16d), its circular velocity gradient is
larger than for the flat rotation curve test particle simulations and thus the
quasi-x1(2) mode is found at higher asymmetric drift relative to the
quasi-x1(1) mode. However, the fact that observations support a
rather gently declining rotation curve at ![]() and that a large
inclination angle of the bar is needed (
and that a large
inclination angle of the bar is needed (
![]() for
for
![]() )
are arguments against the
quasi-x1(2) interpretation of the Hercules stream. On the other
hand, the displacement of the quasi-x1(2) peak towards the H12contour with increasing integration time mentioned in Sect. 7 for
F=0.10 and
)
are arguments against the
quasi-x1(2) interpretation of the Hercules stream. On the other
hand, the displacement of the quasi-x1(2) peak towards the H12contour with increasing integration time mentioned in Sect. 7 for
F=0.10 and
![]() may reinforce this
interpretation.
may reinforce this
interpretation.
Frame (d) is an example with two distinct low angular momentum peaks, the
most negative v one being related to chaotic hot orbits and the other one to
quasi-x1(2) orbits. It would be interesting to check whether a
sufficiently negative
![]() is able to shift
the quasi-x1(2) mode more towards the true location of the Hyades
stream and thus yield a model velocity distribution with a better overall
match to the observed one. Note that the chaotic orbit mode will not
necessarily be shifted as the quasi-x1(2) mode, because its location
in the u-v plane does not actually depend on the local slope of the circular
velocity, but rather on the difference of
is able to shift
the quasi-x1(2) mode more towards the true location of the Hyades
stream and thus yield a model velocity distribution with a better overall
match to the observed one. Note that the chaotic orbit mode will not
necessarily be shifted as the quasi-x1(2) mode, because its location
in the u-v plane does not actually depend on the local slope of the circular
velocity, but rather on the difference of
![]() between the current
space position and the Lagrangian point L1/2, which determines the u-vlocation of the H12 contour
between the current
space position and the Lagrangian point L1/2, which determines the u-vlocation of the H12 contour![]() . Finally, frame (b) displays a surprising case
where the velocity distribution in the quasi-x1(2) region of the
u-v plane (see Fig. 9) seems to have split into two peaks
coinciding well with the locations of the Hercules and Hyades streams, i.e.
both these streams have a quasi-x1(2) origin. However, this is
likely to be a transitory situation resulting from the unachieved phase mixing
near
. Finally, frame (b) displays a surprising case
where the velocity distribution in the quasi-x1(2) region of the
u-v plane (see Fig. 9) seems to have split into two peaks
coinciding well with the locations of the Hercules and Hyades streams, i.e.
both these streams have a quasi-x1(2) origin. However, this is
likely to be a transitory situation resulting from the unachieved phase mixing
near
![]() (see Sect. 7).
(see Sect. 7).
These examples illustrate the variety of possible interpretations for the Hercules and Hyades streams, and it is very hard at this stage to decide with certainty which one is the most appropriate. The splitting of the LSR mode into the Pleiades, Coma Berenices, Sirius and other streams is probably not related to the bar itself and has a more local origin, like for instance the effect of time dependent spiral arms.
The Galactic bar induces a characteristic splitting of the disc phase space into regular and chaotic orbit regions, with the latter regions owing only to the non-axisymmetric part of the potential in the limit of no vertical motion. In this paper, we have isolated these two kind of regions, as well as the quasi-periodic orbit sub-regions inside the regular regions associated with the stable x1(1) and x1(2) periodic orbits respectively, within the same analytical 2D rotating barred potential with flat azimuthally averaged rotation curve as in D2000. We then have run test particle simulations in this potential and a more realistic self-consistent 3D N-body simulation to find out how the disc distribution function outside the bar region relates to such a phase space splitting and in particular how chaos may explain features in the Solar neighbourhood stellar kinematics like the Hercules stream.
Beside the bar strength, the regular versus chaotic splitting of phase
space, investigated via the largest Liapunov exponent, is mainly determined by
the value of the Hamiltonian H (or Jacobi's integral) and by the bar related
resonances. In two dimensions and at fixed space position, the constant-Hcontours in the galactocentric u-v velocity plane are circles centred on
![]() and of radius
and of radius
![]() ,
where
,
where ![]() is the galactocentric
distance,
is the galactocentric
distance,
![]() the rotation frequency of the bar and
the rotation frequency of the bar and
![]() the local effective potential. The fraction of
chaotic orbits increases with H and there is a sharp average transition from
regular to chaotic behaviour in the u-v plane when crossing the contour
corresponding to the effective potential at the saddle Lagrangian points,
the local effective potential. The fraction of
chaotic orbits increases with H and there is a sharp average transition from
regular to chaotic behaviour in the u-v plane when crossing the contour
corresponding to the effective potential at the saddle Lagrangian points,
![]() ,
which generally intersects the
v-axis at lower velocity than the circular orbit in the axisymmetric
part of the potential. At H<H12, the orbits are rather regular, while at
H>H12, which defines the category of hot orbits susceptible to
cross the corotation radius, they are rather chaotic.
,
which generally intersects the
v-axis at lower velocity than the circular orbit in the axisymmetric
part of the potential. At H<H12, the orbits are rather regular, while at
H>H12, which defines the category of hot orbits susceptible to
cross the corotation radius, they are rather chaotic.
The resonances, on the other hand, generate an alternation of regular and
chaotic orbit arcs in the velocity plane which, contrary to the low-v part
of the H-contours, are opened towards lower angular momentum. At bar
inclination angles ![]() and
and
![]() ,
the maxima or minima
of these stochasticity waves are in phase with the resonance curves derived
from the axisymmetric limit and the arcs are symmetric in u, reflecting the
four-fold symmetry of the potential. At intermediate angles, these extrema
become offset with respect to the resonance curves and the u-symmetry
breaks. In particular, at
,
the maxima or minima
of these stochasticity waves are in phase with the resonance curves derived
from the axisymmetric limit and the arcs are symmetric in u, reflecting the
four-fold symmetry of the potential. At intermediate angles, these extrema
become offset with respect to the resonance curves and the u-symmetry
breaks. In particular, at
![]() and
and
![]() ,
a prominent regular region of eccentric
quasi-x1(1) orbits extends well within the hot orbit region at
,
a prominent regular region of eccentric
quasi-x1(1) orbits extends well within the hot orbit region at
![]() ,
while the u>0 counterpart of the OLR curve is surrounded by a wide
chaotic region consistent with the location of the Hercules stream.
,
while the u>0 counterpart of the OLR curve is surrounded by a wide
chaotic region consistent with the location of the Hercules stream.
For a moderate bar strength (F=0.10), the low-eccentricity and
non-resonant quasi-x1(2) orbit regions exist only for
![]() and over an angle range around
and over an angle range around
![]() increasing towards smaller R. There is no such region
near the default position considered in D2000, i.e.
increasing towards smaller R. There is no such region
near the default position considered in D2000, i.e.
![]() and
and
![]() ,
compromising
the quasi-x1(2) orbit interpretation given by Dehnen for the
Hercules-like mode occuring in his simulations at the most realistic positions
of the Sun relative to the bar.
,
compromising
the quasi-x1(2) orbit interpretation given by Dehnen for the
Hercules-like mode occuring in his simulations at the most realistic positions
of the Sun relative to the bar.
The test particle simulations, started from axisymmetric initial
conditions and progressively exposed to the full rotating barred potential,
reveal a decoupled evolution of the disc distribution function within the
regular and chaotic phase space regions. In the regular regions, the phase
space density after phase mixing is roughly the same as the initial one,
whereas in the chaotic regions, the particles quickly evolve towards a uniform
population of the easily available phase space volume via chaotic mixing,
resulting in a substantial density re-adjustment. Because the space region
within corotation represents a large initial reservoir of hot chaotic orbit
particles which are spread throughout the disc by this process, yielding a net
outward migration of such particles, the chaotic regions in the u-v plane
outside corotation become more heavily crowded than the regular regions at
![]() .
In particular, the wide and predominantly u>0 chaotic region
mentioned above for realistic space positions of the Sun appears as an
overdensity in the u-v distribution, providing a coherent interpretation of
the Hercules stream and explaining the u>0 property of this stream.
According to this interpretation, the Hercules stream involves stars on
essentially chaotic orbits which are forced to avoid the regular x1(1)region at negative u.
.
In particular, the wide and predominantly u>0 chaotic region
mentioned above for realistic space positions of the Sun appears as an
overdensity in the u-v distribution, providing a coherent interpretation of
the Hercules stream and explaining the u>0 property of this stream.
According to this interpretation, the Hercules stream involves stars on
essentially chaotic orbits which are forced to avoid the regular x1(1)region at negative u.
The time averaged disc u-v velocity distributions inferred from the N-body simulation are remarkably similar to those of the test particle simulations, despite the action of the transient spiral arms which allows at least some of the particles to diffuse from the regular to the chaotic regions and vice versa. At low eccentricity, the orbits are less sensitive to the inner features of the potential and the azimuthal properties of the velocity distributions essentially align with the average local phase shift of the potential well relative to the bar major axis induced by the spiral arms.
The velocity distributions may be very time dependent if for
instance the bar has formed recently, because of the phase mixing occuring
in the disc during at least ![]() 10 bar rotations after the growth of the
bar according to the test particle simulations. The u-v distributions in the
N-body simulation at fixed space position relative to the bar also
display a strong temporal behaviour (see the mpeg movies at
http://www.mso.anu.edu.au/~fux/streams.html), as expected from the
presence of the transient spiral waves. However, since the simulation has been
run for only about 1.25 Gyr after the formation of the bar, phase mixing
is still operating in the disc component, rendering difficult to disentangle
from it the individual effects of such waves. The N-body simulation also
gives some insight on the consequences of evolving bar parameters: the slowly
decreasing pattern speed of the bar mainly introduces a delayed response of
the disc distribution function to the outward moving resonances, so that the
velocity distributions at a given time rather reflect a higher value of
10 bar rotations after the growth of the
bar according to the test particle simulations. The u-v distributions in the
N-body simulation at fixed space position relative to the bar also
display a strong temporal behaviour (see the mpeg movies at
http://www.mso.anu.edu.au/~fux/streams.html), as expected from the
presence of the transient spiral waves. However, since the simulation has been
run for only about 1.25 Gyr after the formation of the bar, phase mixing
is still operating in the disc component, rendering difficult to disentangle
from it the individual effects of such waves. The N-body simulation also
gives some insight on the consequences of evolving bar parameters: the slowly
decreasing pattern speed of the bar mainly introduces a delayed response of
the disc distribution function to the outward moving resonances, so that the
velocity distributions at a given time rather reflect a higher value of
![]() than the true instantaneous one when compared with
the constant
than the true instantaneous one when compared with
the constant
![]() test particle simulations. For completeness, one
should mention that other perturbations than the bar and the spiral arms may
provide alternative explanations of the local stellar streams, like for
example the interactions of the Milky Way with its satellite companions.
test particle simulations. For completeness, one
should mention that other perturbations than the bar and the spiral arms may
provide alternative explanations of the local stellar streams, like for
example the interactions of the Milky Way with its satellite companions.
Finally, the process of chaotic mixing, combined with the possible stellar exchanges between the regular and chaotic phase space regions resulting from the diffusion of stars by transient spiral arms or molecular clouds, may provide an new and efficient way of heating galactic discs which remains to be explored.
Acknowledgements
I would like to thank K.C. Freeman for a careful reading of the manuscript and A. Kalnajs for many enriching interactions. I am also thankful to Walter Dehnen for having partly inspired the present investigation and for several enlightening discussions, and to the University of Geneva where the N-body simulation presented in Sect. 10 has been performed. This work was mainly supported by the Swiss National Science Foundation.