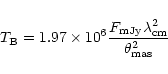Up: The radio corona of
4 Discussion
The availability of both microwave spectra and spatial information
at the same time gives us the opportunity to model the coronae of AR Lac.
As shown in previous papers (Umana et al. 1993; Umana et al.
1999), the observed flat radio spectra of Algols and RS CVn type
binary systems cannot be reproduced by an homogeneous source model.
VLBI observations of the close binary systems Algol and UX Arietis pointed out
the existence of a two component structure in the coronal layers (Mutel et al.
1985; Lestrade et al. 1998):
a compact core, coinciding with the active star, and a larger halo, having
approximatively the size of the entire system.
We used the core-halo model developed by Umana et al. (1993) to fit
the observed spectra of AR Lac, in order to check if the flux
variability can be attributed to the variation of one of the
parameters.
Although it is not possible to derive a unique solution, we have limited the
sizes of core and halo on the basis of the VLBA observation results.
In particular, for the halo we assumed the size measured from the VLBA data,
and for the core a size smaller than the resolution limit of the
interferometer.
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{ms10553f5.eps} \end{figure}](/articles/aa/full/2001/25/aa10553/Timg38.gif) |
Figure 5:
Comparison between the observed radio spectra of AR Lac
shown in Fig. 2
and the computed spectra obtained by assuming a core-halo structure for the
radio source (thick line). The contribution of the halo (dot-dashed line)
and core (dashed line) to the composite spectrum are also shown. |
For the magnetic field strength we assumed
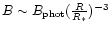 ,
where
,
where
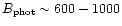 Gauss, as derived
for other RS CVn systems (Gondoin et al. 1985; Donati et al.
1992).
Gauss, as derived
for other RS CVn systems (Gondoin et al. 1985; Donati et al.
1992).
According to these constraints, we derived the best core-halo model fit
labeled a in Fig. 2. We then
used the derived values of the average magnetic field strength Band energetic electron number density (
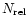 ),
in fitting the other 5 spectra,
under the hypothesis that these physical properties of
the coronal emitting regions are stationary.
Then we tried to fit the other spectra by varying only the structure size.
The results of our analysis are summarised in Table 3 and are shown in
Fig. 5. For the spectra from a to d, we can get a good
agreement between the observed data
and a core-halo structure by assuming that the flux variations are due to
structure size changes in the range of 1.1 and 1.4 times the stellar
radius, corresponding a variation of 0.3 mas, which is below
the errors of our measurements.
),
in fitting the other 5 spectra,
under the hypothesis that these physical properties of
the coronal emitting regions are stationary.
Then we tried to fit the other spectra by varying only the structure size.
The results of our analysis are summarised in Table 3 and are shown in
Fig. 5. For the spectra from a to d, we can get a good
agreement between the observed data
and a core-halo structure by assuming that the flux variations are due to
structure size changes in the range of 1.1 and 1.4 times the stellar
radius, corresponding a variation of 0.3 mas, which is below
the errors of our measurements.
The low s/n ratio of the VLBA data does not permit us
to investigate the behaviour of the emitting region size for each single scan,
and so as a function of the orbital phase.
The source size is very close to the beam width, so it was not
possible to obtain an estimate of the source size for the time ranges
during which the flux density was lower then  2 mJy.
Nevertheless, the results obtained
for the scans with sufficient s/n ratio, that are shown in Fig. 6
by diamond symbols,
suggest that the source size remains almost constant, as the measured
changes fall within errors.
2 mJy.
Nevertheless, the results obtained
for the scans with sufficient s/n ratio, that are shown in Fig. 6
by diamond symbols,
suggest that the source size remains almost constant, as the measured
changes fall within errors.
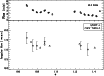 |
Figure 6:
Lower panel: source size estimates as a function of orbital phase.
The diamonds represent the value obtained from UVFIT, the triangles represent
the value of source size we used to fit the observed spectra with the core-halo
model.
Upper panel: the corresponding total flux density at 8.4 GHz. |
On the other hand, it should be noted that the
slow modulation of the modelled halo size is in good agreement with
the results obtained from an independent analysis of
the VLBA data and plotted in Fig. 6.
To fit the spectra e and h, we had to assume an "ageing''
of the relativistic electron population and a variation of its number
density from
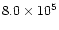 to
to
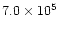 cm-3, that is
needed to explain the faster decay at the higher frequency.
cm-3, that is
needed to explain the faster decay at the higher frequency.
If the core-halo model is able to account for the radio corona of
AR Lac, the visibilities of the VLBA data should fit by a
two Gaussian model corresponding to the core and halo.
For the Nov. 2-3 data, the average size of the core from the analysis of
the spectra a, b, c, d is 0.15 mas, and the average flux density
at 8.4 GHz is 1.21 mJy; for the halo, 1.25 mas and 1.74 mJy.
For the Nov. 3-4 data, the same parameters from the analysis of the spectra
e and f are 0.145 mas, 1.05 mJy for the core and 1.20 mas,
1.17 mJy for the halo.
We then model the normalized visibility function at 8.4 GHz with that
corresponding to
the core-halo model (Fig. 4). It is evident
that the VLBA data are consistent with the core-halo scenario
derived from the analysis of the radio spectra.
VLBA data indicate a source size close to the
separation of the binary components,
suggesting the possibility of an emitting region located between
the system components.
UV emission from plasma close to the Lagrangian point in between the system
components
has been suggested
for AR Lac (Pagano et al.
2001) and other RS CVn-type systems (Busà et al. 1999).
In partial overlap to our observations, X-ray observations of AR Lac
were performed with the Beppo SAX satellite (Rodonò et al. 1999).
This gave us the opportunity to
determine whether
the physical parameters of the
radio emitting regions, derived from the comparisons between the observations
and the core-halo models, are consistent with a co-spatial model for both the
X-ray and radio emitting source.
Spectral analyses performed by several authors (Swank et al. 1981;
Singh et al. 1995)
showed that the X-ray emission from close binary systems requires
at least two plasma components characterised by different temperature and
volumetric emission measures (EM) to be modelled.
On the basis of the first observation run, that started on Nov. 2 at 06:07 and ended
on Nov. 4 at 17:50, Rodonò et al. (1999) derived for the first
component
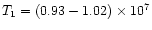 K and
K and
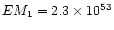 cm-3
and for the second
cm-3
and for the second
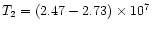 K and
K and
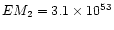 cm-3.
cm-3.
Assuming that the higher temperature component is associated with the halo and
the the lower temperature component with the core, we can check if the magnetic
field, as derived from the radio data, is strong enough to contain the
X-ray source. This means that 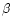 ,
i.e. the ratio between the density
of kinetic energy (
,
i.e. the ratio between the density
of kinetic energy (
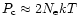 )
and the density of
magnetic energy (
)
and the density of
magnetic energy (
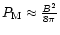 )
has to be less then
unity.
If the plasma density
)
has to be less then
unity.
If the plasma density 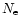 is constant over the emitting volume
V,
is constant over the emitting volume
V,
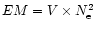 ,
and assuming the size (radius) from the
analysis of the radio data of
,
and assuming the size (radius) from the
analysis of the radio data of
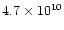 and
and
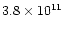 cm
for the core and the halo respectively, we get
cm
for the core and the halo respectively, we get
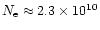 and
and
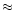
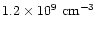 (see Table 3).
(see Table 3).
We obtain
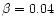 for the core and
for the core and
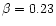 for the halo. The
physical parameters obtained from our analysis are therefore consistent with
the hypothesis of a co-spatial X-ray and radio source.
for the halo. The
physical parameters obtained from our analysis are therefore consistent with
the hypothesis of a co-spatial X-ray and radio source.
We will furthermore test the possibility that the radio emission can be
attributed to the same thermal electron population responsible for the observed
X-ray emission.
The brightness temperature of the resolved radio source at 3.6 cm, obtained
from the relation
is
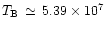 K
and
K
and
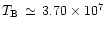 K
for the first and the second session, respectively. These values are higher by
a factor of two than the temperature derived from the Beppo SAX data,
but the order of magnitude is the same.
We simulated
the spectra
of a core-halo structure by adopting thermal gyrosynchrotron emission and
using the expression given by Dulk (1985) for the emission and
absorption coefficients. By combining the physical parameters
derived from Rodonò et al. (1999) for the thermal coronal plasma
with our VLBA results, we can fix
the temperature, the thermal plasma
density and the maximum size of the emitting regions. The only free
parameter left is, thus, the magnetic field strength. The spectrum obtained
for B=600 Gauss for the core and B=200 Gauss for the halo is plotted
in Fig. 7 and compared with the spectra obtained from the
VLA maps over the two sessions.
K
for the first and the second session, respectively. These values are higher by
a factor of two than the temperature derived from the Beppo SAX data,
but the order of magnitude is the same.
We simulated
the spectra
of a core-halo structure by adopting thermal gyrosynchrotron emission and
using the expression given by Dulk (1985) for the emission and
absorption coefficients. By combining the physical parameters
derived from Rodonò et al. (1999) for the thermal coronal plasma
with our VLBA results, we can fix
the temperature, the thermal plasma
density and the maximum size of the emitting regions. The only free
parameter left is, thus, the magnetic field strength. The spectrum obtained
for B=600 Gauss for the core and B=200 Gauss for the halo is plotted
in Fig. 7 and compared with the spectra obtained from the
VLA maps over the two sessions.
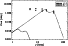 |
Figure 7:
Simulated spectra from a core-halo structure for thermal
gyrosynchrotron obtained with a magnetic field of 600 Gauss in the core and
200 Gauss in the halo (thick line) and  Gauss in the core and
300 Gauss (dashed line) for the halo.
Overlaid are the average spectra for the two sessions.
Gauss in the core and
300 Gauss (dashed line) for the halo.
Overlaid are the average spectra for the two sessions. |
It is evident that gyrosynchrotron emission from the same thermal population
responsible for the X-ray emission is not able to account for the observed
spectra, unless magnetic field strengths higher then 1000 Gauss are considered.
Moreover, even assuming such an intense magnetic field, it is not possible to
reproduce the quite flat observed spectra.
Beasley & Guedel (2000) reached a similar result from
simultaneous radio and X-ray observations of the RS CVn-type
binary system UX Ari during quiescence.


Up: The radio corona of
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{ms10553f5.eps} \end{figure}](/articles/aa/full/2001/25/aa10553/Timg38.gif)