

Up: The radio corona of
Subsections
In order to investigate the temporal radio flux behaviour of the source
and locate possible rapid flux variations, we analysed each scan with the
AIPS program DFTPL. This procedure performs the direct Fourier transform of the
visibility function in a limited portion of the UV plane. The results of such an
analysis led to the conclusion that, even if the radio flux of AR Lac
is variable, it does not change significantly on timescales shorter than 45 min, which is about the time length of each scan.
In Fig. 1 the flux curves, obtained by averaged flux in 20 min bins
and using the new ephemeris by Marino et al. (1998), are shown.
The source was detected at all frequencies during both sessions,
except during the last session in the Q-band, where only an upper limit of
0.6 mJy for the flux density can be given. This value corresponds
to the rms of the cleaned map integrated over the entire 14 hours.
A clear flux variation, more evident at the lowest
frequencies (up to a factor of 2 in C-band), seems
to indicate the presence of inhomogeneous features on one or
both of the system's components.
Unfortunately, AR Lac was not visible from the VLA during eclipses.
We observed a clear flux maximum at phase 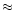 0.88, and a clear decay at
the beginning of each of the two sessions, suggesting a flux modulation versus
phase.
No significant circular polarization at any observed frequency was detected.
0.88, and a clear decay at
the beginning of each of the two sessions, suggesting a flux modulation versus
phase.
No significant circular polarization at any observed frequency was detected.
Since each band was not observed continuously, it is not possible
to build radio spectra with simultaneous flux measurements at all the
frequencies. However, the variations of the flux are slow, and it was possible
to make reasonable interpolations in order to obtain the radio spectra.
Six spectra corresponding to
different times are shown in Fig. 2. They all show negative
spectral indexes 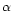 (
(
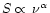 ),
implying that the source is optically thin in the available
range of frequencies
(
),
implying that the source is optically thin in the available
range of frequencies
(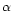 varies from -0.16 to -0.45).
There is no evidence of a turn-over frequency,
which is presumable lower than 5 GHz.
The spectra show approximately the same shape, and the main difference
is variation in flux density.
varies from -0.16 to -0.45).
There is no evidence of a turn-over frequency,
which is presumable lower than 5 GHz.
The spectra show approximately the same shape, and the main difference
is variation in flux density.
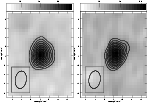 |
Figure 3:
VLBA maps of AR Lac at 8.4 GHz for Nov. 2-3 (left) and Nov. 3-4 (right).
The rms of both maps is 0.06 mJy/beam and the peak intensity are 1.26 and
1.07 mJy, respectively. For the first map the contours correspond to
0.25, 0.38, 0.50, 0.63, 0.76, 0.88, 1. 01, 1.13, 1.21 mJy,
for the second map correspond to
0, 0.21, 0.32, 0.43, 0.54, 0.64, 0.75, 0.86, 0.96, 1.03 mJy.
On the lower left corner the restoring beam is shown. |
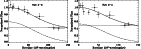 |
Figure 4:
Correlated flux at 3.6 cm on the VLA-VLBA baselines as function of u-v
distance, for Nov. 2-3 and Nov. 3-4.
The lines represent the visibility of the core-halo model (continuous lines),
of the single core (dot lines) and halo (dashed lines) as discussed in
Sect. 4. |
In Fig. 3 the VLBA cleaned map of AR Lac for the two sessions,
which were obtained from the phase reference calibration, are shown.
The FWHMs of the beam for both the maps are
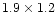 mas, with a position angle of
mas, with a position angle of
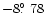 and
and
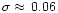 mJy. We did not measure significant circular
polarisation from the VLBA data.
The source appears resolved and the two maps do not show significant changes
in their structure.
The evidence of a resolved structure is confirmed by the analysis of the visibility
amplitude versus the projected baseline spacing for the VLBA
baselines involving VLA, which is shown in Fig. 4.
The correlated flux has been first coherently averaged through the scan and
then the amplitudes normalized to the zero spacing value, which was
assumed to be equal to the total flux obtained from the VLA measurements in
the same scan.
Then, the visibility amplitudes have been averaged for each baseline,
whose length variation during the observation is indicated by the horizontal
bars.
In order to measure the size of the emitting regions, or to derive the upper
limit, we fitted the data with a two dimensional Gaussian model by using the
AIPS routines UVFIT and JMFIT.
The first routine gives an acceptable fit of UV-data with an elliptical
Gaussian with
FWHM of
mJy. We did not measure significant circular
polarisation from the VLBA data.
The source appears resolved and the two maps do not show significant changes
in their structure.
The evidence of a resolved structure is confirmed by the analysis of the visibility
amplitude versus the projected baseline spacing for the VLBA
baselines involving VLA, which is shown in Fig. 4.
The correlated flux has been first coherently averaged through the scan and
then the amplitudes normalized to the zero spacing value, which was
assumed to be equal to the total flux obtained from the VLA measurements in
the same scan.
Then, the visibility amplitudes have been averaged for each baseline,
whose length variation during the observation is indicated by the horizontal
bars.
In order to measure the size of the emitting regions, or to derive the upper
limit, we fitted the data with a two dimensional Gaussian model by using the
AIPS routines UVFIT and JMFIT.
The first routine gives an acceptable fit of UV-data with an elliptical
Gaussian with
FWHM of
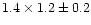 mas, while the second one
fits the source image with a Gaussian component having FWHM of
mas, while the second one
fits the source image with a Gaussian component having FWHM of
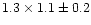 mas. The two models are then consistent with
each other and with a circular symmetric source.
Using a circular Gaussian to fit the data, we obtain a source size of
mas. The two models are then consistent with
each other and with a circular symmetric source.
Using a circular Gaussian to fit the data, we obtain a source size of
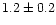 mas,
corresponding to
mas,
corresponding to
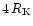 (see Table 1) or 1.2 times
the system separation (
(see Table 1) or 1.2 times
the system separation (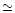 1 mas).
Our data are also compatible with two component models, where the
first component is resolved, with a dimension between 1.3 and 1.6 mas,
while the second component is a point source. On the basis of
1 mas).
Our data are also compatible with two component models, where the
first component is resolved, with a dimension between 1.3 and 1.6 mas,
while the second component is a point source. On the basis of 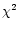 results
we cannot exclude the presence of such a compact core.
results
we cannot exclude the presence of such a compact core.


Up: The radio corona of
Copyright ESO 2001
![]() 0.88, and a clear decay at
the beginning of each of the two sessions, suggesting a flux modulation versus
phase.
No significant circular polarization at any observed frequency was detected.
0.88, and a clear decay at
the beginning of each of the two sessions, suggesting a flux modulation versus
phase.
No significant circular polarization at any observed frequency was detected.
![]() (
(
![]() ),
implying that the source is optically thin in the available
range of frequencies
(
),
implying that the source is optically thin in the available
range of frequencies
(![]() varies from -0.16 to -0.45).
There is no evidence of a turn-over frequency,
which is presumable lower than 5 GHz.
The spectra show approximately the same shape, and the main difference
is variation in flux density.
varies from -0.16 to -0.45).
There is no evidence of a turn-over frequency,
which is presumable lower than 5 GHz.
The spectra show approximately the same shape, and the main difference
is variation in flux density.