To first order, the AIB profiles essentially remain identical
while the exciting radiation hardens considerably:
![]() 000 K in NGC 2023 to
45000 K in M17-SW corresponding to the mean energy of the photons absorbed by a PAH
of 6 and 9 eV respectively. Such contrasted internal energies
imply differences in the emission temperature of a few 100 K for a given molecular size.
With this temperature change, band position shifts and band broadening of at least 10 cm_1 are expected
(Joblin et al. 1995). How can then the interstellar AIB profiles be so stable? One possibility
is that some process keeps the temperature distribution of interstellar PAHs essentially
the same.
000 K in NGC 2023 to
45000 K in M17-SW corresponding to the mean energy of the photons absorbed by a PAH
of 6 and 9 eV respectively. Such contrasted internal energies
imply differences in the emission temperature of a few 100 K for a given molecular size.
With this temperature change, band position shifts and band broadening of at least 10 cm_1 are expected
(Joblin et al. 1995). How can then the interstellar AIB profiles be so stable? One possibility
is that some process keeps the temperature distribution of interstellar PAHs essentially
the same.
To investigate this issue, we have computed the temperature distribution and
associated infrared (IR) emission of an interstellar PAH population using a modified version of the model
described in Pech et al. (2000 hereafter PJB) where we study in detail the temperature fluctuations and the
temperature distribution of PAHs. Improving on former work (Léger et al. 1989b; Schutte et al. 1993;
Cook & Saykally 1998), this model takes
into account the full spectral distribution of the exciting radiation and implements the recent results of Joblin
et al. (1995) on the temperature dependence of the band profiles of neutral PAHs.
In addition, it must be emphasized that the PAH IR emission cross-section of the PJB model was derived from
studies on PAH cations: indeed, we show in Sect. 4.4.1 that singly ionized PAHs
reproduce better the astronomical AIB spectra confirming previous work (Langhoff 1996; Cook & Saykally 1998;
Allamandola et al. 1999; Hudgins & Allamandola 1999). This observational requirement is supported by theoretical
studies on the charge state of interstellar PAHs for physical conditions comparable to those of our sample
of objects (Bakes & Tielens 1994; Dartois & d'Hendecourt 1997).
We first briefly describe the equations giving
the PAH cooling curve and emission, compute the temperature distribution of interstellar PAHs and then
compare our model PAH emission spectrum to the data. For the sake of clarity, we limit the model-to-data
comparison to NGC 2023 and M17-SW which are the extreme cases of our data sample and we focus on the well-defined
3.3, 6.2, 8.6 and 11.3 ![]() m-bands.
In order to emphasize the temperature fluctuations of PAHs
and the resulting temperature distribution, we have written the model equations in terms of cross-sections rather
than Einstein A-coefficients: this formulation is however strictly equivalent to that of PJB (see, e.g. ,
Schutte et al. 1993, Eq. (15)).
m-bands.
In order to emphasize the temperature fluctuations of PAHs
and the resulting temperature distribution, we have written the model equations in terms of cross-sections rather
than Einstein A-coefficients: this formulation is however strictly equivalent to that of PJB (see, e.g. ,
Schutte et al. 1993, Eq. (15)).
In the interstellar medium, a PAH containing ![]() carbon atoms absorbs radiation from the surrounding
stars at a rate:
carbon atoms absorbs radiation from the surrounding
stars at a rate:
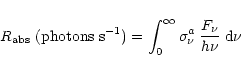 |
(1) |
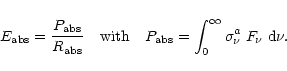 |
(2) |
As shown by Léger et al. (1989a) and Schutte et al. (1993), the IR emission of a
PAH is well treated within the thermal approximation and using
Kirchhoff's law. In the following, we will discuss the complete spectrum emitted by PAHs in terms of
the spectral energy distribution (SED) noted ![]() which is equal to
which is equal to
![]() .
The SED (in Watt) emitted by a single
molecule containing
.
The SED (in Watt) emitted by a single
molecule containing ![]() carbon atoms is thus:
carbon atoms is thus:
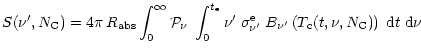 |
(3) |
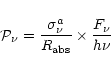 |
(4) |
The PAH IR emission cross-section is defined as in PJB. The band profiles have a Lorentzian shape
and at 3.3, 6.2, 8.6 and 11.3 ![]() m, the band position and width follow temperature dependent laws.
Each Lorentz profile is normalized to the peak value of the band cross-section,
m, the band position and width follow temperature dependent laws.
Each Lorentz profile is normalized to the peak value of the band cross-section,
![]() and
we assume that the integrated cross-section (or Einstein A-coefficient, see Schutte et al. 1993) of each band profile
is conserved with temperature. As already noted above, the resulting IR cross-section describes the properties of singly-ionized PAHs.
To match the observed AIB, the 8.6
and
we assume that the integrated cross-section (or Einstein A-coefficient, see Schutte et al. 1993) of each band profile
is conserved with temperature. As already noted above, the resulting IR cross-section describes the properties of singly-ionized PAHs.
To match the observed AIB, the 8.6 ![]() m-band had to be multiplied by 3. Because the available laboratory results do not account for the
complex shape of the observed 7.7
m-band had to be multiplied by 3. Because the available laboratory results do not account for the
complex shape of the observed 7.7 ![]() m-band (see Sect. 3), we define an empirical 7.7
m-band (see Sect. 3), we define an empirical 7.7 ![]() m-band with a shape derived from the
observations (profile centre at 1300 cm_1 and
m-band with a shape derived from the
observations (profile centre at 1300 cm_1 and
![]() cm_1 from the present data) and
with the (laboratory determined) Einstein A-coefficient of PJB. This profile of the 7.7
cm_1 from the present data) and
with the (laboratory determined) Einstein A-coefficient of PJB. This profile of the 7.7 ![]() m-band is furthermore assumed temperature
independent. We also added the 16.4
m-band is furthermore assumed temperature
independent. We also added the 16.4 ![]() m-AIB detected by ISO towards many sightlines (Moutou et al. 2000;
van Kerckhoven et al. 2000). This band is often
associated with the "classical'' 3 to 13
m-AIB detected by ISO towards many sightlines (Moutou et al. 2000;
van Kerckhoven et al. 2000). This band is often
associated with the "classical'' 3 to 13 ![]() m-AIBs and its intensity is not related to the hot dust
continuum appearing in more excited objects (see Fig. 1), i.e. , as for the other AIBs.
We represent the 16.4
m-AIBs and its intensity is not related to the hot dust
continuum appearing in more excited objects (see Fig. 1), i.e. , as for the other AIBs.
We represent the 16.4 ![]() m-band with a Lorentz profile centered at 609 cm_1, with
m-band with a Lorentz profile centered at 609 cm_1, with
![]() cm_1
(both being observational values, see Moutou et al. 2000) and an Einstein A-coefficient of
cm_1
(both being observational values, see Moutou et al. 2000) and an Einstein A-coefficient of
![]() s-1 per carbon atom
which corresponds to the average value of the laboratory measurements given in Moutou et al. (1996, Table 3).
As we will see below, the intensity of the 16.4
s-1 per carbon atom
which corresponds to the average value of the laboratory measurements given in Moutou et al. (1996, Table 3).
As we will see below, the intensity of the 16.4 ![]() m-band can constrain the power-law index of the PAH
size distribution. At longer wavelengths, we adopted the far-IR (
m-band can constrain the power-law index of the PAH
size distribution. At longer wavelengths, we adopted the far-IR (
![]()
![]() m) cross-section
of Schutte et al. (1993).
m) cross-section
of Schutte et al. (1993).
The size distribution of PAHs is defined by d
![]() ,
i.e., the number of PAHs with a
number of C-atoms between
,
i.e., the number of PAHs with a
number of C-atoms between ![]() and
and
![]() .
Writing the size distribution with respect to
.
Writing the size distribution with respect to ![]() frees us of
any assumptions on the PAH geometrical shape
frees us of
any assumptions on the PAH geometrical shape![]() . The number of H-atoms per
molecule is assumed to be
. The number of H-atoms per
molecule is assumed to be
![]() (Omont 1986, in the case of symmetric PAHs) with
(Omont 1986, in the case of symmetric PAHs) with ![]() the
hydrogenation fraction of a molecule: if
the
hydrogenation fraction of a molecule: if
![]() the molecule is completely dehydrogenated, if
the molecule is completely dehydrogenated, if
![]() the
molecule is fully hydrogenated. Unless otherwise stated, we will assume
the
molecule is fully hydrogenated. Unless otherwise stated, we will assume
![]() .
The mass distribution is then straightforwardly found as d
.
The mass distribution is then straightforwardly found as d
![]() where
where ![]() is the carbon atomic mass and
is the carbon atomic mass and ![]() the atomic mass of hydrogen. The
normalization factor, B, is determined from the PAH abundance in terms of the
fraction of interstellar carbon ([C/H]
the atomic mass of hydrogen. The
normalization factor, B, is determined from the PAH abundance in terms of the
fraction of interstellar carbon ([C/H]
![]() ,
Snow & Witt 1996) locked up
in PAHs. Finally, the emergent SED emitted by PAHs is
,
Snow & Witt 1996) locked up
in PAHs. Finally, the emergent SED emitted by PAHs is
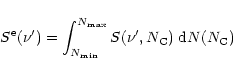 |
(5) |
Upon absorption of a UV-photon, the PAH temperature is raised to a peak value,
![]() .
The molecule then cools rapidly by the emission of IR vibrational mode photons.
The peak temperature
.
The molecule then cools rapidly by the emission of IR vibrational mode photons.
The peak temperature ![]() is found from first principles:
is found from first principles:
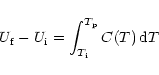 |
(6) |
The cooling curve
![]() is obtained by numerical integration (vs. temperature)
of the energy conservation relationship during cooling,
is obtained by numerical integration (vs. temperature)
of the energy conservation relationship during cooling,
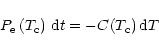 |
(7) |
The power emitted by a PAH at temperature T is:
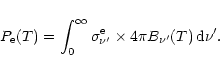 |
(8) |
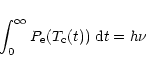 |
(9) |
Each molecule sees its cooling interrupted by the absorption of the next photon which
is a stochastic process (Désert et al. 1986). Moreover,
gas-grain exchanges must be taken into account (Rouan et al. 1992; Draine & Lazarian 1998)
to reliably estimate the temperature of a PAH in the low temperature part of the cooling curve.
In fact, the emission from
the cool (but long-lasting) tail of the cooling curves will peak in the far-IR/submillimeter, far away
from the 3 to 20 ![]() m-range on which we focus here. The
detailed treatment of this problem is outside the scope of this paper and we adopt the
following simple criterion to truncate our cooling curves.
The mean time elapsed between two photon absorptions is
m-range on which we focus here. The
detailed treatment of this problem is outside the scope of this paper and we adopt the
following simple criterion to truncate our cooling curves.
The mean time elapsed between two photon absorptions is
![]() :
it is for instance 6.9 and 2.6 hours
in the radiation field of NGC 2023 and M17-SW respectively and for a molecule with
:
it is for instance 6.9 and 2.6 hours
in the radiation field of NGC 2023 and M17-SW respectively and for a molecule with
![]() .
Consequently, all cooling curves have been truncated at
.
Consequently, all cooling curves have been truncated at
![]() to
account for the repeated absorptions of UV photons by a molecule;
to
account for the repeated absorptions of UV photons by a molecule; ![]() decreases as
decreases as
![]() because
because
![]() .
We thus define the lowest
temperature of a PAH heated by a photon of energy
.
We thus define the lowest
temperature of a PAH heated by a photon of energy ![]() as
as
![]() ,
i.e. , equal
to the temperature at the end of the cooling.
For instance, in the radiation field of NGC 2023 small PAHs
(
,
i.e. , equal
to the temperature at the end of the cooling.
For instance, in the radiation field of NGC 2023 small PAHs
(
![]() )
eventually reach temperature as low as 15 K at time
)
eventually reach temperature as low as 15 K at time ![]() whereas bigger PAHs
(
whereas bigger PAHs
(
![]() )
remain at around 35 K.
)
remain at around 35 K.
In Fig. 4, we show
the cooling curves obtained for various energies per C-atom
![]() .
As expected, the
peak temperatures are identical for a given
.
As expected, the
peak temperatures are identical for a given ![]() .
We note that
the
.
We note that
the ![]() -curves do not change much for different
-curves do not change much for different ![]() -values while
-values while ![]() remains fixed: in fact if the emission cross-section were only proportional to
remains fixed: in fact if the emission cross-section were only proportional to ![]() all the cooling curves with (
all the cooling curves with (![]() ,
,
![]() )
combinations yielding the same
)
combinations yielding the same
![]() would merge. Cooling curves with larger
would merge. Cooling curves with larger ![]() have higher temperatures
because emission in the C-H modes is less important (in a fully
hydrogenated PAH we have
have higher temperatures
because emission in the C-H modes is less important (in a fully
hydrogenated PAH we have
![]() ). The small variation in the
). The small variation in the ![]() -curves at fixed
-curves at fixed ![]() then reflects the decrease of the emission cross-section per carbon atom with increasing size.
then reflects the decrease of the emission cross-section per carbon atom with increasing size.
As noted above, the observed similarity of the AIB profiles in our sample means that the range of PAH emission temperatures does not vary much: to test this idea, we determine here the temperature distribution of PAHs. Moreover, as we show below, the effect of the size distribution and exciting radiation field parameters are illustrated in a synthetic fashion in the temperature distribution.
The observed AIB spectrum results principally from the superposition of many blackbodies
at different temperatures (Eqs. (3) and (5)). Following Eq. (3) it is clear that
a given blackbody will have a significant contribution to the emergent
spectrum if its temperature T is high and/or if it remains a long time
at that temperature: a PAH with a temperature between T and
![]() (corresponding to the time interval
(corresponding to the time interval
![]() )
will thus contribute to the
total emitted luminosity
)
will thus contribute to the
total emitted luminosity ![]() (see the end of Sect. 4.1) with a weight proportional to
(see the end of Sect. 4.1) with a weight proportional to
![]() or the fraction of the total available energy,
or the fraction of the total available energy, ![]() (the energy of the absorbed photon), that is dissipated
between t and
(the energy of the absorbed photon), that is dissipated
between t and
![]() .
This definition of the temperature weight is different from previous work
(Draine & Anderson 1985; Désert et al. 1986) which only considered the time that
a given grain spends in the temperature interval
.
This definition of the temperature weight is different from previous work
(Draine & Anderson 1985; Désert et al. 1986) which only considered the time that
a given grain spends in the temperature interval
![]() ,
namely dt/dT:
the present definition which takes into account the emitted power actually reflects
the contribution of a given temperature to the final spectrum.
,
namely dt/dT:
the present definition which takes into account the emitted power actually reflects
the contribution of a given temperature to the final spectrum.
From Eq. (7), we see that the temperature weight in the total luminosity is simply
![]() .
Taking into account the probability distribution of the exciting photons and the fraction
of PAHs containing
.
Taking into account the probability distribution of the exciting photons and the fraction
of PAHs containing ![]() carbon atoms, we define the temperature weight
carbon atoms, we define the temperature weight ![]() as:
as:
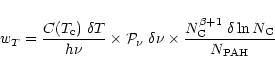 |
(10) |
To obtain the PAH temperature distribution in a given exciting radiation field, we build the
histogram of all cooling curves for all molecular sizes in temperature bins of constant size
(
![]() K), each temperature T being given the weight wT.
K), each temperature T being given the weight wT.
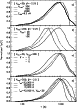 |
Figure 5:
The distribution of PAH temperatures
|
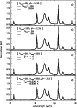 |
Figure 6:
The spectral energy densities corresponding to the temperature distributions shown in Fig. 5.
All the curves have been normalized to 1 at the peak value of the 7.7 |
From our weight definition, p(T)dT is the fractional contribution of all PAHs with temperatures
in the range
![]() to the total emitted luminosity
to the total emitted luminosity ![]() .
.
The PAH temperature distributions, normalized to 1 at their peak values to facilitate the comparison, are shown in Fig. 5:
they all present a maximum between 300 and 800 K.
The shape of these distributions can be understood as follows. Assuming that all molecules absorb a photon of energy
![]() ,
the temperature weights are proportional to
,
the temperature weights are proportional to
![]() .
At low T, all the C(T)-curves corresponding
to the different
.
At low T, all the C(T)-curves corresponding
to the different ![]() 's sum up to give wT. As the temperature increases, the largest molecules do not contribute anymore to wT
because they are too cold: this fade out more than compensates for the rise of C(T) with the temperature and produces a maximum in the
temperature distribution.
's sum up to give wT. As the temperature increases, the largest molecules do not contribute anymore to wT
because they are too cold: this fade out more than compensates for the rise of C(T) with the temperature and produces a maximum in the
temperature distribution.
Figure 5 illustrates the sensitivity of the PAH temperature distribution to the size distribution parameters,
![]() ,
,
![]() and
and ![]() (Figs. 5a to 5c) and to the hardness of the exciting radiation
field, parameterized as
(Figs. 5a to 5c) and to the hardness of the exciting radiation
field, parameterized as
![]() (Fig. 5d). The associated changes in the AIB spectrum are shown in Fig. 6.
In all these figures (except the M17-SW case in Fig. 5d), we used the same dilution factor for the radiation field
(
(Fig. 5d). The associated changes in the AIB spectrum are shown in Fig. 6.
In all these figures (except the M17-SW case in Fig. 5d), we used the same dilution factor for the radiation field
(
![]() ,
corresponding to NGC 2023): indeed, as long as one is in the regime of temperature fluctuations,
the spectral distribution of the PAH emission spectrum does not depend on the radiation field intensity (Sellgren 1984) while its
absolute level scales with it (see Eq. (3)). Moreover, for the purpose of comparison, all the spectra of Fig. 6 have been normalized
to 1 at the peak value of the 7.7
,
corresponding to NGC 2023): indeed, as long as one is in the regime of temperature fluctuations,
the spectral distribution of the PAH emission spectrum does not depend on the radiation field intensity (Sellgren 1984) while its
absolute level scales with it (see Eq. (3)). Moreover, for the purpose of comparison, all the spectra of Fig. 6 have been normalized
to 1 at the peak value of the 7.7 ![]() m-band because its profile is independent of the PAH temperature (see Sect. 4.1).
m-band because its profile is independent of the PAH temperature (see Sect. 4.1).
In Fig. 5a, we consider the effect of taking the full spectral distribution of exciting photons
instead of the same mean absorbed photon energy,
![]() (i.e. ,
(i.e. ,
![]() ).
In the following, we will refer to the
).
In the following, we will refer to the
![]() -approximation whenever it is assumed that each molecule absorbs the
same photon of energy
-approximation whenever it is assumed that each molecule absorbs the
same photon of energy
![]() at the rate
at the rate
![]() in the given radiation field. The
in the given radiation field. The
![]() -approximation
only affects the high temperature tail of the distribution. As we will see in Sect. 4.4.2, this tail matters for
the width of the 3.3
-approximation
only affects the high temperature tail of the distribution. As we will see in Sect. 4.4.2, this tail matters for
the width of the 3.3 ![]() m-band. Nevertheless, the rest of the AIB spectrum is little affected by the
m-band. Nevertheless, the rest of the AIB spectrum is little affected by the
![]() -approximation.
-approximation.
![]() has a weak influence on the temperature distribution (Fig. 5b) and its impact, which is most noticeable at long
wavelengths (
has a weak influence on the temperature distribution (Fig. 5b) and its impact, which is most noticeable at long
wavelengths (
![]() 10
10 ![]() m, see Fig. 6a), is easily drowned by small changes of
m, see Fig. 6a), is easily drowned by small changes of ![]() ,
the index of the
power-law size distribution of PAHs (see Figs. 5c and 6c). When
,
the index of the
power-law size distribution of PAHs (see Figs. 5c and 6c). When ![]() decreases, the contribution of the smallest PAHs
becomes more important and the cold tail of the temperature distribution is somewhat reduced (Fig. 5c): this leads to an enhanced
3.3/11.3
decreases, the contribution of the smallest PAHs
becomes more important and the cold tail of the temperature distribution is somewhat reduced (Fig. 5c): this leads to an enhanced
3.3/11.3 ![]() m-band ratio and to somewhat broader bandwidths (Fig. 6c and Figs. 8 to 11).
Note that, due to this broadening, the band peak value diminishes
(see the 6.2
m-band ratio and to somewhat broader bandwidths (Fig. 6c and Figs. 8 to 11).
Note that, due to this broadening, the band peak value diminishes
(see the 6.2 ![]() m-band in Fig. 6c) because the band integrated cross-section is conserved with temperature.
Both
m-band in Fig. 6c) because the band integrated cross-section is conserved with temperature.
Both ![]() and
and
![]() (which determines
(which determines
![]() ,
here
,
here
![]() to 45000 K corresponds to
to 45000 K corresponds to
![]() to 9 eV)
affect the hot tail of p(T) (Figs. 5b and 5d) which merely reflects the hottest part of the cooling curve
(Fig. 4).
This behaviour of p(T) follows from the fact that the PAH peak temperature only depends on the energy content per carbon atom in a molecule,
to 9 eV)
affect the hot tail of p(T) (Figs. 5b and 5d) which merely reflects the hottest part of the cooling curve
(Fig. 4).
This behaviour of p(T) follows from the fact that the PAH peak temperature only depends on the energy content per carbon atom in a molecule,
![]() (see Sect. 4.2) and that a typical value for
(see Sect. 4.2) and that a typical value for ![]() is
is
![]() (
(![]() is close to the mean value of
is close to the mean value of ![]() because of the
steep power-law size distribution). In fact, the temperature distribution and the shape of the emission spectrum are similar for different
because of the
steep power-law size distribution). In fact, the temperature distribution and the shape of the emission spectrum are similar for different
![]() -couples yielding the same energy per carbon atom. As expected, an increase of
-couples yielding the same energy per carbon atom. As expected, an increase of ![]() leads to colder PAHs (Fig. 5b)
which contribute more to the long-wavelength bands (Fig. 6b) while an increase of
leads to colder PAHs (Fig. 5b)
which contribute more to the long-wavelength bands (Fig. 6b) while an increase of
![]() has the reverse effect (see Figs. 5d and 6d).
We pointed out earlier that the PAH temperature distribution must remain unchanged in order to explain the similarity of the observed AIB profiles:
we show in Fig. 5d that this condition is fulfilled if
has the reverse effect (see Figs. 5d and 6d).
We pointed out earlier that the PAH temperature distribution must remain unchanged in order to explain the similarity of the observed AIB profiles:
we show in Fig. 5d that this condition is fulfilled if ![]() is raised along with
is raised along with
![]() .
Specifically, an increase of
.
Specifically, an increase of
![]() from
23000 K (the case of NGC 2023) to 45000 K (the case of M17-SW) requires
from
23000 K (the case of NGC 2023) to 45000 K (the case of M17-SW) requires
![]() to 30, respectively.
In the next sections, we show that this requirement allows to consistently reproduce the overall AIB spectrum as well as the individual band
profiles.
to 30, respectively.
In the next sections, we show that this requirement allows to consistently reproduce the overall AIB spectrum as well as the individual band
profiles.
We now present the PAH IR-emission as computed from the formalism described above in the case of NGC 2023 and M17-SW. We selected these two objects because they present the largest contrast in the effective temperature of the exciting radiation field: we therefore expect these spectra to provide the strongest constraints on our model.
Having determined the temperature distribution of a population of PAHs, we can
now compute the corresponding IR emission using Eqs. (3) and (5).
The PAH size distribution parameters were constrained as follows.
We note that the overall shape of the 3-13 ![]() m AIB spectrum which is dominated by emission from molecules at
m AIB spectrum which is dominated by emission from molecules at
![]() K is not much affected by changes in
K is not much affected by changes in ![]() or
or ![]() (see Figs. 6a and 6c).
For simplicity, we fix from now on
(see Figs. 6a and 6c).
For simplicity, we fix from now on
![]() .
First,
.
First, ![]() is fixed so as to reproduce
the observed 3.3/11.3
is fixed so as to reproduce
the observed 3.3/11.3 ![]() m-band ratio in a given exciting radiation field (described by
m-band ratio in a given exciting radiation field (described by
![]() ):
we require
):
we require
![]() in NGC 2023 while
in NGC 2023 while
![]() in M17-SW. The hydrogenation fraction,
in M17-SW. The hydrogenation fraction, ![]() ,
is
constrained from the 7.7/11.3
,
is
constrained from the 7.7/11.3 ![]() m-band ratio: a good match to the observed band ratios is obtained with
m-band ratio: a good match to the observed band ratios is obtained with
![]() for NGC 2023 and
for NGC 2023 and
![]() for M17-SW.
The index of the power law size distribution,
for M17-SW.
The index of the power law size distribution, ![]() ,
can be constrained from the requirement that the
predicted 16.4
,
can be constrained from the requirement that the
predicted 16.4 ![]() m-band (on top of the broadband continuum) matches the observed band:
we find that
m-band (on top of the broadband continuum) matches the observed band:
we find that
![]() reproduces the 16.4
reproduces the 16.4 ![]() m-band well in both objects
m-band well in both objects![]() .
Unfortunately, individual PAH species show a large spread in the integrated
cross-section of the 16.4
.
Unfortunately, individual PAH species show a large spread in the integrated
cross-section of the 16.4 ![]() m-band (see Table 3 of Moutou et al. 1996) which does not constrain
m-band (see Table 3 of Moutou et al. 1996) which does not constrain ![]() :
specifically, to match the observed 16.4
:
specifically, to match the observed 16.4 ![]() m-band we require
m-band we require
![]() for the lowest
cross-section value while
for the lowest
cross-section value while
![]() for the largest cross-section value.
More laboratory work on PAHs is warranted in order to understand the trend of the 16.4
for the largest cross-section value.
More laboratory work on PAHs is warranted in order to understand the trend of the 16.4 ![]() m-band
profile with respect to
m-band
profile with respect to ![]() and to the various isomer states.
As discussed by PJB, an additional constraint on
and to the various isomer states.
As discussed by PJB, an additional constraint on ![]() is provided by the intensity and width of the AIB
profiles (see the next section).
The
is provided by the intensity and width of the AIB
profiles (see the next section).
The ![]() -value can then be adjusted in order to
match the peak position and the FWHM of the 3.3
-value can then be adjusted in order to
match the peak position and the FWHM of the 3.3 ![]() m-band (see Sect. 4.4.2): in fact, the value of -3.5 found
from the 16.4
m-band (see Sect. 4.4.2): in fact, the value of -3.5 found
from the 16.4 ![]() m-band gives a good fit in the case of NGC 2023 and M17-SW (see Fig. 8).
m-band gives a good fit in the case of NGC 2023 and M17-SW (see Fig. 8).
At this point, it is interesting to note that that the 6-to-13 ![]() m part of the spectrum is produced by
molecules with emission temperatures between 400 and 1000 K. During temperature fluctuations,
most PAHs go through these temperatures:
this is why the maximum of the temperature distribution (Fig. 5) always falls in this range.
In fact, the emission of any PAH with
m part of the spectrum is produced by
molecules with emission temperatures between 400 and 1000 K. During temperature fluctuations,
most PAHs go through these temperatures:
this is why the maximum of the temperature distribution (Fig. 5) always falls in this range.
In fact, the emission of any PAH with
![]() shows ratios of band
peak values which are quite comparable to the observed 6-13
shows ratios of band
peak values which are quite comparable to the observed 6-13 ![]() m AIB spectrum (see PJB and Draine & Li 2001).
On the other hand,
the match of the observed band position and width in the present data sample and in CAM-CVF spectra of similar
interstellar regions requires small molecules (see next section). However, taking into account the
full size distribution of PAHs will add emission mostly at 3.3
m AIB spectrum (see PJB and Draine & Li 2001).
On the other hand,
the match of the observed band position and width in the present data sample and in CAM-CVF spectra of similar
interstellar regions requires small molecules (see next section). However, taking into account the
full size distribution of PAHs will add emission mostly at 3.3 ![]() m (from the smaller species, see Fig. 6b) and in the far-infrared
(from the larger species, see Fig. 6a) without changing much the 6-13
m (from the smaller species, see Fig. 6b) and in the far-infrared
(from the larger species, see Fig. 6a) without changing much the 6-13 ![]() m region. Thus, in the framework of the present
model, the observed invariance of the AIB spectrum in CAM-CVF data (6-16
m region. Thus, in the framework of the present
model, the observed invariance of the AIB spectrum in CAM-CVF data (6-16 ![]() m) implies that the AIB
carriers are small enough to undergo large temperature fluctuations (at least 400 K) during which
they emit in this wavelength range.
m) implies that the AIB
carriers are small enough to undergo large temperature fluctuations (at least 400 K) during which
they emit in this wavelength range.
Our best fit SED's are displayed in Fig. 7: we assumed a total column density of
![]() cm-2 (i.e. , 1 visible magnitude of extinction) for both NGC 2023 and M17-SW with
10% and 8%, respectively of the interstellar carbon in PAH cations (using [C/H]
cm-2 (i.e. , 1 visible magnitude of extinction) for both NGC 2023 and M17-SW with
10% and 8%, respectively of the interstellar carbon in PAH cations (using [C/H]
![]() ,
Snow & Witt 1996). The hydrogenation fraction of PAHs was taken to be 80% for NGC 2023 and 50% for M17-SW.
To compare in a meaningful fashion the predicted PAH emission to the observed spectrum, the broadband continuum described
in Sect. 3 has been added to our model spectrum. This continuum consists of the modified blackbody along with
the 1000 and 1450 cm_1 broad profiles (in M17-SW an additional broad profile at 600 cm_1 is required,
see Fig. 2). All the main AIBs (at 3.3, 6.2, 7.7, 8.6 and 11.3
,
Snow & Witt 1996). The hydrogenation fraction of PAHs was taken to be 80% for NGC 2023 and 50% for M17-SW.
To compare in a meaningful fashion the predicted PAH emission to the observed spectrum, the broadband continuum described
in Sect. 3 has been added to our model spectrum. This continuum consists of the modified blackbody along with
the 1000 and 1450 cm_1 broad profiles (in M17-SW an additional broad profile at 600 cm_1 is required,
see Fig. 2). All the main AIBs (at 3.3, 6.2, 7.7, 8.6 and 11.3 ![]() m) are matched within 20%.
We note that the model fails to reproduce the 12.7
m) are matched within 20%.
We note that the model fails to reproduce the 12.7 ![]() m-band in M17-SW: this may be due to an ill-definition of the
underlying broadband continuum in this complex spectral region (see Fig. 2).
The AIB spectrum corresponding to the neutral
PAHs (we took the IR cross-sections from Léger et al. 1989b) is shown in the case of NGC 2023 with a PAH
abundance corresponding to 6% of the interstellar carbon, with
m-band in M17-SW: this may be due to an ill-definition of the
underlying broadband continuum in this complex spectral region (see Fig. 2).
The AIB spectrum corresponding to the neutral
PAHs (we took the IR cross-sections from Léger et al. 1989b) is shown in the case of NGC 2023 with a PAH
abundance corresponding to 6% of the interstellar carbon, with
![]() ,
,
![]() and
and
![]() .
The
.
The ![]() -value was fixed so as to reproduce the position and width of the 3.3
-value was fixed so as to reproduce the position and width of the 3.3 ![]() m-band (see next section)
and it is the same as for the cations.
In the case of neutral PAHs, the C-C/C-H band ratio is reduced by about one order
of magnitude with respect to the cations. Matching the observed AIB with neutral PAHs would require a very low
hydrogen coverage (
m-band (see next section)
and it is the same as for the cations.
In the case of neutral PAHs, the C-C/C-H band ratio is reduced by about one order
of magnitude with respect to the cations. Matching the observed AIB with neutral PAHs would require a very low
hydrogen coverage (
![]() )
which would produce a strongly discrepant 8.6
)
which would produce a strongly discrepant 8.6 ![]() m-band and also would be at
odds with theoretical predictions on the hydrogen coverage of PAHs (Allain et al. 1996).
m-band and also would be at
odds with theoretical predictions on the hydrogen coverage of PAHs (Allain et al. 1996).
In the following,
we compare in detail the profiles of the observed 3.3, 6.2, 8.6 and
11.3![]() m-AIBs to our model results: we restrict our comparison to these bands
because they are well defined in the data and involve a small number of Lorentz fit
components.
m-AIBs to our model results: we restrict our comparison to these bands
because they are well defined in the data and involve a small number of Lorentz fit
components.
In order to highlight the match in band width and position,
our model profiles are compared to the observed AIBs in a normalized fashion.
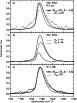 |
Figure 9:
Same as Fig. 8 for the 6.2 |
Figures 8 to 11 show our model representation of the AIB profiles. The contribution of vibrational
hot bands are not included in our model profiles: in the case of the 6.2 and 11.3 ![]() m-bands, hot
bands provide an additional broadening of less than 5 cm_1 (PJB).
In Fig. 8c, we note the effect of making the
m-bands, hot
bands provide an additional broadening of less than 5 cm_1 (PJB).
In Fig. 8c, we note the effect of making the
![]() -approximation
(i.e., all molecules are heated
by photons of the
same energy
-approximation
(i.e., all molecules are heated
by photons of the
same energy
![]() ,
see Sect. 4.3): the lack of the hot tail in the PAH temperature distribution yields a
narrower band profile. Hence, using this approximation would lead to an underestimate of
,
see Sect. 4.3): the lack of the hot tail in the PAH temperature distribution yields a
narrower band profile. Hence, using this approximation would lead to an underestimate of
![]() :
e.g., in the case of NGC 2023,
:
e.g., in the case of NGC 2023,
![]() is required to match the observed 3.3
is required to match the observed 3.3 ![]() m-band if one
makes the
m-band if one
makes the
![]() -approximation.
This approximation has, however, negligible consequences for the other bands.
The effect of a larger
-approximation.
This approximation has, however, negligible consequences for the other bands.
The effect of a larger ![]() ,
-2.25 (corresponding to the classical power-law exponent of -3.5 when the size
distribution is expressed in terms of the grain radius,
Mathis et al. 1977) is shown as the dashed line in Figs. 8a to 11a: a low
,
-2.25 (corresponding to the classical power-law exponent of -3.5 when the size
distribution is expressed in terms of the grain radius,
Mathis et al. 1977) is shown as the dashed line in Figs. 8a to 11a: a low ![]() -value is
clearly required to match the observed band profiles. Decreasing
-value is
clearly required to match the observed band profiles. Decreasing ![]() ,
however, has a moderate impact
on the band profiles because the then enhanced contribution of small molecules
is compensated by a strong increase of the band width leading to a decrease in intensity
(the integrated cross-sections of the IR bands,
,
however, has a moderate impact
on the band profiles because the then enhanced contribution of small molecules
is compensated by a strong increase of the band width leading to a decrease in intensity
(the integrated cross-sections of the IR bands,
![]() ,
are assumed to be conserved
with temperature).
,
are assumed to be conserved
with temperature).
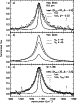 |
Figure 10:
Model results for the 8.6 |
The harder radiation field of M17-SW results in PAHs at higher temperatures
(see Fig. 5d), consequently the model AIB-profiles are clearly too broad and redshifted
(see the dashed line in the bottom panel of Figs. 8 to 11) if we use the same size distribution
as for NGC 2023. For the profile width and position,
![]() is also required in
order to match the observed AIBs of M17-SW. This change of
is also required in
order to match the observed AIBs of M17-SW. This change of ![]() has a physical
interpretation: the photo-dissociation and fragmentation rates rise steeply
with the molecular temperature (Léger et al. 1989a). The
has a physical
interpretation: the photo-dissociation and fragmentation rates rise steeply
with the molecular temperature (Léger et al. 1989a). The ![]() values we find are smaller than the theoretical predictions of Allain et al. (1996).
values we find are smaller than the theoretical predictions of Allain et al. (1996).
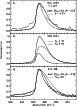 |
Figure 11:
Same as Fig. 9 for the 11.3 |
Except for the 8.6 ![]() m-band, all AIB profiles are well explained by the PAH emission model.
The hot (small) molecules dominate the emission profiles, in particular in the AIB wings;
they also produce the observed red asymmetry (6.2 and 11.3
m-band, all AIB profiles are well explained by the PAH emission model.
The hot (small) molecules dominate the emission profiles, in particular in the AIB wings;
they also produce the observed red asymmetry (6.2 and 11.3![]() m-bands). The cool (large) molecules
contribute the blue wing of the AIB. We want to stress that this match of the AIBs is obtained
by using the cross-sections and profile temperature dependence measured on small molecules: no
additional broadening, reflecting the decrease of the level lifetime with increasing
molecular size (see Sect. 5), has been taken into account here.
m-bands). The cool (large) molecules
contribute the blue wing of the AIB. We want to stress that this match of the AIBs is obtained
by using the cross-sections and profile temperature dependence measured on small molecules: no
additional broadening, reflecting the decrease of the level lifetime with increasing
molecular size (see Sect. 5), has been taken into account here.
The observed width of the 8.6 ![]() m-band is not at all reproduced by the temperature broadening
law derived from laboratory work. In fact, a broadening 5.5 times faster (
m-band is not at all reproduced by the temperature broadening
law derived from laboratory work. In fact, a broadening 5.5 times faster (
![]() cm_1/K) with temperature would match the observations (see Fig. 10). In this latter case,
we note that (i) the symmetrical shape of the 8.6
cm_1/K) with temperature would match the observations (see Fig. 10). In this latter case,
we note that (i) the symmetrical shape of the 8.6 ![]() m-band is well explained by the slow
redshift of the band centroid with temperature (
m-band is well explained by the slow
redshift of the band centroid with temperature (
![]() cm_1/K whereas the other
AIBs have 2 to
cm_1/K whereas the other
AIBs have 2 to
![]() cm_1/K) and (ii) the emission of large molecules dominates the
core of the 8.6
cm_1/K) and (ii) the emission of large molecules dominates the
core of the 8.6 ![]() m-band (conversely to the other AIBs).
m-band (conversely to the other AIBs).
We have not modelled the 7.7 ![]() m-band because it includes several components whose assignment
to features in laboratory spectra of PAHs is not straightforward. However, it is interesting
to note that the observed width (23 to 29 cm_1) of the 7.6
m-band because it includes several components whose assignment
to features in laboratory spectra of PAHs is not straightforward. However, it is interesting
to note that the observed width (23 to 29 cm_1) of the 7.6 ![]() m-band (see Sect. 3) is comparable
to the width predicted by PJB.
m-band (see Sect. 3) is comparable
to the width predicted by PJB.
We emphasize here that the model profile of a PAH emission band is the result of the superposition
of many Lorentz profiles conversely to the implicit assumption behind the decomposition performed in Sect. 3.
Consider for instance a PAH containing ![]() carbon atoms which has been heated
by a photon of energy
carbon atoms which has been heated
by a photon of energy ![]() :
the emerging band profile of this molecule will be the sum
of all the Lorentz profiles corresponding to the temperatures of the cooling curve,
:
the emerging band profile of this molecule will be the sum
of all the Lorentz profiles corresponding to the temperatures of the cooling curve,
![]() (i.e. , the time integral in Eq. (3)). The total band profile of a PAH interstellar population is eventually
obtained from the weighted sum of the emerging band profiles from all molecules, for all energies of the
exciting photon (see Eqs. (3) and (5)).
(i.e. , the time integral in Eq. (3)). The total band profile of a PAH interstellar population is eventually
obtained from the weighted sum of the emerging band profiles from all molecules, for all energies of the
exciting photon (see Eqs. (3) and (5)).
Copyright ESO 2001