5 Photometry, noise analysis, accuracy

   
5.1 Flux measurements by aperture photometry

Once a detection is obtained on source maps, fluxes have to be measured in final maps. Simulations of point sources on a flat background permit derivation of the effective average footprint on the map, which results from the PHT footprint and the final pixeling obtained in a given field, which depends on the exact timing of the observations (roll angle).

We check that strong sources in the data have a profile in agreement with the effective footprint. The growth curve of the effective footprint is plotted in Fig. 4. The determination of the parameters for the aperture photometry filter is performed by measurements of the flux of simulated sources through different sets of apertures. We find that the following values minimize the noise: an internal radius of 90 arcsec for measuring the source and an external radius of 120 arcsec to estimate the background. The determination of the flux takes into account the fact that at these radii we select only a part of the effective footprint, and includes the appropriate correction.

Figure 4: Growth curve of the effective footprint on a logarithmic scale with the location of the radii of circles used for aperture photometry; dotted vertical line: 90 arcsecond for the inner radius; dashed vertical line: 120 arcsecond for the outer radius.

In order not to be biased by a nearby strong source which could affect the estimate of the local background in a measurement, we used a CLEAN-like procedure. We first compute a temporary catalog that we sort by decreasing flux. Then we measure the brightest source, and remove it, and repeat this process through the whole catalog. Note that this procedure is not used to extract faint sources but only to improve the photometry of sources detected before applying the CLEAN procedure.

At the end of the process, we add 10% to the source flux to account for the transient behaviour of the detector. This value is derived from our absolute measurement in the FSM1 (using AOT P25) in which the instantaneous response and the following transient, as well as the final flux after 256 s, are observed (Lagache & Dole 2001).

5.2 Confusion noise

We made 10000 measurements on each field at random positions, and obtained distributions which are shown in Figs. 5, 6 and 7. These distributions represent the probability of measurements by aperture photometry on a field with sources and dominated by confusion. They are fitted in their central part by a Gaussian, whose dispersion is an estimate of the confusion noise. The distributions are plotted in Figs. 5 to 7. The assymetric part at high flux levels reflects the counts of bright sources. We finally derive $\sigma_{\rm c} \simeq 45$ mJy for the confusion noise in all of the FIRBACKfields (41 mJy for FSM, 44 for FN1 and 46 mJy for FN2). The $3 \sigma_{\rm c}$ level is thus 135 mJy and $4 \sigma_{\rm c}~ 180$ mJy.

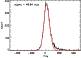Figure 5: 10000 random aperture photometry measurements on the FSM map indicating the confusion noise. The small excess at high flux levels is due to real sources in the data.

Figure 6: 10000 random aperture photometry measurements on FN1.

Figure 7: 10000 random aperture photometry measurements on FN2.

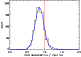Figure 8: Histogram of the ratio of measured flux to input flux, when sources of 500 mJy are added to the maps.

This estimate is compatible with the classical definition of the confusion, by computing the number of independent beams in all the FIRBACK fields: with a FWHM of 94 arcsec at 170 $\mu$m in a 3.89 sq. deg surface, we have about 5700 independent beams. At the $3 \sigma$ limit, that is above 135 mJy, we have 196 sources (see Sect. 6), there are about 29 beams per source - in good agreement with the classical definition of the confusion of 30 independent beams per source for sources brighter that $3 \sigma_{\rm c}$. If we have a catalogue cutoff at $4 \sigma _{\rm c}$ (resp. $5 \sigma_{\rm c}$), we obtain 54 (resp 91) independents beams per source. Our analysis is compatible with the simulations of Hogg (2000), who shows that 30 beams per source is a minimum where source counts are steep, and suggests a threshold at about 50 beams per source.

The cirrus fluctuations have a low probability of creating spurious sources at this level of HI column-density, as shown in previous works, such as Gautier et al. (1992), Lagache (1998), Kawara et al. (1998), Puget et al. (1999), and Juvela et al. (2000).

5.3 Detector noise

The first field to be observed in our investigations was FSM1, and the goal was to demonstrate the ability of doing a deep far infrared survey limited by confusion rather than detector noise. With four independent rasters mapping exactly the same sky, that is 16 independent measurements, Lagache (1998) and Puget et al. (1999) show that the detector noise level is about 3 mJy $1 \sigma$, i.e. far below the confusion noise and thus neglected.

Figure 9: Detected sources on FN1 field. Circles are sources from the ISO FIRBACK Source Catalog ( $S_{\nu } > 180$ mJy) and squares are sources from the Complementary ISO FIRBACK Source Catalog ( $135 < S_{\nu } < 180$ mJy).

5.4 Photometric accuracy

The histograms of the ratio of recovered flux to input flux of the simulated sources are used to estimate the offset and the error of the fluxes. One of these histograms is shown in Fig. 8 for the FN1 field and 500 mJy sources.

One can see a systematic offset of the distribution's peak with respect to the input flux. This offset is constant for a given field, and equals 16%, 19%, 18% and 16% for the FN1, FN2, FSM1 and FSM234 fields, respectively. The possible explanations for this offset are (1) the variation of the effective footprint inside the field (due to an inhomogeneous sampling of the sky) and (2) the loss of flux at the edges of the pixels. We apply this correction on the source fluxes.

The standard deviation of the fitted Gaussian, $\sigma _{\rm s}$, estimates the dispersion of the source flux measurements. Figure 10 shows the variation of $\sigma _{\rm s}$ in mJy as a function of the source flux in Jy, in the FN1 field; the variation is similar in the other fields. $\sigma _{\rm s}$ can be decomposed in two components:

$\bullet$

a constant component due to confusion noise $\sigma _{\rm c}$;

$\bullet$

a component ( $\sigma _{\rm p}$) proportional to the source flux, due to the difference between the mean effective footprint and the local effective footprint.

The data points are fitted by the quadratic sum of the constant and the proportional component $\sqrt {\sigma _{\rm c}^2 + \sigma _{\rm p}^2}$.

The source flux uncertainties are computed for each field; however, there is little field-to-field variation. The uncertainty in the source flux is about 25% near $3 \sigma_{\rm c}$ at low fluxes, about 20% near $5 \sigma_{\rm c}$ and decreases to about 10% at high flux levels (near 1 Jy).

5.5 Positional accuracy

The identification of the sources in the simulations allows us to derive the positional accuracy. We neglect the telescope absolute pointing error of 1 $^{\prime\prime}$ (Kessler 2000). Figure 11 shows the distribution of the distance offset between the input source and the extracted source positions. All sources brighter than 500 mJy - i.e. where the sample is complete (see Sect. 7.1) - are recovered inside a 65 $^{\prime\prime}$ radius: the mean recovered distance is 15 $^{\prime\prime}$, and 90% of the sample falls inside 28 $^{\prime\prime}$. Taking all the sources with flux levels brighter than 180 mJy, 90% of the sample is recovered inside a radius of 42 $^{\prime\prime}$. We conclude that 99% (respectively 93%) of the sources are found in a circle of radius of 50 $^{\prime\prime}$, and 98% (respectively 90%) in 42 $^{\prime\prime}$ when the sample is complete, above 500 mJy (respectively 180 mJy).

Figure 10: Evolution of $\sigma _{\rm s}$, standard deviation of measured flux on the histograms, as a function of the source flux (diamonds). $\sigma _{\rm s}$ can be decomposed in two components: (1) a constant component due to confusion noise $\sigma _{\rm c}$ (horizontal dashed line) and (2) a component proportional to the flux $\sigma _{\rm p}$(sloped dashed line). $\sigma _{\rm s}$ is fitted by $\sqrt {\sigma _{\rm c}^2 + \sigma _{\rm p}^2}$(solid line).

Figure 11: Histogram of distances of identifications in the simulations. All sources brighter than 500 mJy (where the sample is complete) in the three FIRBACK fields are shown. The solid line corresponds to the median at 13 arcsec and the dashed line at 15 arcsec.