3 Results

3.1 Vertical distribution

Figure 1 shows the vertical distribution of various molecules (dashed lines) and their singly deuterated counterparts (solid lines) at R=500 AU and at $t=9.5\; 10^5$ yr, which is a typical age of a T Tauri star. The disk is assumed to be less massive than the Kyoto model by an order of magnitude. The effects of X-rays from the central star are included. Throughout this paper, we will also present the results of models in which the mass is that of the Kyoto model, in which X-rays are turned off, and in which the time is changed. The low mass model is emphasized because in Paper I, we showed that it is consistent with the observational result of DM Tau by Dutrey et al. (1997).

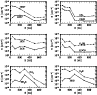Figure 2: The column densities of deuterated and normal species as a function of radius. The disk mass is assumed to be less than the Kyoto model by an order of magnitude. The disk age is $t=9.5\; 10^5$ yr

As can be seen in Fig. 1, most molecules have a peak abundance at some intermediate height; in the surface region of the disk the molecules are dissociated by UV photons both from the interstellar field and the central star, while close to the midplane most molecules are adsorbed onto grains. In the midplane region, however, some gas-phase species show a "late-time peak'' at $t\sim 10^5{-}10^6$ yr (Ruffle et al. 1997; Paper I) which can occur in gas-grain models with low sticking efficiencies or with non-thermal desorption. The high abundance of NH₃ in the midplane is caused by this peak.

A comparison of the concentrations of molecules and their deuterated isotopomers in Fig. 1 shows that molecular D/H ratios are much higher than the elemental abundance ratio D/H of $1.5\; 10^{-5}$. This is not surprising because deuterium fractionation proceeds in a similar way as in molecular clouds. Owing to the energy differences between deuterated species and normal species, and to some rapid exchange reactions, species such as H₃⁺ and CH₃⁺have a high D/H ratio, and the high ratio propagates to other species through ion-molecule reactions (Millar et al. 1989; Aikawa & Herbst 1999b). Another route to fractionation lies through the dissociative recombination of molecular ions with high D/H ratios, which leads to a high atomic D/H ratio. Neutral-neutral reactions involving H and D then propagate these high atomic D/H ratios. For example, a major production route for DCN is the reaction between D and H₂CN.

Figure 1 also shows that molecular D/H ratios are higher at smaller heights, where molecules are more heavily depleted from the gas phase onto grain surfaces. Molecular depletion enhances the D/H ratio of the remaining gaseous species. For example, H₂D⁺ is formed by the reaction H₃⁺ + HD and, in many situations, is destroyed mainly by the reaction H₂D⁺ + CO. Hence the ratio H₂D⁺/H₃⁺ is proportional to n(HD)/n(CO), which increases as the gaseous CO abundance decreases (Brown & Millar 1989). At sufficiently small CO densities, the dominant destruction route for H₂D⁺ becomes reaction with electrons or back reaction with H₂.

3.2 Radial distribution of D/H ratios

Figure 3: The column density ratios of deuterated to normal species as a function of radius. The disk mass is assumed to be less than the Kyoto model by an order of magnitude. The thick lines show the ratios at $t=9.5\; 10^5$yr, the thin lines at $t=3\; 10^5$ yr. The solid lines show models with X-rays and the dashed lines without X-rays

Figure 4: The column density ratios of deuterated to normal species as a function of radius, but for the Kyoto model. The thick lines show the ratios at $t=9.5\; 10^5$yr, the thin lines at $t=3\; 10^5$ yr. The solid lines show models with X-rays and the dashed lines without X-rays

By integrating the vertical distributions of molecular abundances, we obtain molecular column densities. The column densities of deuterated and normal species are shown in Fig. 2 for assorted molecules as a function of disk radius. The time is the same as in Fig. 1: $t=9.5\; 10^5$ yr. Despite the addition of direct and secondary ionization of heavy elements via X-rays in this paper, the calculated column densities of normal species are almost the same as in Paper I. One notable modification concerns the NH₃column density in the outermost region ( $R\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$>$ }}}500$ AU) of the disk. In Paper I, we assumed that the H₃⁺ + N reaction produces NH⁺; however, subsequent information shows that the reaction does not proceed efficiently (Scott et al. 1998). In the outer region, where N atoms are relatively abundant because of the low density, this reaction was a key component in the synthesis of NH₃. At R=700 AU in the lower mass model with X-rays and $t=9.5\; 10^5$ yr, the column density of NH₃ was $1.2\; 10^{12}$ cm^-2in Paper I, but it is only $6.7\; 10^{10}$ cm^-2 in the current model. At smaller radii ( $R\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}300$ AU) the modification is less significant.

We obtained averaged D/H ratios for molecules at each radius by dividing the column density of the deuterated species by that of the normal species. Figure 3 shows D/H ratios for the lower mass disk model, and Fig. 4 for the Kyoto model. The thick lines show the ratio at $t=9.5\; 10^5$ yr, and the thin lines at a shorter time of $3\; 10^5$ yr. The solid lines are for models with X-rays and the dashed lines for models without X-rays.

The radial dependence of the column density ratios shown in Figs. 3 and 4 can be understood from the major mechanism of deuteration. For example, the D/H ratios of NH₃, H₂O, and HCO⁺ decrease at $R\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}300$ AU. These three species are deuterated through H₂D⁺. Since the exothermicity for the reaction H₃⁺ + HD $\to$ H₂D⁺ + H₂is relatively low (230 K), the back reaction becomes important as the temperature rises near the star and lowers the D/H ratio in the inner regions. On the other hand, the D/H ratios in CH₄ and H₂CO do not decrease inwards, because those species are deuterated through CH₂D⁺, for which the exothermicity of the deuterium exchange reaction is much higher (370 K) than that for H₂D⁺. Finally, the DCN/HCN column density ratio slightly decreases inwards because D atoms are less abundant in inner regions.

X-rays affect the column density ratios. For $R\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$>$ }}}300$ AU, the D/H ratios of HCO⁺, NH₃ and H₂O are smaller in the case with X-rays than otherwise, because the enhancement of the H₂D⁺to H₃⁺ ratio is limited by the rate at which H₂D⁺ is destroyed by recombination with electrons, which are more abundant in the case with X-rays (Gu $\acute{\rm e}$lin et al. 1982; Caselli et al. 1998). In the inner regions, on the other hand, H₂D⁺ is always destroyed more efficiently by the reaction with CO or H₂, and thus the ratios are less dependent on the electron abundance.

The D/H ratios also depend on the total mass of the disk. Comparing Fig. 3 with Fig. 4, we can see that, except for DCO⁺/HCO⁺, the ratios are higher in the Kyoto model, especially in the outer region. This mass dependence is caused by molecular depletion onto grains, which is more efficient in disks with higher mass. This dependence does not appear for HCO⁺, because its abundance peaks at a larger height than those of neutral species, at which D/H ratios are less affected by depletion.

So far, detection of deuterated species has been reported only in the disk around LkCa15, where Qi (2000) observed DCN and HDO using the OVRO interferometer (see also Qi et al. 1999). He found DCN and HCN to be distributed within a radius of $\sim$1 $^{\prime\prime}$ (140 AU at the distance of 140 pc) and $\sim$3 $^{\prime\prime}$-4 $^{\prime\prime}$ from the central star, respectively. The differing sizes of the distributions reflect the fact that the only DCN line detected is the J=3-2transition. The column density of DCN was estimated to be $1\; 10^{13}$ cm^-2 from the integrated intensity of DCN(J=3-2), while the column density of HCN was estimated to be $\sim$10¹⁵ cm^-2 from the intensities of the H¹³CN J=3-2 and J=1-0 lines. Our model result for the DCN/HCN ratio within $R\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}200$ AU is consistent with the observation, independent of the disk mass. However, the absolute column densities of HCN and DCN in the model are significantly smaller than observed. In the region of radius $\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}200$ AU, the column density of DCN is $\sim$10¹¹ cm^-2 in our low mass disk model (Fig. 2) and is $\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}10^{12}$ cm^-2 in the Kyoto model (see Fig. 4 and Paper I). Moreover, the column densities of various molecules detected in LkCa15 are significantly higher than those in DM Tau (Qi 2000). One possible explanation for this difference would be the disk mass. The mass of the disk around LkCa15 is estimated to be 0.2 $M_{\odot}$ from the dust continuum, which traces the region of radius $\sim$100 AU, while the mass of Kyoto model within 100 AU is 0.024 $M_{\odot}$. In addition to modifying the Kyoto model to include higher masses, the major possibilities for improving our absolute column densities are (a) to lower the artificial sticking probability used in our current model (S=0.03) so that more material remains in the gas phase at a given time, or (b) to include specific non-thermal desorption mechanisms (Willacy & Langer 2000), and to consider the variability of their efficiency among disks. Finally, a K5 star HD284589, located close to LkCa15, may affect the molecular abundances in the disk through heating and/or UV radiation. These are prospects for future work. Observations of deuterated species in DM Tau would be desirable to compare with our current calculated values.

Like DCN, the estimated column density of HDO in LkCa15 - $(2{-}7)\; 10^{14}$ cm^-2 (Qi 2000) - is higher than the value ( $\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}1\; 10^{14}$ cm^-2) obtained in our models. Since H₂O cannot be observed from the ground, the HDO/H₂O ratio is not determined. It is interesting that the intensity peak of HDO is offset from the central star, which is consistent with our model.