The details of the Kyoto model are described in Paper I.
The column density of hydrogen nuclei
![]() (cm-2) and the temperature T(K) as functions
of R are given by the equations
(cm-2) and the temperature T(K) as functions
of R are given by the equations
The gas is in hydrostatic equilibrium in the vertical direction.
From the mass distribution given by Eq. (1) and
the temperature distribution given by Eq. (2), the density
distribution by number of hydrogen nuclei (cm-3) can be shown to be
We have extended
the network to include mono-deuterated analogues of hydrogen-bearing
species (Millar et al. 1989; Aikawa & Herbst 1999b). For normal
exothermic reactions and dissociative recombination reactions,
we have assumed that the total rate coefficient is unchanged
for deuterated analogues, and have also assumed statistical branching
ratios. There are some exceptions to the statistical rules; for
example,
the dissociative recombination of HCND+ does not produce
DCN but HCN. Similar rules are set for the hydrogenation of HCN and DCN,
i.e., HCN + H2DO+ produces HCND+ or HCNH+, but not DCNH+.
Another important exception is
We have included those deuterium exchange reactions for molecular ions and HD that are known to proceed in the laboratory or have been studied in detail theoretically (Millar et al. 1989); such reactions drive the fractionation yet are known to occur for only a few ions since activation energies are common (Henchman et al. 1988).
Although our model does not contain surface chemistry, as does the latest model of Willacy & Langer (2000), we do include the surface formation of H2 molecules, the surface recombination of ions and electrons, and formation and desorption of ice mantles. As in Paper I, we adopt an artificially low sticking probability S=0.03 for adsorbing species on the grain surface, in order to mimic the effect of non-thermal desorption. The sticking coefficient was originally chosen to fit the observed spectrum of CO emission lines in GG Tau. For thermal desorption from ice mantles, we adopt the same rate coefficients as in Aikawa et al. (1997). The total numbers of species and reactions included in our network are 773 and 10539, respectively.
The elemental abundances used here are the so-called "low-metal'' values
(e.g. Lee et al. 1998; Aikawa et al. 1999). The initial molecular
abundances are determined by following
molecular evolution in a precursor molecular cloud core with physical
conditions
![]() cm-3 and T=10 K up to
cm-3 and T=10 K up to
![]() yr, at which time observed abundances in molecular
clouds are reasonably reproduced (Terzieva & Herbst 1998).
yr, at which time observed abundances in molecular
clouds are reasonably reproduced (Terzieva & Herbst 1998).
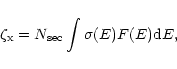 |
(5) |
Although the photoelectrons ionize mostly H2 and H,
the secondary ionization of heavy elements may be
important for their chemistry. Secondary ionization rate coefficients
for heavy elements are estimated by
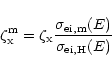 |
(7) |
The direct X-ray ionization rates for C, N, O, Si, S, Fe, Na, Mg, Cl and P are calculated at each point of the disk using the X-ray flux obtained from Eq. (6) and the ionization cross sections given by Verner et al. (1993). We assume primary ionization of heavy elements in a molecule leads to a doubly ionized species because of the Auger effect; the doubly ionized species then dissociate into two singly charged ions. We consider this destructive reaction only for simple diatomic molecules, because we do not know the products when polyatomic molecules are dissociated by X-rays. This simplification does not affect our results, because X-ray induced photolysis is much more efficient than direct ionization in terms of molecular destruction.
In fact, Eq. (8) assumes that induced photons are
absorbed by molecules locally; in other words, a spatial gradient of
![]() is not considered. Since
is not considered. Since
![]() is higher at
larger heights in our model, and
since induced photons can be emitted in the vertical direction of the disk,
the induced photons could penetrate deeper into the disk than we
estimate, especially in the outer radius (
is higher at
larger heights in our model, and
since induced photons can be emitted in the vertical direction of the disk,
the induced photons could penetrate deeper into the disk than we
estimate, especially in the outer radius (
![]() AU) in our lower
mass disk, in which the total column density is low (
AU) in our lower
mass disk, in which the total column density is low (
![]() mag). But a quantitative calculation of this effect requires a 2-D
radiation transfer calculation, which is beyond the scope of this paper.
mag). But a quantitative calculation of this effect requires a 2-D
radiation transfer calculation, which is beyond the scope of this paper.
A protoplanetary disk is irradiated by UV radiation from the external
interstellar field and from radiation due to the central star. The UV
flux from the central star varies temporally, and at R=100 AU the
unattenuated UV flux can reach a value 104 times higher than the
interstellar flux (Herbig & Goodrich 1986; Imhoff & Appenzeller
1987; Montmerle et al. 1993). As in Paper I, we utilize this maximum
value. The radiation fields from the two sources strike the disk from
different directions, and thus suffer different degrees of
attenuation. We obtain the attenuation of interstellar UV in terms of
the visual extinction ![]() ,
by calculating the vertical column
density from the disk surface to the height we are interested in,
using the relation
,
by calculating the vertical column
density from the disk surface to the height we are interested in,
using the relation
![]() cm-2mag-1]. The attenuation of the stellar UV,
cm-2mag-1]. The attenuation of the stellar UV,
![]() ,
is obtained by calculating the column density from the central star.
Values of
,
is obtained by calculating the column density from the central star.
Values of ![]() and
and
![]() are given in
Table 1 of Paper I, as a function of height at R=700 AU for the
Kyoto model. These values of extinction are then put into the
photo-rate equations of our network.
are given in
Table 1 of Paper I, as a function of height at R=700 AU for the
Kyoto model. These values of extinction are then put into the
photo-rate equations of our network.
In Sect. 4, where we report calculated values for molecular distributions in embedded disks, we consider an additional attenuation of 1-2 mag via ambient gas, while the attenuation of the stellar radiation is not modified.
Although the UV radiation is mainly attenuated by dust, self- and
mutual-shielding must be considered for H2 and CO (van Dishoeck & Black
1988; Lee et al. 1996), so that we must solve for
the molecular abundances and the UV attenuation self-consistently. As in
Paper I, we solve a one-dimensional slab model at each radius of the disk
and utilize modified shielding factors from Lee et al. (1996).
Copyright ESO 2001