| N | M1M2 | M1M3 | M2M3 |
| 3 | 0.80 | 0.19 | 0.01 |
| 4 | 0.81 | 0.15 | 0.03 |
| 5 | 0.81 | 0.15 | 0.04 |
| MC | 0.82 | 0.15 | 0.03 |
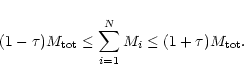 |
(1) |
| N | mass bin | BF(SD98) | BF+(SD98) | BF(MC) |
| 4 | 0.1-0.2 | 0.00 | 0.00 | 0.00 |
| 0.2-0.5 | 0.15 | 0.19 | 0.19 | |
| 0.5-1.2 | 0.52 | 0.68 | 0.64 | |
| >1.2 | 0.73 | 0.93 | 0.89 | |
| 5 | 0.1-0.2 | 0.01 | 0.01 | 0.00 |
| 0.2-0.5 | 0.15 | 0.25 | 0.21 | |
| 0.5-1.2 | 0.35 | 0.60 | 0.55 | |
| >1.2 | 0.56 | 0.91 | 0.86 |
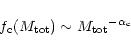 |
(2) |
![\begin{displaymath}f_{\rm s}(M) \sim
M^{-1}{\exp}\{-[\log_{10}(M/M_{\odot}) - \mu]^2/2\sigma^2\}
\end{displaymath}](/articles/aa/full/2001/21/aah2423/img30.gif) |
(3) |
Copyright ESO 2001