

Up: A two-step initial mass
Subsections
One of the fundamental goals of star formation theory is to
determine the relationship between molecular cloud conditions
and the mass and multiplicity distributions of the resulting
stars. To address aspects of this problem, Sterzik & Durisen
(1995, 1998, hereafter SD95 and SD98, respectively) used the
Mikkola & Aarseth (1990, 1993) chain regularizaton code to
compute the dynamic decay of nonhierarchical N-body clusters
with N = 3, 4, and 5.
It was already known from classic work
of the 1970's and earlier that, in the absence of dissipation,
the decay of pure point-mass few-body systems is dominated,
within a few tens of system crossing times, by the formation of
a hard binary which ejects most if not all the other stars
(e.g., van Albada 1968a,b; Standish 1972; Saslaw et al. 1974;
Harrington 1974, 1975; Heggie 1975;
Monaghan 1976a,b; Valtonen 1976).
In SD95 and SD98, the few-body
systems were explicitly interpreted as products of molecular
cloud core collapse and fragmentation. The decay products were
characterized statistically by considering large numbers of
cluster calculations for each choice of N with the goal of
determining distribution functions of fragment properties,
such as binary fractions and mass-ratio distributions.
For statistical studies of few-body systems, one must
adopt a procedure for choosing component stellar masses. One
common approach (e.g., McDonald & Clarke 1993, hereafter
McDC93) is to pick masses at random from an assumed stellar mass
spectrum (SMS). In this case, the SMS is also the overall
IMF for the stars. SD98 also introduced a two-step
process where they first chose a cluster total mass from a cluster
mass spectrum (CMS) and then required that the sum of the stellar
masses, chosen randomly from a different stellar mass spectrum (SMS),
should equal the chosen cluster mass. In this approach,
because random mass selections from the SMS which do not match the
chosen cluster mass are discarded, the final IMF of the selected
stars differs from the SMS through the imposition of the total cluster
mass constraint. In this paper, we refer to the distribution of
stellar masses which results from a large ensemble of such two-step
choices as a "two-step'' IMF. SD98 found
that the distributions of some binary properties agree better
with observations when stellar masses are chosen in this way.
The distribution which improves the most is
the overall binary fraction BF as a function of stellar mass M.
The reason for the improvement is straightforward.
Few-body cluster decay most often leads to production of one hard
binary from the two most massive stars, an effect referred
to as "dynamical biasing''. Assuming this always occurs, i.e.,
"complete'' dynamical biasing, McDC93 demonstrated that, when stars
are chosen at random from a realisitic IMF in a one-step process,
solar-mass stars almost always end up being in binaries for
small N. On the other hand, observations show that the BF
for nearby solar-type stars in the field is only
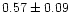 (Duquennoy & Mayor 1991, hereafter DM91). A
BF this low can be attained for
(Duquennoy & Mayor 1991, hereafter DM91). A
BF this low can be attained for 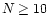 or so,
but then the mass ratio distribution does not agree well with
observations. Moreover, for
or so,
but then the mass ratio distribution does not agree well with
observations. Moreover, for 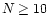 ,
the BF for
M stars becomes too low. Observations of field M stars
suggest BF in the range
,
the BF for
M stars becomes too low. Observations of field M stars
suggest BF in the range
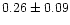 (Leinert et al. 1997,
hereafter L97) to
(Leinert et al. 1997,
hereafter L97) to
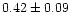 (Fischer & Marcy 1992,
hereafter FM92). With a two-step IMF, when total cluster masses are
chosen from a moderately steep and broad CMS,
solar-mass stars are often not the most massive stars
in their clusters. By the same token, for the same N,
M stars more often are the most
massive stars. The overall result is a more uniform distribution
of BF with mass from a single value of N.
(Fischer & Marcy 1992,
hereafter FM92). With a two-step IMF, when total cluster masses are
chosen from a moderately steep and broad CMS,
solar-mass stars are often not the most massive stars
in their clusters. By the same token, for the same N,
M stars more often are the most
massive stars. The overall result is a more uniform distribution
of BF with mass from a single value of N.
A two-step IMF might be a reasonable representation of
star cluster formation because the masses of stars in a small
cluster must be constrained to some extent by the total cloud
mass from which the cluster forms. For many years, Larson (1992) has
advocated that processes on different physical scales imprint
themselves on the IMF; and Elmegreen (1997) has also proposed
a related two-process IMF where the low and high-mass parts of the
IMF are shaped by different physical constraints. Observations by
Motte et al. (1998, hereafter Mot98) of  Ophiuchus
indicate that pre-collapse cloud cores can be already "fragmented''
into few-body systems of stellar mass clumps. These clumps do
appear to have the same mass spectrum as the IMF of young stars
in the same region (Luhman & Rieke 1999; Testi &
Sargent 1998). The observations seem consistent with the
"prompt fragmentation'' scenario (Clarke & Pringle 1991, 1993)
which is the starting point of the McDC93 analyses.
Of course, there are other ways to explain the observed BF(M).
For instance, McDonald & Clarke (1995, hereafter McDC95)
showed that cluster evolutions which include the dissipative
effects of collisions involving massive circumstellar disks give a
flatter BF(M). Cluster evolution will also deviate from
point-mass dynamics when cluster fragments accrete
competitively in a gas-rich environment (e.g.,
Zinnecker 1982; Burkert & Bodenheimer 1996; Bonnell et al. 1997;
1998, Smith et al. 1997; Bate 1999).
One could also appeal to slow dissolution of clusters through
loss of residual gas. All these effects would drive results
away from pure dynamical biasing.
In light of the many uncertainties,
we do not claim that a two-step IMF is the final or only answer.
Our objective here is to illustrate, by using reasonable
choices of the CMS and SMS and by making some simple
statistical calculations based on the results of SD98,
that a two-step IMF does improve binary characteristics and
therefore needs to be kept in mind as a possibly important
component of the star formation process, at least in a statistical
sense. We do not attempt to explain the stellar IMF itself but
choose our parameters so that the IMF resulting from our
Monte Carlo approach is reasonable.
Section 2 describes our methodology and offers some
motivation for our choices of mass spectra and other parameters.
Our main results are given in Sect. 3 and discussed briefly
in Sect. 4. Section 5 summarizes our conclusions.
Ophiuchus
indicate that pre-collapse cloud cores can be already "fragmented''
into few-body systems of stellar mass clumps. These clumps do
appear to have the same mass spectrum as the IMF of young stars
in the same region (Luhman & Rieke 1999; Testi &
Sargent 1998). The observations seem consistent with the
"prompt fragmentation'' scenario (Clarke & Pringle 1991, 1993)
which is the starting point of the McDC93 analyses.
Of course, there are other ways to explain the observed BF(M).
For instance, McDonald & Clarke (1995, hereafter McDC95)
showed that cluster evolutions which include the dissipative
effects of collisions involving massive circumstellar disks give a
flatter BF(M). Cluster evolution will also deviate from
point-mass dynamics when cluster fragments accrete
competitively in a gas-rich environment (e.g.,
Zinnecker 1982; Burkert & Bodenheimer 1996; Bonnell et al. 1997;
1998, Smith et al. 1997; Bate 1999).
One could also appeal to slow dissolution of clusters through
loss of residual gas. All these effects would drive results
away from pure dynamical biasing.
In light of the many uncertainties,
we do not claim that a two-step IMF is the final or only answer.
Our objective here is to illustrate, by using reasonable
choices of the CMS and SMS and by making some simple
statistical calculations based on the results of SD98,
that a two-step IMF does improve binary characteristics and
therefore needs to be kept in mind as a possibly important
component of the star formation process, at least in a statistical
sense. We do not attempt to explain the stellar IMF itself but
choose our parameters so that the IMF resulting from our
Monte Carlo approach is reasonable.
Section 2 describes our methodology and offers some
motivation for our choices of mass spectra and other parameters.
Our main results are given in Sect. 3 and discussed briefly
in Sect. 4. Section 5 summarizes our conclusions.


Up: A two-step initial mass
Copyright ESO 2001