Magnetic fields in a static plasma of finite electric conductivity
![]() are subject to diffusion and dissipation, the timescale of
which is
are subject to diffusion and dissipation, the timescale of
which is
![]() (
(
![]() is
the magnetic diffusivity).
However, in a flowing plasma, magnetic fields may be created
with certain velocity fields. This is the so-called
"dynamo'' process, which converts kinetic energy into magnetic
energy (e.g., Moffatt 1978). The equation describing the
time-variation of the magnetic field
is
the magnetic diffusivity).
However, in a flowing plasma, magnetic fields may be created
with certain velocity fields. This is the so-called
"dynamo'' process, which converts kinetic energy into magnetic
energy (e.g., Moffatt 1978). The equation describing the
time-variation of the magnetic field ![]() governs the dynamo
action
governs the dynamo
action
Thompson & Duncan (TD93) concluded that the dominant kinetic energy to
be converted into magnetic energy in the dynamo action of PNSs is the
convective energy since the initial pulsar rotation period is probably
much larger than the overturn time (![]() 1 ms) of a convective cell,
although large-scale
1 ms) of a convective cell,
although large-scale
![]() dynamo action is essential for
neutron stars with
dynamo action is essential for
neutron stars with
![]() (i.e., initial period
(i.e., initial period
![]() 1 ms)
to produce very high fields ("magnetars'', Duncan & Thompson 1992).
However, here we suggest that rotation can not be neglected even for
pulsars with typical initial periods, because the differential rotation
energy density
1 ms)
to produce very high fields ("magnetars'', Duncan & Thompson 1992).
However, here we suggest that rotation can not be neglected even for
pulsars with typical initial periods, because the differential rotation
energy density
![]() erg cm-3is even larger than the turbulent energy density
erg cm-3is even larger than the turbulent energy density
![]() erg cm-3 for P=10 ms.
If the large-scale convection scenario discussed in Sect. 2.2
is possible, most of the differential rotation energy may be
converted to magnetic energy by dynamo action.
Let's first estimate the total
differential rotation energy
erg cm-3 for P=10 ms.
If the large-scale convection scenario discussed in Sect. 2.2
is possible, most of the differential rotation energy may be
converted to magnetic energy by dynamo action.
Let's first estimate the total
differential rotation energy ![]() in the case when the angular
momentum of each mass element is conserved in the collapse,
in the case when the angular
momentum of each mass element is conserved in the collapse,
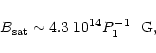 |
(38) |
In the other scenario, where diffusivities based on neutrino
scattering inhibit large-scale convection, the differential rotation
is damped due to the momentum transport by neutrinos.
In this case the dynamo may be
driven dominantly by turbulent convection, and the field strength
can be estimated as
![]() G,
assuming an equilibrium state between kinetic and magnetic energy.
The efficiency of converting differential rotation energy into
magnetic energy by dynamo action in this scenario may be much smaller
than in the case where convection with the large scale Lexists since a significant fraction of differential rotation energy is
likely to be converted into thermal energy due to the high neutrino
viscosity.
G,
assuming an equilibrium state between kinetic and magnetic energy.
The efficiency of converting differential rotation energy into
magnetic energy by dynamo action in this scenario may be much smaller
than in the case where convection with the large scale Lexists since a significant fraction of differential rotation energy is
likely to be converted into thermal energy due to the high neutrino
viscosity.
Thus, dynamo action may amplify significantly the field before PSSs
cools down to temperatures T smaller than the critical one,
![]() .
When
.
When
![]() ,
CSC appears, and the field would exist
as a fossil one for a very long time since
,
CSC appears, and the field would exist
as a fossil one for a very long time since
![]() if
if
![]() .
In fact, Alford et al. (2000) investigated recently the effect of CSC
on the magnetic fields, and found that, unlike the conventional
superconductors where weak magnetic fields are expelled by the Meissner
effect, color superconductors can be penetrated by external magnetic
fields and such fields can exist stably on a timescale longer than
the cosmic age.
.
In fact, Alford et al. (2000) investigated recently the effect of CSC
on the magnetic fields, and found that, unlike the conventional
superconductors where weak magnetic fields are expelled by the Meissner
effect, color superconductors can be penetrated by external magnetic
fields and such fields can exist stably on a timescale longer than
the cosmic age.
Equation (39) may have an observational consequence for pulsar
statistics, which in turn could test Eq. (39). In the
magnetic dipole model of pulsars,
![]() (note: fields are assumed not to
decay in SQM), and the rotation period P is a function of time
t due to energy loss. P(0) denotes the initial period of
pulsars. Considering Eq. (39), one has
(note: fields are assumed not to
decay in SQM), and the rotation period P is a function of time
t due to energy loss. P(0) denotes the initial period of
pulsars. Considering Eq. (39), one has
![]() ,
the solution of which is
,
the solution of which is
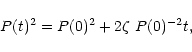 |
(40) |
The condition
![]() gives a limit for the initial
pulsar period P. Based on Eq. (37), one gets P>0.2 ms.
Actually,
gives a limit for the initial
pulsar period P. Based on Eq. (37), one gets P>0.2 ms.
Actually, ![]() ms since the efficiency of converting
gravitation energy into differential rotation energy during
collapse may be very small. It is thus doubtful that supernovae
can produce pulsars with submilliseconds periods.
For recycled millisecond pulsars the above estimate is not relevant.
ms since the efficiency of converting
gravitation energy into differential rotation energy during
collapse may be very small. It is thus doubtful that supernovae
can produce pulsars with submilliseconds periods.
For recycled millisecond pulsars the above estimate is not relevant.
The magnetic field amplification processes in newborn pulsars are
essentially fast dynamos because of the high magnetic Reynolds
numbers (
![]() for large-scale convection,
for large-scale convection,
![]() for local turbulence)
of both PSSs and PNSs.
Unfortunately, the question of whether or not fast dynamo exist has
not been answered theoretically although many numerical and analytical
calculations strongly support the existence of kinematic fast dynamos
for given sufficiently complicated flows (Soward 1994; Childress &
Gilbert 1995).
It is worth studying fluids without magnetic diffusion since the
diffusion timescale is much longer than the advection timescale,
for local turbulence)
of both PSSs and PNSs.
Unfortunately, the question of whether or not fast dynamo exist has
not been answered theoretically although many numerical and analytical
calculations strongly support the existence of kinematic fast dynamos
for given sufficiently complicated flows (Soward 1994; Childress &
Gilbert 1995).
It is worth studying fluids without magnetic diffusion since the
diffusion timescale is much longer than the advection timescale,
![]() ,
for fast dynamos. The complex
flows, such as stretch-twist-fold, may effectively amplify the
field in this case.
The amplified strong magnetic fields are concentrated in filaments
with radii
,
for fast dynamos. The complex
flows, such as stretch-twist-fold, may effectively amplify the
field in this case.
The amplified strong magnetic fields are concentrated in filaments
with radii ![]() ,
which can be estimated to be
,
which can be estimated to be
![]() mm (
mm (
![]() )
by equating
the diffusion timescale of filament field,
)
by equating
the diffusion timescale of filament field,
![]() ,
to the advection timescale
,
to the advection timescale
![]() .
Fast dynamos in PNSs have been considered by Thompson & Duncan
(TD93) who suggested PNS dynamos as the origins of pulsar magnetism.
As the fluid parameters (e.g.,
.
Fast dynamos in PNSs have been considered by Thompson & Duncan
(TD93) who suggested PNS dynamos as the origins of pulsar magnetism.
As the fluid parameters (e.g.,
![]() ,
,
![]() ,
,
![]() )
of
both PSSs and PNSs are similar, fast dynamos may also work for newborn
strange stars.
)
of
both PSSs and PNSs are similar, fast dynamos may also work for newborn
strange stars.
There are three timescales in the fast dynamo of PSSs: the diffuse
timescale
![]() ,
the advection
timescale
,
the advection
timescale
![]() ,
and the buoyancy
timescale
,
and the buoyancy
timescale
![]() ,
,
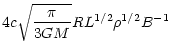 |
|||
| (41) |
Let's give some estimates for fast dynamos. There are mainly two
types of flows in PSSs: eddy (convection) and shear (differential
rotation). Actually, these flows are coupled. However, we may
deal with them separately in order to have an overview of the
field generation processes.
For pure straining motion with velocity field ![]() ,
,
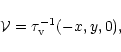 |
(42) |
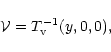 |
(43) |
Differential rotation may play an essential role for the
generation of large-scale magnetic fields through
![]() dynamo process, but even in the absence of differential rotation,
large-scale magnetic fields may be created. Owing to the alignment
of small-scale convection rolls parallel to the axis of rotation,
global magnetic fields can be generated as has been shown in
various dynamo models (see, for instance, Busse 1975).
dynamo process, but even in the absence of differential rotation,
large-scale magnetic fields may be created. Owing to the alignment
of small-scale convection rolls parallel to the axis of rotation,
global magnetic fields can be generated as has been shown in
various dynamo models (see, for instance, Busse 1975).
Copyright ESO 2001