The time-scale of PNSs (or PSSs) is of the order of a few seconds, which is three orders of magnitude longer than the dynamical one. It is thus worth studying the dynamical bulk evolution in these stars, such as differential rotation and convection. Unfortunately, no numerical model of supernova explosion known hitherto has included the conversion from PNSs to PSSs, although such a conversion may help in modelling the burst process (e.g., 1, helping to solve the present energetic difficulties in getting type II supernova explosions (Benvenuto & Horvath 1989); 2, giving a reasonable explanation for the second peak of neutrino emission in SN 1987A (Benvenuto & Lugones 1999)). The absence of a numerical model is caused by the lack of (1) a full theory determining the conditions at which the quark matter phase transition occurs and of (2) a detailed understanding of the complex burning process of neutron matter into strange matter.
Nevertheless, some efforts have been made in trying
to understand the transition and combustion processes in detail.
The phase conversion occurs in two steps: first neutron matter
deconfinement occurs on a strong interaction time scale ![]() 10-23 s, then chemical equilibration of the deconfined
quark matter takes place on a weak interaction time scale
10-23 s, then chemical equilibration of the deconfined
quark matter takes place on a weak interaction time scale ![]() 10-8 s. Additional neutrinos and energy are produced in
the second step (Dai et al. 1995). Further calculations of
such transitions (Anand et al. 1997; Lugones & Benvenuto 1998)
have also considered the effect of strong interactions, the
effect of finite temperature and strange quark mass, and the
effect of trapped neutrinos. Recently, Benvenuto & Lugones
(1999) explored the occurrence of deconfinement transition in a
PNS modeled by Keil & Janka (1995) and found that the
deconfinement appears as long as the bag constant
10-8 s. Additional neutrinos and energy are produced in
the second step (Dai et al. 1995). Further calculations of
such transitions (Anand et al. 1997; Lugones & Benvenuto 1998)
have also considered the effect of strong interactions, the
effect of finite temperature and strange quark mass, and the
effect of trapped neutrinos. Recently, Benvenuto & Lugones
(1999) explored the occurrence of deconfinement transition in a
PNS modeled by Keil & Janka (1995) and found that the
deconfinement appears as long as the bag constant
![]() 126 MeV fm-3. Various estimates of the bag constant
indicate that the preferred value of
126 MeV fm-3. Various estimates of the bag constant
indicate that the preferred value of
![]() lies in the
range of 60 MeV fm
lies in the
range of 60 MeV fm
![]() MeV fm-3 (Drago 1999), which means that deconfinement is
very likely to happen. Such 2-flavor quark matter may be
transformed immediately into a 3-flavor one if SQM is absolutely
stable.
From a kinetic point of view, Olinto (1987) has calculated
for the first time
the conversion of neutron stars into strange stars, suggesting
a deflagration mode with a burning velocity range from 104 kms-1to a few cm/s. However it is found (Horvath & Benvenuto 1988;
Benvenuto et al. 1989; Benvenuto & Horvath 1989)
that such slow modes are unstable. This instability would be
self-accelerated, and the burning should occur finally in
detonation modes, although the transition from deflagration to
detonation has not been well understood (Lugones et al. 1994).
In order for the combustion to be exothermic, there exists a
minimum density
MeV fm-3 (Drago 1999), which means that deconfinement is
very likely to happen. Such 2-flavor quark matter may be
transformed immediately into a 3-flavor one if SQM is absolutely
stable.
From a kinetic point of view, Olinto (1987) has calculated
for the first time
the conversion of neutron stars into strange stars, suggesting
a deflagration mode with a burning velocity range from 104 kms-1to a few cm/s. However it is found (Horvath & Benvenuto 1988;
Benvenuto et al. 1989; Benvenuto & Horvath 1989)
that such slow modes are unstable. This instability would be
self-accelerated, and the burning should occur finally in
detonation modes, although the transition from deflagration to
detonation has not been well understood (Lugones et al. 1994).
In order for the combustion to be exothermic, there exists a
minimum density
![]() for detonation to be possible,
for detonation to be possible,
![]() times of nuclear density for some cases
(Benvenuto & Horvath 1989). Thus the detonation flame can not
reach the edge of the compact core, and the outer part of the PNS
would be expelled. As a result, a strange star is formed with an
almost "bare'' quark surface which is essential to solve
completely the "binding energy'' problem in some current pulsar
emission models (Xu et al. 1999, 2001). Both the extra
neutrino emissivity and the detonation wave can favour a
successful core-collapse supernova explosion.
times of nuclear density for some cases
(Benvenuto & Horvath 1989). Thus the detonation flame can not
reach the edge of the compact core, and the outer part of the PNS
would be expelled. As a result, a strange star is formed with an
almost "bare'' quark surface which is essential to solve
completely the "binding energy'' problem in some current pulsar
emission models (Xu et al. 1999, 2001). Both the extra
neutrino emissivity and the detonation wave can favour a
successful core-collapse supernova explosion.
It is expected that PNSs (thus PSSs) have a strong differential
rotation (e.g., Janka & Mönchmeyer 1989; Goussard et al. 1998).
This issue is uncertain, however, due to the lack of a rotating
core model in the pre-supernova evolution simulations. The iron
core collapses, being triggered by electron capture (for lower
entropy core) and/or photodisintegration (for higher entropy
core), almost in the same way as for free fall. Many initial core
models of highly evolved massive stars without rotation have
appeared in the literature (e.g., Arnett 1977; Bruenn 1985), in
which the density ![]() - radius r0 relation can be fitted
by
- radius r0 relation can be fitted
by
Based on the approximation, the total rotational energy E0 of
the core is
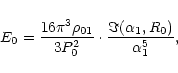 |
(3) |
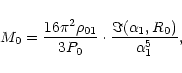 |
(4) |
| = | |||
| (5) |
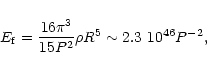 |
(8) |
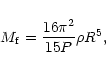 |
(9) |
Figure 1 shows the velocity and the velocity derivative
of this differential rotation scenario for P=10 ms,
respectively, based on Eq. (7) and Eq. (11). We find
![]() s-1 in the outer part of PNSs or PSSs.
Such differential rotation may play an important role in the
creation of magnetic fields of PSS or PNS, as will be discussed in
Sect. 3.
s-1 in the outer part of PNSs or PSSs.
Such differential rotation may play an important role in the
creation of magnetic fields of PSS or PNS, as will be discussed in
Sect. 3.
Since the dynamo actions are in the outer convective layer with
thickness
![]() cm (see Eq. (12) and
Sect. 3), we give the velocity difference of differential
rotation,
cm (see Eq. (12) and
Sect. 3), we give the velocity difference of differential
rotation,
![]() ,
as a function of P in Fig. 2.
,
as a function of P in Fig. 2.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{f2.eps} \end{figure}](/articles/aa/full/2001/21/aa10332/Timg60.gif) |
Figure 2:
The
velocity difference in the convective outer layer with thickness
of |
Turbulent convection in PNSs has been extensively investigated
before (e.g. Burrows & Lattimer 1988; Wilson & Mayle 1988;
Miralles et al. 2000). In the Kelvin-Helmholtz cooling
phase, both the negative gradient of the entropy and of the
lepton fraction can drive convection in newborn neutron stars,
given that the mean free paths of leptons are much smaller than
the convection length scale.
Protostrange stars form after the SQM phase-transition with a
time scale of
![]() s, which is much shorter
than that of neutrino diffusion and thermal evolution, assuming
that the actual combustion mode is detonation (Benvenuto et al. 1989).
s, which is much shorter
than that of neutrino diffusion and thermal evolution, assuming
that the actual combustion mode is detonation (Benvenuto et al. 1989).
We expect that PSSs are convective, since negative gradients of
entropy and neutrino fractions would also appear in the outermost
layers which can lose entropy and neutrinos faster than the inner
part. Following arguments used by Thompson & Duncan (TD93) in
the case of PNSs, we compare the radiative and adiabatic
temperature profiles to see whether convection occurs in PSSs. We
assume neutrinos in the outer part of PSS are nondegenerate since
there the neutrinos are lost rapidly. Iwamoto (1982) has shown
that for the mean free path l of the scattering of nondegenerate
neutrinos by relativistic degenerate quark matter with
temperature T,
![]() holds. Thus, the neutrino
opacity in SQM scales as T3 (rather than T2 as for the case
of PNSs), and the radiative temperature profile in PSSs is much
steeper,
holds. Thus, the neutrino
opacity in SQM scales as T3 (rather than T2 as for the case
of PNSs), and the radiative temperature profile in PSSs is much
steeper,
![]() .
We can employ the analytical
equation of state for SQM in the case of zero strange quark mass
(
.
We can employ the analytical
equation of state for SQM in the case of zero strange quark mass
(
![]() )
and zero coupling constant (
)
and zero coupling constant (
![]() )
of strong interaction (Cleymans et al. 1986; Benvenuto et al.
1989) to estimate the adiabatic temperature-pressure relation.
The entropy per baryon is
)
of strong interaction (Cleymans et al. 1986; Benvenuto et al.
1989) to estimate the adiabatic temperature-pressure relation.
The entropy per baryon is
![]() for the case of
chemical potential
for the case of
chemical potential
![]() MeV and temperature
MeV and temperature ![]() MeV. Therefore
MeV. Therefore
![]() for SQM moving
with fixed S is much less steep, and we can thus expect that a
negative entropy gradient appears in the outer layer which is
unstable to convection, similar to the case of PNSs.
Accordingly we suggest that Schwarzchild convection exists in
PSSs, whereas it will depend on detailed simulations whether
Ledoux convection in PSSs can
be established.
If the timescale
for SQM moving
with fixed S is much less steep, and we can thus expect that a
negative entropy gradient appears in the outer layer which is
unstable to convection, similar to the case of PNSs.
Accordingly we suggest that Schwarzchild convection exists in
PSSs, whereas it will depend on detailed simulations whether
Ledoux convection in PSSs can
be established.
If the timescale
![]() for neutron matter convection is
much smaller than the neutrino diffusion time (a few seconds), we
may expect that Ledoux convection takes place in a PSS since
the negative gradient of the lepton fraction is nearly the same
for PSSs as that for PNSs.
for neutron matter convection is
much smaller than the neutrino diffusion time (a few seconds), we
may expect that Ledoux convection takes place in a PSS since
the negative gradient of the lepton fraction is nearly the same
for PSSs as that for PNSs.
In the following, we try to estimate the properties of convection
in PSSs. The local pressure scale height ![]() in PSS is
in PSS is
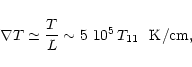 |
(13) |
There are two factors which can cause viscous stresses in a PSS:
neutrino transport and quark scattering.
Neutrino-induced viscosity dominates in a PSS on scales that are
large compared to the neutrino mean-free path l. We use the
neutrino mean-free path of nondegenerate neutrino scattering
in SQM for a dimensional estimate (Iwamoto 1982),
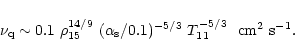 |
(18) |
Two possibilities arise for the scenario of turbulence in PSSs.
The first one is that the neutrino viscosity can effectively inhibit
a large-scale convection with length scale L, and local convection with
scale
![]() will exist.
In this case the local thermal diffusivity due to quark scattering
in SQM (Heiselberg & Pethick 1993) is
will exist.
In this case the local thermal diffusivity due to quark scattering
in SQM (Heiselberg & Pethick 1993) is
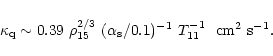 |
(19) |
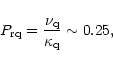 |
(20) |
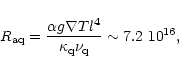 |
(21) |
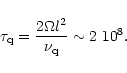 |
(22) |
The second scenario is that the neutrino viscosity is not high enough
to inhibit the large-scale convection, and convection with scale L is
possible.
We can also obtain some dimensionless numbers for this case.
Since both the thermal energy and momentum in PSSs are transported by
neutrinos now, the thermal diffusivity ![]() can be estimated to be
(Wilson & Mayle 1988)
can be estimated to be
(Wilson & Mayle 1988)
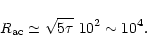 |
(29) |
Another cause of turbulent motion in PSS (and PNS) is differential
rotation.
The Reynolds number ![]() of this shear flow is
of this shear flow is
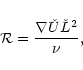 |
(32) |
Copyright ESO 2001