CCS is a linear radical whose electronic ground state is the
![]() configuration (Saito et al. 1987), i.e., the projection of the orbital
angular momentum onto the molecular axis vanishes,
configuration (Saito et al. 1987), i.e., the projection of the orbital
angular momentum onto the molecular axis vanishes, ![]() = 0, and spin
angular momentum S = 1. Since the electronic orbital angular momentum
= 0, and spin
angular momentum S = 1. Since the electronic orbital angular momentum
![]() is far more strongly coupled to the molecular axis than the spin
(at least for the slow molecular rotations considered here), the intrinsic
magnetic field due to the molecular rotation is expected to couple the spin
magnetic moment to the molecular axis. The limiting case is usually described
in terms of Hund's case b (e.g., Townes & Schawlow 1975).
In the case of CCS, however, the dipole-dipole interaction between the two
unpaired electrons is unusually large. For small rotational and projected
orbital angular momenta,
is far more strongly coupled to the molecular axis than the spin
(at least for the slow molecular rotations considered here), the intrinsic
magnetic field due to the molecular rotation is expected to couple the spin
magnetic moment to the molecular axis. The limiting case is usually described
in terms of Hund's case b (e.g., Townes & Schawlow 1975).
In the case of CCS, however, the dipole-dipole interaction between the two
unpaired electrons is unusually large. For small rotational and projected
orbital angular momenta, ![]() and
and
![]() ,
i.e., small
,
i.e., small ![]() (=
(= ![]() +
+
![]() ), the intrinsic magnetic field associated with
the molecular rotation becomes so small that the spin-spin interaction
dominates the coupling of the electronic spin onto the molecular axis. This
case is rather described by Hund's case a, where the total angular
momentum
), the intrinsic magnetic field associated with
the molecular rotation becomes so small that the spin-spin interaction
dominates the coupling of the electronic spin onto the molecular axis. This
case is rather described by Hund's case a, where the total angular
momentum ![]() results from the coupling of
results from the coupling of
![]() and
and ![]() ;
the angular momentum
;
the angular momentum
![]() is the projection of
is the projection of ![]() onto the
molecular axis, and, correspondingly,
onto the
molecular axis, and, correspondingly,
![]() is the projection of
is the projection of
![]() .
.
The energy associated with the magnetic dipole interaction of a paramagnetic
molecule with an external magnetic field ![]() is given by
is given by
where
![]() is the magnetic moment of the CCS radical in state
JN, associated with the total angular momentum operator
is the magnetic moment of the CCS radical in state
JN, associated with the total angular momentum operator ![]() ,
,
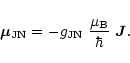 |
(A.1) |
Generally,
![]() results from individual contributions (e.g.,
Judd 1975),
results from individual contributions (e.g.,
Judd 1975),
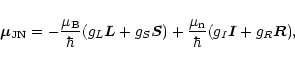
where
![]() is the Bohr magneton,
is the Bohr magneton,
![]() is the nuclear magneton,
is the nuclear magneton,
![]() is the nuclear spin,
is the nuclear spin, ![]() is the electronic orbital and
is the electronic orbital and
![]() the total orbital angular momentum. The g-factors are defined as
usual. For CCS in its ground state configuration the terms involving
the total orbital angular momentum. The g-factors are defined as
usual. For CCS in its ground state configuration the terms involving
![]() and
and ![]() can be neglected since
can be neglected since
![]() .
Therefore,
the magnetic moment
.
Therefore,
the magnetic moment
![]() can be expressed by
can be expressed by
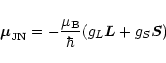 |
(A.2) |
to an excellent approximation. The JN = 01 level has a vanishing
magnetic moment because of J = 0. The rotational ground state can
thus not split into magnetic sublevels due to an external magnetic
field. Taking the quantization axis along the direction of ![]() the
splitting energy of other rotational levels JN due to the Zeeman effect
is given by
the
splitting energy of other rotational levels JN due to the Zeeman effect
is given by
| (A.3) |
where
![]() is the corresponding magnetic quantum number and B is the
magnetic field strength.
is the corresponding magnetic quantum number and B is the
magnetic field strength.
Since the lower rotational states can be approximated by Hund's case
a, we designate eigenvectors by
![]() >.
Because of S=1 and
>.
Because of S=1 and ![]() = 0 in the J = 1 state,
= 0 in the J = 1 state,
![]() +1, 0, -1, and
+1, 0, -1, and
![]()
![]() 0, 1.
Hence, there are three corresponding eigenvectors: |1111>, |0011>
and |-1111>.
0, 1.
Hence, there are three corresponding eigenvectors: |1111>, |0011>
and |-1111>.
For any linear molecule in the ![]() configuration, the Hamiltonian
is given by (Gordy & Cook 1984)
configuration, the Hamiltonian
is given by (Gordy & Cook 1984)
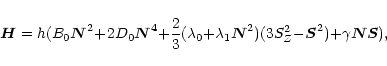
where (in the case of CCS) B0 (=6477.74952 MHz) is the rotation
constant, D0 (= 1.72704 kHz) is the centrifugal stretching,
![]() (= 97193.79 MHz) is the spin-spin coupling constant,
(= 97193.79 MHz) is the spin-spin coupling constant,
![]() (= 27.14 kHz) is the centrifugal correction, and
(= 27.14 kHz) is the centrifugal correction, and
![]() (= -14.645 MHz) is the spin-rotation coupling constant
(Saito et al. 1987).
(= -14.645 MHz) is the spin-rotation coupling constant
(Saito et al. 1987).
In order to express the above Hamiltonian in a form that is suitable for
case a eigenvectors, we notice that in case b
which is equivalent to
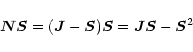
so that
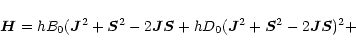
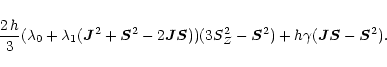
The operator product
![]() will be expressed in terms of the
ladder operators in order to apply eigenvalue equations later on,
will be expressed in terms of the
ladder operators in order to apply eigenvalue equations later on,
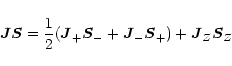 |
(A.4) |
using
The state vectors for ![]() can now be formed from linear combinations
of the eigenvectors,
can now be formed from linear combinations
of the eigenvectors,
![\begin{displaymath}\vert{\psi}_{n}{\makebox[1.5ex][l]{\hspace{-0.1ex}$>$ }} = {\...
...{\Sigma}{\Omega} S J{\makebox[1.5ex][l]{\hspace{-0.1ex}$>$ }}.
\end{displaymath}](/articles/aa/full/2001/19/aa10420/img148.gif) |
(A.5) |
For the solution of Schrödinger's equation,
![\begin{displaymath}\vec{H}\vert\psi_{n}{\makebox[1.5ex][l]{\hspace{-0.1ex}$>$ }}...
...E}_{n} \vert\psi_{n}{\makebox[1.5ex][l]{\hspace{-0.1ex}$>$ }},
\end{displaymath}](/articles/aa/full/2001/19/aa10420/img149.gif) |
(A.6) |
the following eigenvalue equations
have to be considered (e.g., Hougen 1970),
| = | (A.7) | ||
| = | (A.8) | ||
| = | (A.9) | ||
| = | (A.10) |
and
| = | (A.11) | ||
| = | (A.12) |
| = | (A.13) | ||
| = | (A.14) |
With those equations we obtain the matrix elements listed in Table A.1.
The solutions to Schrödinger's equation in matrix form
![\begin{displaymath}$<$\psi_{m}\vert\vec{H}\vert\psi_{n}{\makebox[1.5ex][l]{\hspace{-0.1ex}$>$ }} - {E}_{n} {\delta}_{mn} = 0
\end{displaymath}](/articles/aa/full/2001/19/aa10420/img166.gif) |
(A.15) |
can be found from the secular equation
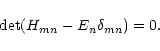
The solutions are the energy eigenvalues which correspond to three
energy levels in the J = 1 state, N = 0, 1, 2, as shown in
Fig. 2 of Saito et al. (1987),
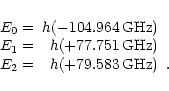
The smallest of those three energy eigenvalues corresponds to the energy
level
JN = 10.
|
<1111
| |
= |
|
| <1111
| |
= |
|
| <1111
|
|
= |
|
| <0011
| |
= |
|
| <0011
| |
= |
|
| <0011
| |
= |
|
| <
|
= |
|
| <
|
= |
|
| <
|
= |
|
In order to find the wavefunction for this energy eigenstate, the
coefficients c
![]() from the linear combination
(Eq. (A.5)) must be determined. Rewriting Eq. (A.5) as (omitting the
superscript 0 in the following)
from the linear combination
(Eq. (A.5)) must be determined. Rewriting Eq. (A.5) as (omitting the
superscript 0 in the following)
![\begin{displaymath}\vert{\psi}_{0}{\makebox[1.5ex][l]{\hspace{-0.1ex}$>$ }} = \l...
...array}{lll}
c_{-1} \\
c_{0} \\
c_{+1} \\
\end{array}\right)
\end{displaymath}](/articles/aa/full/2001/19/aa10420/img179.gif)
Eq. (A.15) yields
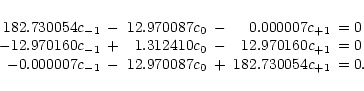
where the matrix elements in Table 1 were used. Both the first and third
equation give
c-1 = c+1, and consequently
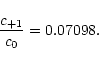
Hence the above system of equations is redundant, and a normalization is
introduced,
| c2-1 + c20 + c2+1 = 1, | (A.16) |
which allows to determine the individual coefficient to
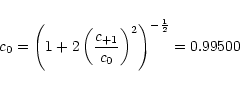
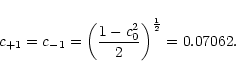
The wavefunction for the
JN = 10 level can now be given explicitely,
![\begin{displaymath}0.07062\,\vert 1111{\makebox[1.5ex][l]{\hspace{-0.1ex}$>$ }} ...
...\,\vert\mbox{--1111}{\makebox[1.5ex][l]{\hspace{-0.1ex}$>$ }}.
\end{displaymath}](/articles/aa/full/2001/19/aa10420/img185.gif)
In order to find the
![]() -factor for the JN = 10 level, Eqs. (A.1) and (A.2) were multiplied by
-factor for the JN = 10 level, Eqs. (A.1) and (A.2) were multiplied by ![]() to obtain
to obtain
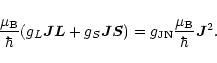
The corresponding expectation value in state
![]() is found by using
Eqs. (A.7) and (A.16),
is found by using
Eqs. (A.7) and (A.16),
![\begin{displaymath}{g}_{L} \, <{\psi}_{0}\vert \vec{J} \vec{L} \vert{\psi}_{0}{\...
...{S} \vert{\psi}_{0}{\makebox[1.5ex][l]{\hspace{-0.1ex}$>$ }} =
\end{displaymath}](/articles/aa/full/2001/19/aa10420/img189.gif)
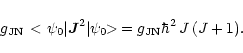
The evaluation of the expectation value for
![]() in state
in state
![]() requires eigenvalue equations for
requires eigenvalue equations for ![]() ,
,
![]() and
and ![]() .
In analogy to the eigenvalue equations for the spin
angular momentum, corresponding equations for the electronic orbital angular
momentum can be found substituting
.
In analogy to the eigenvalue equations for the spin
angular momentum, corresponding equations for the electronic orbital angular
momentum can be found substituting ![]() by
by ![]() ,
S by L and
,
S by L and
![]() by
by ![]() in Eqs. (A.7) through (A.14). (Hougen 1970).
Obviously, the operators
in Eqs. (A.7) through (A.14). (Hougen 1970).
Obviously, the operators
![]() and
and ![]() have non-vanishing
matrix elements only if the selection rule
have non-vanishing
matrix elements only if the selection rule
![]() =
= ![]() 1 is
satisfied, and
1 is
satisfied, and ![]()
![]() 0, respectively. Neither of these
requirements is fulfilled for the expectation value of
0, respectively. Neither of these
requirements is fulfilled for the expectation value of
![]() in state
in state
![]() ,
so that
<
,
so that
<
![]() = 0, hence
= 0, hence
![\begin{displaymath}{g}_{\rm JN} = \frac{{g}_{S}}{{J}~({J}\,+\,1)}~
\frac{1}{{\h...
...c{S} \vert{\psi}_{0}{\makebox[1.5ex][l]{\hspace{-0.1ex}$>$ }}.
\end{displaymath}](/articles/aa/full/2001/19/aa10420/img199.gif) |
(A.17) |
Using Eq. (A.4) and the eigenvalue Eqs. (A.9)-(A.14),
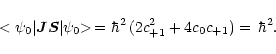
From Eq. (A.17) and recalling that
gS = 2.0023, the
![]() -factor for
JN = 10 level is finally determined to be
-factor for
JN = 10 level is finally determined to be
Copyright ESO 2001