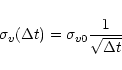 |
(8) |
| Doppler velocity error
|
||
| S-band | X-band | |
| Phase error | 1.0 mm/s | 0.3 mm/s |
| (thermal and ground | ||
| station contribution | ||
| Transponder quantisation | 0.4 mm/s | 0.1 mm/s |
| error in frequency | ||
| Transponder quantisation | 0.01 mm/s | 0.004 mm/s |
| error in phase | ||
| Total error (coherent mode) | 1.06 mm/s | 0.32 mm/s |
Another uncertainty which adds to the Doppler noise is the propagation of the radio signals through the turbulent solar wind (Bird 1982; Pätzold et al. 2000). Turbulent solar wind density variations along the radio ray path will induce dispersive carrier phase shifts on the radio carrier, increasing the phase noise. Using a dual-frequency downlink at S-band and X-band, it is possible to limit the solar wind noise by extracting the dispersive propagation contributions from the calculation of the differential Doppler and by correcting the X-band two-way radio link by this result.
At the time of the Siwa flyby (24th July 2008), the Siwa-Sun-Earth
angle is ![]() (Fig. 5). The impact parameter of the
radio ray path along the Earth-Siwa radius is about 191 solar radii still
close enough for contributions from the coronal plasma (solar wind) to the
radio link.
(Fig. 5). The impact parameter of the
radio ray path along the Earth-Siwa radius is about 191 solar radii still
close enough for contributions from the coronal plasma (solar wind) to the
radio link.
We estimate an enhancement of the Doppler noise by a factor of two with respect to the instrumental noise.
The integration time which will be used during the flybys are 600 s,
yielding a theoretical ![]() m/s rms noise figure for the Doppler velocity
from (8). The post-encounter Doppler velocity value for the
10 000 km distance in Fig. 2 is
m/s rms noise figure for the Doppler velocity
from (8). The post-encounter Doppler velocity value for the
10 000 km distance in Fig. 2 is ![]() m/s,
approximately four
m/s,
approximately four ![]() above Doppler noise level and therefore clearly
detectable assuming the increase in noise by a factor of two with respect to
(8) because of the propagation in the solar wind.
Anderson et al. (1992) estimated the fractional GM error as
above Doppler noise level and therefore clearly
detectable assuming the increase in noise by a factor of two with respect to
(8) because of the propagation in the solar wind.
Anderson et al. (1992) estimated the fractional GM error as
While the determination of the mass of Siwa from the RSI experiment is likely to have an accuracy of 1%, the estimate of the volume and hence the density will be much more inaccurate. The OSIRIS camera system on board Rosetta has avery high resolution of 60 m/px at closest approach. Thus, in two dimensions, OSIRIS will determine the cross-sectional area of the target to about 0.5%. However, the third dimension is unseen by the camera because it is unilluminated. Hence, this dimension can only be constrained from remote observations taken several hours before and using the asteroid's rotation. Even in this case, the rotation is unlikely to be orthogonal to the Sun-asteroid line (i.e. there is a constantly unilluminated pole). Thus, estimates, based on the asteroid having a reasonably continuous shape, have to be made. We estimate the resulting error to be of the order of 20% in both volume and density.
Copyright ESO 2001