

Up: Mass and density determinations
RSI will use the two-way radio carrier signals at X-band uplink (7168 MHz) and
S-band (2300 MHz) and X-band (8422 MHz) simultaneous downlink, provided by the
spacecraft radio subsystem, in order to measure slight changes in the
spacecraft velocity induced by the gravity attraction of the asteroid via the
classical Doppler effect.
If the spacecraft's velocity is changed by forces acting on the spacecraft,
a frequency shift of the radio carrier with respect to a predicted Doppler
shift (assuming no perturbing body present) is induced by
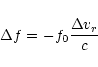 |
(1) |
where
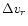 is the change of the spacecraft velocity along the
line-of-sight (LOS) caused by non-accounted forces acting on the spacecraft,
f0 is the radio carrier frequency at X-band and c is the speed of light.
If the two-way radio link is used as described above, the Doppler shift is
twice the value from (1).
is the change of the spacecraft velocity along the
line-of-sight (LOS) caused by non-accounted forces acting on the spacecraft,
f0 is the radio carrier frequency at X-band and c is the speed of light.
If the two-way radio link is used as described above, the Doppler shift is
twice the value from (1).
Table 1 gives the parameters for both flybys and
Fig. 1 sketches the flyby geometry for the Siwa case.
![\begin{figure}
\par\resizebox{12cm}{!}{\includegraphics{h2690_f1r.eps}}\hfill
\parbox[b]{55mm}{
}
\end{figure}](/articles/aa/full/2001/18/aah2690/Timg14.gif) |
Figure 1:
Rosetta flyby geometry at asteroid 140 Siwa on 24th July 2008.
The flyby plane contains the flyby trajectory (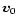 )
and the position
vectors from spacecraft to asteroid. The projected direction to the Earth forms
an angle of 174.04 )
and the position
vectors from spacecraft to asteroid. The projected direction to the Earth forms
an angle of 174.04 with the flyby trajectory. The direction to Earth
is located 3.35
with the flyby trajectory. The direction to Earth
is located 3.35 below the plane. The change in velocity
below the plane. The change in velocity
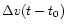 can be split in two components along the track
can be split in two components along the track
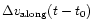 and across the track
and across the track
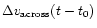 .
No net contribution to the total change in
velocity is gained from the .
No net contribution to the total change in
velocity is gained from the
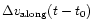 component.
Observed via the classical Doppler effect is
component.
Observed via the classical Doppler effect is
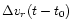 ,
the sum of ,
the sum of
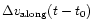 and
and
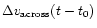 projected
onto the line-of-sight. The direction to the Sun lies in the flyby plane and
forms an angle of 167.61
projected
onto the line-of-sight. The direction to the Sun lies in the flyby plane and
forms an angle of 167.61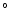 with
with 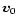 |
The flyby plane is defined as the plane containing the relative flyby velocity
vector (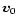 )
and the direction vectors relative to the asteroid. The
direction to the Sun lies also in this plane. During the flyby, the Rosetta
spacecraft will point the instrument panel toward the asteroid. The spacecraft
body will rotate during flyby in order to keep the remote sensing instruments
pointed towards the asteroid. The fully steerable HGA will remain pointed
toward the Earth which leads to a rotation of the HGA during flyby. A HGA
rotation end point will be reached about five minutes before encounter
resulting in the loss of radio signal. However, the instruments will remain
pointed by the on-going rotation of the spacecraft body. The spacecraft is
reoriented about 20 min after closest approach and spacecraft radio
tracking will proceed after reestablishing the two-way radio link.
The gravitational attraction from the asteroid acts onto the spacecraft at all
times along the flyby trajectory (Fig. 1) leading to
changes in the flyby velocity and trajectory. The deflection angle
)
and the direction vectors relative to the asteroid. The
direction to the Sun lies also in this plane. During the flyby, the Rosetta
spacecraft will point the instrument panel toward the asteroid. The spacecraft
body will rotate during flyby in order to keep the remote sensing instruments
pointed towards the asteroid. The fully steerable HGA will remain pointed
toward the Earth which leads to a rotation of the HGA during flyby. A HGA
rotation end point will be reached about five minutes before encounter
resulting in the loss of radio signal. However, the instruments will remain
pointed by the on-going rotation of the spacecraft body. The spacecraft is
reoriented about 20 min after closest approach and spacecraft radio
tracking will proceed after reestablishing the two-way radio link.
The gravitational attraction from the asteroid acts onto the spacecraft at all
times along the flyby trajectory (Fig. 1) leading to
changes in the flyby velocity and trajectory. The deflection angle 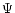 is
given by
is
given by
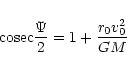 |
(2) |
(Danby 1992), where M = mass of the asteroid and G = gravitational
constant. For the nominal Siwa flyby at a closest approach distance of
r0=3500 km and relative flyby velocity v0=17.04 km s-1, this angle is
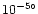 and the trajectory deflection can be neglected. Therefore,
we assume a straight flyby trajectory in the following with the radial
distance vector (spacecraft to Siwa) of
and the trajectory deflection can be neglected. Therefore,
we assume a straight flyby trajectory in the following with the radial
distance vector (spacecraft to Siwa) of
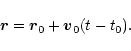 |
(3) |
The currently agreed nominal flyby distance of 3500 km is still subject to
discussion among the Rosetta instrument teams and may change in the future.
The smallest feasible flyby distance is 1750 km constrained by the maximum
slew rate of the spacecraft. It is not expected that a flyby distance larger
than 3500 km will finally be decided on.
Defining
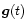 as the gravity attraction vector directed toward the
asteroid at time t
as the gravity attraction vector directed toward the
asteroid at time t
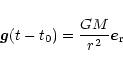 |
(4) |
where t0 = time of closest approach. The vector can be resolved into two
components along and across the trajectory direction. In the existing
literature (Anderson 1971; Anderson & Giampieri 1999; Rappaport et al. 2000)
this is accomplished by integration over time with initial conditions
at closest approach. Here, we choose to integrate with initial conditions at
 ,
which makes a small difference, equal to one-half of the total
deflection angle (2), in the direction of the two
components. The changes in velocity for both components because of the
gravitational attraction are:
,
which makes a small difference, equal to one-half of the total
deflection angle (2), in the direction of the two
components. The changes in velocity for both components because of the
gravitational attraction are:
Only the LOS components of these
velocity changes can be observed via the classical Doppler effect. Relevant is
the angle between the along-track direction and the projected LOS
(
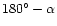 )
and the angle between the across-track direction and
the projected LOS (
)
and the angle between the across-track direction and
the projected LOS (
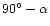 ). Furthermore the Earth is located
). Furthermore the Earth is located
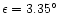 below the flyby plane. The total change in the Doppler
velocity along LOS due to gravity attraction during the flyby is then
below the flyby plane. The total change in the Doppler
velocity along LOS due to gravity attraction during the flyby is then
The RSI flyby strategy is twofold. First, by comparing the predicted "force-free''
pre-encounter Doppler frequency, gained from a precise orbit
determination after the last manoeuvre some days before the encounter, with
the actual observed Doppler frequency long after the closest approach but
before the first manoeuvre after the flyby. This procedure for detecting
velocity changes is similar to the one used for the Giotto flybys at comets
P/Halley and P/Grigg-Skjellerup (Pätzold et al. 1991a, 1991b, 1993). The
difference in Doppler frequency is translated into Doppler velocity along the
LOS via (1), taking into account that the two-way radio
link contributes twice the Doppler frequency value of (1),
and, from the encounter geometry (Fig. 1), the asteroid's
mass can be determined from the absolute values
Second, the real-time Doppler frequency is analysed during the flyby. Again,the Doppler velocity along the line-of-sight can be computed from
(1) at any time (t-t0). Figure 2
shows the theoretical Doppler velocity signature for three different closest
approach distances of 1750 km (the minimum feasible flyby distance), 3500 km
(the nominal closest approach distance) and 10 000 km for the Rosetta/Siwa
flyby.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{h2690_f2.eps}\hfill\parbox[b]{55mm}
{}
\end{figure}](/articles/aa/full/2001/18/aah2690/Timg39.gif) |
Figure 2:
Expected changes in velocity along the line-of-sight 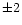 hours
about the time of closest approach to the asteroid Siwa for three different
flyby distances, 1750 km, 3500 km and 10 000 km
hours
about the time of closest approach to the asteroid Siwa for three different
flyby distances, 1750 km, 3500 km and 10 000 km |
Figure 3 shows simulated noisy Doppler velocity
measurements at 600 seconds integration time (solid circles) for the
nominal flyby distance of 3500 km.
Also included in the simulation is a gap of 25 min about
closest approach (grey area) lasting from 5 min before closest approach
to 20 min after closest approach due to the loss of the radio link.
A non-linear least squares fit according to Eqs. (3)
and (4) was applied to the simulated data points in order to
retrieve an estimate for GM of the asteroid.
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{h2690_f3.eps}\hfill\parbox[b]{55mm}
{}
\end{figure}](/articles/aa/full/2001/18/aah2690/Timg41.gif) |
Figure 3:
Simulated noisy Doppler velocity values for an integration time of
600 s (solid points) according to Eqs. (5)
and (6).
A random Gaussian distributed noise of
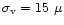 m/s was added
to each simulated data point plus an grossly overestimated contribution
of the same order of magnitude from the turbulent solar wind. The grey area
marks 20 min of expected loss of radio signal. The solid line is an
on-linear least squares fit to the simulated data points that yields GM as
a result to an accuracy of 1%. The same accuracy was estimated from
Anderson's (Anderson et al. 1992) rule of thumb (9) m/s was added
to each simulated data point plus an grossly overestimated contribution
of the same order of magnitude from the turbulent solar wind. The grey area
marks 20 min of expected loss of radio signal. The solid line is an
on-linear least squares fit to the simulated data points that yields GM as
a result to an accuracy of 1%. The same accuracy was estimated from
Anderson's (Anderson et al. 1992) rule of thumb (9) |


Up: Mass and density determinations
Copyright ESO 2001
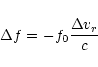
![]()
![]() )
and the direction vectors relative to the asteroid. The
direction to the Sun lies also in this plane. During the flyby, the Rosetta
spacecraft will point the instrument panel toward the asteroid. The spacecraft
body will rotate during flyby in order to keep the remote sensing instruments
pointed towards the asteroid. The fully steerable HGA will remain pointed
toward the Earth which leads to a rotation of the HGA during flyby. A HGA
rotation end point will be reached about five minutes before encounter
resulting in the loss of radio signal. However, the instruments will remain
pointed by the on-going rotation of the spacecraft body. The spacecraft is
reoriented about 20 min after closest approach and spacecraft radio
tracking will proceed after reestablishing the two-way radio link.
The gravitational attraction from the asteroid acts onto the spacecraft at all
times along the flyby trajectory (Fig. 1) leading to
changes in the flyby velocity and trajectory. The deflection angle
)
and the direction vectors relative to the asteroid. The
direction to the Sun lies also in this plane. During the flyby, the Rosetta
spacecraft will point the instrument panel toward the asteroid. The spacecraft
body will rotate during flyby in order to keep the remote sensing instruments
pointed towards the asteroid. The fully steerable HGA will remain pointed
toward the Earth which leads to a rotation of the HGA during flyby. A HGA
rotation end point will be reached about five minutes before encounter
resulting in the loss of radio signal. However, the instruments will remain
pointed by the on-going rotation of the spacecraft body. The spacecraft is
reoriented about 20 min after closest approach and spacecraft radio
tracking will proceed after reestablishing the two-way radio link.
The gravitational attraction from the asteroid acts onto the spacecraft at all
times along the flyby trajectory (Fig. 1) leading to
changes in the flyby velocity and trajectory. The deflection angle ![]() is
given by
is
given by
![]() as the gravity attraction vector directed toward the
asteroid at time t
as the gravity attraction vector directed toward the
asteroid at time t