3 Discussion

The good spatial and spectral resolution XMM-Newton data on 3C 58 has allowed us to perform a detailed spatially resolved spectral analysis of this remnant, and in particular, to address the topic of the spectra of the compact core at its center and the presence of an X-ray shell.

3.1 The compact core

The possible emission mechanisms for the compact core of 3C 58 have been reviewed by H95, and a preference has been given to a thermal model for the emission from hot polar caps, mostly on the basis of a review of ROSAT and Einstein HRI data. Torii et al. (2000) have confirmed the detection of an additional component in the remnant spectrum, which they have modeled with a black-body of kT=0.40-0.45 keV and a flux of 1.5 10³³D²_3.2 erg s^-1 in the 0.5-10 keV band. While the Torii et al. (2000) flux estimate is within 20% of the H95 one, we have found in ring 1 an upper limit to the flux of the kT=0.25 keV black-body component a factor of 10 less than the H95 estimate. The inferred upper limit on the emitting area is 1.3 10¹⁰ cm²(corresponding to a radius of $\sim$650 m), more or less the value found by Torii et al. (2000), and this is expected since our best-fit temperature is a factor of two less than the one derived by ASCA. By forcing the temperature at the value of Torii et al. (2000), the corresponding upper limits are 9.4 10^-14 erg cm^-2s^-1 ( $L_{\rm X}=1.1~10^{32}D^2_{3.2}$ erg s^-1) and 8 10⁸cm². While this large difference in the inferred black-body flux may seem puzzling, it may be explained by the dramatic improvement of the XMM-Newton spatial resolution compared with the ASCA one. In fact, if we compute the sum of our best-fit values for the flux of the black-body component of the pl+bbody fit over all the rings and the "edge" region, we obtain a 0.5-10 keV flux of 1.2 10^-12 erg cm^-2s^-1, or a luminosity of 1.3 10³³D²_3.2erg s^-1, in very good agreement with the value reported by H95 and Torii et al. (2000). More than 50% of this flux comes from ring 7-8 and the "edge" region: it is therefore probable that the ASCA data correctly detected a soft excess in the integrated spectrum of 3C 58, but this was incorrectly attributed to the thermal component of the central compact object, whereas Fig. 5 suggests that it comes from the external parts of the nebula. The more stringent XMM-Newton upper limit to the black-body component also heavily constrains its interpretation. Our value of the emission area is too low to assume that the whole surface of neutron star is loosing the residual heat of formation, and therefore would suggest the hot polar caps mechanisms. A review of the polar caps heating mechanisms can be found by Yancopoulos et al. (1994). H95 favors the "outer-gap" model, and in this case we expect $L_{\rm X}=10^{30}B_{12}P^{-2}$erg s^-1, where B₁₂ is the magnetic field in units of 10¹² G and P is the period in seconds. As shown in Fig. 6, our $L_{\rm X}$ upper limit yields a magnetic field higher than the highest value known for allowed B and P values of an 810 yr old pulsar. For this model to be compatible with the $L_{\rm X}$ upper limit, either an older pulsar must be present or, unlike the Crab, the pulsar has not suffered high energy losses, in which case all the points below the isochrone lines of Fig. 6 are allowed. Other mechanisms invoked to explain the hot polar caps yield estimates of $L_{\rm X}$ lower then the "outer-gap" model and in principle may be compatible with the observations. However, other observed pulsar nebulae-thermal pulsar pairs reported by Seward & Wang (1988) show a ratio between compact object luminosity and total (pulsar+nebula) luminosity $L_{\rm c}/L_{\rm tot}$ of $\sim$0.1-0.2 (the Crab has $L_{\rm c}/L_{\rm tot}=0.04$), while, using the observed total 3C 58 luminosity of 1.8 10³⁴ erg s^-1 and the upper limit we have derived, we derive a ratio <0.01. Figure 6 also shows that we expect a period less then 1 s for reasonable values of B, and therefore, to properly detect a pulsation, we would need a better time resolution than those of the EPIC camera in full image mode.

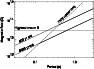Figure 6: The plot shows that allowed regions of the B-P plane according to the classical model for pulsars (e.g. Manchester & Taylor 1977) in solid lines (assuming the initial period was much less than the present period). We show the case for an 800 yr old pulsar (i.e. assuming that 3C 58 is related to SN 1181) and for a pulsar with an age a factor 10 larger. The dashed line represent the B-P values allowed by the "outer-gap" polar heated caps model of Cheng et al. (1986) and our derived upper limit to the black-body luminosity of the central source. The intersection of the observational and theoretical curves gives the allowed B-P values (thicker part of the isochrone lines). If 3C 58 is the remnant of SN 1181, the model would provide an unreasonably high B. Older pulsars and/or low rotational energy losses may yield more reasonable B values

3.2 Thermal emission at the edge of the nebula

The interpretation of the additional component in terms of expansion of the main shock in the environment of the SNR cannot be excluded a priori: recently, there have been some cases of SNRs reclassified as composite (e.g. G11.2-0.3, Vasisht et al. 1996; G327.1-1.1, Sun et al. 1999). The observed temperature of the MEKAL component corresponds to a shock speed of $\sim$450 kms^-1, while the emissivity corresponds to a post-shock density of $(0.60\pm 0.15)D_{3.2}^{-1/2}$ cm^-3 and a pre-shock density four times smaller (assuming the emission comes from a thin shell at $r=2.5\hbox{$^\prime$ }$, where the soft profile in Fig. 1 drops rapidly, and $\Delta r=r/12$). The emitting mass is of the order of 0.1 $D^{5/2}_{3.2}~M_\odot$. The inferred density is very reasonable for typical low galactic latitude Sedov SNRs, but on the other hand it can hardly be reconciled with the association between SN 1181 and 3C 58. This is shown in Fig. 7, which reports the allowed values of the SNR age and of the distance according to a simple Sedov analysis following the outline given in Kassim et al. (1993). It is clear that from a pure geometrical point of view, the measured X-ray temperature may represent a Sedov shock of an $\sim$800 yr old SNR located at a distance of 3.2 kpc ("Geom." solid line in Fig. 7), but the measured emission measure of the MEKAL component yields a solution with a distance well above 10 kpc and and a remnant age well in excess of $\sim$10⁴ yr, if we assume that the explosion energy is of the order of the "canonical" value 10⁵¹erg ( $\log E_{51}=0$ in Fig. 7, where E₅₁ is in units of 10⁵¹ erg). Among the lowest values of the explosion energy quoted in the literature, we have E₅₁=0.1 for Vela (Bocchino et al. 1999) and 0.02-0.3 for G292.0+1.8 (Hughes & Singh 1994), and we note that, for E₅₁=0.01, Fig. 7 gives a solution of a remnant at 8-10 kpc and an age of 3000-6000 yr. The association 3C 58-SN 1181 suggests an explosion energy of the order of 10⁴⁸ erg, roughly ten times lower than the lowest inferred. We recall that the association have been questioned by Huang (1986), but recently Stephenson & Green (1999) have pointed out that, on the basis of an update of historical information, the association should be reliable. If so, the Sedov model does not provide a proper description of all the observational evidence.

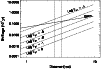Figure 7: Loci of allowed SNR age and distance according to a simple Sedov analysis of the thermal component of outer rim X-ray emission of 3C 58. The solid line labeled "Geom." gives the loci allowed by the simple geometrical relation between the real radius of the shell and the SNR age (Eq. (2) of Kassim et al. 1993). The radius is linked to the distance via the apparent shell radius, and we have used 2.5$^\prime$ to derive the relation. The dashed lines represent the loci of the solutions allowed by the Sedov relation R=14(E51/n0)1/5 t42/5, where n0 is derived from the emission measure of the MEKAL component assuming a spherical emitting volume with a radius of 2.5' and a filling factor of 25%. The intersection between the dashed lines and the solid line gives a solution. Vertical dashed lines mark the distance estimate of 2.6 and 3.2, due to Green & Gull (1982) and Roberts et al. (1993), respectively

In order to understand the interaction between 3C 58 and its environment, and to understand the origin of the soft X-ray component, it is useful to compare its radio and X-ray emission. The soft X-ray maps of Fig. 2 show that the X-ray emission is in any case confined within 2$^\prime$-4$^\prime$ from the center, and therefore the presence of the shell is in agreement with the lack of detection of a radio shell at $r>~5\hbox{$^\prime$ }$ of Reynolds & Aller (1985). It is interesting to note that there is a close correspondence between the radio morphology of the outer regions of the nebula and the soft X-ray maps (Fig. 2, upper panel). This is also observed in other shell-like young SNR like Kepler (Matsui et al. 1984) and Cas A (Keohane et al. 1996), while, on the other hand, the radio emission of the Crab nebula is four times greater than its X-ray counterpart. Reynolds & Aller (1988) have pointed out that the radio image of the remnant at 1446 MHz shows confined-edge emission at some locations of the outer regions of the nebula, and some of these also show limb-brightening. According to them, this may be explained if the edge of the nebula is sweeping up moving material, e.g. ejecta, like in the "inhomogeneous" model of Reynolds & Chevalier (1984), or the shock model invoked by Sankrit & Hester (1997) to explain the [O III] emission seen at the boundary of the Crab. This may explain the small amount of limb brightening and is also in agreement with the relatively slow shock speed measured in X-rays. In fact, the expected shock speed in the moving ejecta material is $\sim$300 kms^-1(Reynolds & Chevalier 1984; 150-200 km s^-1 in the Crab according to Sankrit & Hester 1997), and we observe $v_{\rm s}=450$ kms^-1. Therefore, the thermal component we observe in the outer rim of 3C 58 may be associated with the expansion of the nebula in the inner ejecta core. Note that this is also in agreement with the discrepancy between the large speed measured in 3C 58 filaments ($\sim$900 kms^-1, Fesen 1983) and the X-ray derived speed. In fact, the filaments are composed of material ejected in the explosion itself, pushed on and accelerated by the synchrotron nebula, while the X-ray emission is due a shock expanding into moving ejecta. However, the low value of the X-ray emitting mass would imply that the interaction is only at its beginning.

Finally, it should be noted that the above conclusions rely on the hypothesis of fast electron-ion equipartition. Unfortunately, it is not possible to independently measure the proton temperature $T_{\rm p}$ of the 3C 58 shock. Bocchino et al. (1999) have shown that $T_{\rm e} < T_{\rm p} < 2T_{\rm e}$ for a shock region of the old Vela SNR, but Hughes et al. (2000) found evidence for $T_{\rm p}\sim 45 T_{\rm e}$ in the 1000 yr old SNR E0102.2-7219, suggesting that non-equipartition may be common among young SNRs. If also in case of 3C 58 $T_{\rm p}$ is $\sim$45 times higher than the X-ray derived electron temperature, than a Sedov solution with $E_0 \sim 3~10^{49}$ erg, would be compatible with a distance of 3.2 kpc and the association with SN 1181.