2 Data analysis

2.1 Observations

Figure 1: MOS1+2 source profile, centered at $2^{\rm h}05^{\rm m}38.0^{\rm s} +64^{\rm d}49^{\rm m}37^{\rm s}$ (J2000). Soft, medium and hard energy band as defined in Fig. 2 are represented as tick marked top, medium and bottom curves, respectively. The solid black line is the Point Spread Function (PSF) of the mirror module 3 at 1.5 keV (Aschenbach et al. 2000)

Figure 2: MOS1+2 images binned at pixels of $2\hbox {$^{\prime \prime }$ }$ and smoothed using a Gaussian with $\sigma =3$ pixel to enhance the morphology of the faint nebula edge. Upper panel: soft image (0.1-1.0 keV). Center panel: medium energy image (1.0-2.0 keV). Lower panel: hard image (2.0-10.0 keV). Overlaid are contours representing the weakest ( $3\sigma =0.15$ Jy beam-1) 1446 MHz radio contour and the one corresponding to a flux density 4 times higher (both in white, from Reynolds & Aller 1988), and six X-ray contours (in yellow, from 1/100 of the peak to the peak value, logarithmically spaced)

3C 58 has been observed as part of the Cal/PV phase of the XMM-Newton satellite (Jansen et al. 2000). In this paper, we focus on the 25 ks on-axis observation performed during orbit 47, on March 12th 2000. Data from the two MOS (Turner et al. 2000) cameras and the PN (Strueder et al. 2000) camera have been used. MOS and PN cameras are CCD arrays which collect X-ray photons between 0.1 and 15 keV and have a field of view of $30^\prime$. The pixel size is $1.1\hbox{$^{\prime\prime}$ }$ and $4.1\hbox{$^{\prime\prime}$ }$ for MOS and PN respectively, and this should be compared with the mirror PSF width of $6\hbox{$^{\prime\prime}$ }{-}15\hbox{$^{\prime\prime}$ }$ FWHM-HEW. The data have been acquired with the medium filter and in full image mode, and therefore the temporal resolution is low, 2.5 s and 73 ms for MOS and PN, respectively. The worse spatial resolution of the PN is compensated by its greater sensitivity, on the average 20-30% more than the combined two MOS.

The Standard Analysis System (SAS) software we have used (version 5.0 alpha, xmmsas-20001011-1559) takes care of most of the required events screening. However, we have further screened the data to eliminate some residual hot pixels and occasional background enhancement due to intense flux of soft protons in the magnetosphere. In particular, we have extracted the background light-curve from a region free of sources, and we have identified time intervals of unusually high count rates (more than twice the "quiescent" background rate) and removed them from subsequent analysis. Moreover we have also selected events with value of the PATTERN pipeline assigned keywords between 0 and 12. The exposure time of the screened observations is 16 ks for the MOS and 12 ks for the PN detectors.

2.2 X-ray morphology

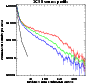
In Fig. 1, we report the 3C 58 profile as seen by the MOS1+2 computed in 65 annuli with $\Delta r = 4\hbox{$^{\prime\prime}$ }$ up to a distance of $\sim$ $4\hbox{$^\prime$ }$ from the centroid, located at $2^{\rm h}05^{\rm m}38.0^{\rm s} +64^{\rm d}49^{\rm m}37^{\rm s}$ (J2000, $\pm 1\hbox{$^{\prime\prime}$ }$). The background was collected from a ring with $\Delta r = 30\hbox{$^{\prime\prime}$ }$located at $4.5\hbox{$^\prime$ }$ from the center, and has been chosen to fall entirely in the central MOS chip. The comparison with the expected mirror PSF, also shown in Fig. 1 indicates that the central source is extended. The bright core region can be defined up to $\sim$ $50\hbox{$^{\prime\prime}$ }$ from the center; Further out, the slope changes and the behavior of the soft curve and hard curve is different. The hard curve declines with the same slope down to the limit of the radio nebula at $\sim$ $200\hbox{$^{\prime\prime}$ }$, while the soft curve is clearly flatter than the hard one, with a sudden change of slope occurring at $140\hbox{$^{\prime\prime}$ }$.

Figure 3: Spatially resolved spectral analysis with a power-law model of the X-ray nebula associated with 3C 58. We show the results obtained on the 8 annuli and the "edge" regions (the last point) as defined in the text. Black is MOS, red is PN, dotted bars are fit with free $N_{\rm H}$, solid bars are fit with $N_{\rm H}$ fixed at 4 1021 cm-2. Regions are centered at $2^{\rm h}05^{\rm m}38.0^{\rm s}$ $+64^{\rm d}49^{\rm m}37^{\rm s}$ (J2000). A linear fit to the MOS points corresponding to fits with $N_{\rm H}$ fixed at 4 1021 cm-2 is shown in the lower panel

The core is elongated in the N-S direction, with a FWHM of $13.5\pm 1.5\hbox{$^{\prime\prime}$ }$ in this direction ( $9.0\pm1.5\hbox{$^{\prime\prime}$ }$ in the E-W direction), in agreement with the ROSAT HRI results presented by H95. The centroid of the MOS1 emission is located 4 $^{\prime\prime}$ and 8 $^{\prime\prime}$ south of the ROSAT and Einstein positions. The data confirm that the radio wisp observed by Frail & Moffett (1993) is located to the East of the X-ray peak, at 5 $^{\prime\prime}$ from the the MOS1 centroid. However, the uncertainties in real attitude reconstruction, which is still not fully implemented, may give an uncertainty in absolute position determination as large as $\sim$ $5\hbox{$^{\prime\prime}$ }$.

Figure 2 shows the summed MOS1+2 images of 3C 58 in three different bands, namely 0.1-1 keV, 1-2 keV and 2-10 keV bands, along with the weakest 1446 MHz radio contour at 0.15 Jy beam^-1 and the contour at 0.6 Jy beam^-1 of Fig. 3 in Reynolds & Aller (1988) (both in white in Fig. 2). A small separation of the two contours (e.g. in the SW) indicates limb brightening and therefore confinement in the source. In addition, we also shown the X-ray contours (in yellow), and it is clear that there is correspondence between the radio contours and the X-ray emission of the soft image. In particular, the weakest radio contour matches the outer edge of the weak extended X-ray emission, especially at the north and south edges. Figure 2 also shows that the size of the nebula decreases as the energy increases, an effect also reported by Torii et al. (2000).

2.3 Spectral analysis

The high spatial and spectral resolution of the instrumentation aboard the XMM-Newton satellite allows us for the first time to perform spatially resolved spectral analysis of the X-ray nebula associated to 3C 58. To this end, we extracted spectra from 8 concentric annuli with $\Delta r = 8\hbox{$^{\prime\prime}$ }$ centered at the same position of the X-ray profiles of Fig. 1, covering the core emission up to 1.1$^\prime$ from the center. Given the uncertainties in present calibration of the MOS and PN cameras, and the energy dependence of the vignetting correction above 5 keV, we have restricted our spectral analysis to photons in the 0.5-5 keV energy band. The spectra have been background subtracted using the same background region introduced in the previous subsection, and have been rebinned to ensure that a minimum of 30 counts are present in each energy channel. As for response matrices and effective area files, we have used the latest version of standard MOS and PN matrices provided by the calibration team (mos1_medium_all_qe17_rmf3_tel5_15 and epn_fs20_sY9_medium). We have summed the spectra extracted with MOS1 and MOS2, and we have also rescaled the response matrix to reflect this operation. Besides the 8 annuli, we have also defined a region (the "edge'' region hereafter), represented by the union of two ellipses matching the outer X-ray edge of the nebula, minus a circle with same radius as the 8th annulus. This region is particularly suited for the study of the X-ray emission coming from the outermost fringes of the X-ray and radio nebula.

We have used three different emission models to fit the 3C 58 data, namely a power-law model, a power-law model plus the optically thin plasma model of Mewe et al. (1985) with Fe L calculation of Liedahl et al. (1995), pl+ MEKAL hereafter, and a power-law model plus a black-body spectrum, pl+bbody hereafter. These three models encompass what we could possibly expect from an X-ray nebula, the last two representing eventual contributions from a thermal shell (as in the case of known plerion-composite SNR), and from a compact source in the center as pointed out by Helfand et al. (1995). The temperature of the pl+ MEKAL model and of the pl+bbody models have been constrained in the 0.1-10 keV and in the 0.1-2.0 keV, respectively. Abundances are those of Anders & Grevesse (1989). All the models have been modified by the interstellar absorption according to cross-sections of Morrison & McCammon (1983), where we have let the equivalent hydrogen column density $N_{\rm H}$ vary. Since we have noted that the non-thermal component provides most of the flux in the XMM-Newton bandwidth, and that the residual thermal components of the model pl+ MEKAL and pl+bbody are correlated with the value of $N_{\rm H}$, we have also performed a set of fittings fixing the $N_{\rm H}$ value to 4 10²¹ cm^-2, which is compatible with previous estimates (Helfand et al. 1995; Torii et al. 2000) and it is also consistent with the result we obtained letting it vary.

 

 

Table 1: Goodness of MOS fits to the 8 annuli of 3C 58. The absorption is fixed to 4 10²¹ cm^-2. For each model, we report the value of $\chi ^2$, degrees of freedom (dof), null hypothesis probability. For the pl+ MEKAL and pl+bbody model, we also report the value of the best-fit temperature. The last column is the unabsorbed flux in the 0.5-10.0 keV in units of 10^-13 erg cm^-2 s^-1; its statistical error is $\pm 0.1$

Reg.	Power-law		Pow+ MEKAL			Pow+bbody
	$\chi^2/{\rm dof}$	Prob.	kT	$\chi^2/{\rm dof}$	Prob.	kT	$\chi^2/{\rm dof}$	Prob.	flux
1	74/73	46	1.0(>0.4)	71/71	48	0.2(>0.1)	73/71	40	15.3
2	69/65	35	6.0(>0.1)	67/63	35	0.9(>0.1)	68/63	30	13.0
3	65/63	41	0.6(>0.1)	65/61	34	$0.5\pm0.3$	62/61	44	11.4
4	52/59	71	0.1(>0.1)	51/57	70	0.1(>0.1)	51/57	69	12.3
5	54/61	72	0.7(>0.1)	52/59	72	0.2(>0.1)	53/59	69	12.0
6	52/59	74	0.1(>0.1)	50/57	72	0.6(>0.1)	50/57	72	10.9
7	96/60	0.2	0.2(<0.25)	91/58	0.4	0.8+0.2-0.1	91/58	0.4	10.7
8	79/58	3	0.3+0.2-0.1	71/56	8	0.8+0.3-0.1	73/56	7	10.6

2.3.1 The $\mathsfsl{\gamma}$ vs. radius relation

Figure 3 shows the best-fit value of the absorption and of the power-law photon index ($\gamma$) as a function of the distance from remnant center, obtained with a fit to a power-law emission model only. The data clearly show the effect of synchrotron burn-off of high energy electrons as the radius increases. This effect has also been observed in G21.5-0.9 both with Chandra (Slane et al. 2000) and XMM-Newton (Warwick et al. 2000) and it is related to inhomogeneity in the particle distribution inside the plerion nebula. The straight line in the lower panel of Fig. 3 represents the linear best-fit to the $\gamma - r$ relation, $\gamma=A+Br$ with $A=1.97\pm 0.03$ and $B=8.0\pm 0.6~10^{-3}$and r is in arcseconds. The MOS fits to the single power-law reported in Fig. 3 are statistically acceptable from ring 1 to ring 6, while not acceptable in rings 7-8 and in "the edge" region. This is true for both $N_{\rm H}$ free and $N_{\rm H}$ fixed fits, and Table 1 reports the $\chi^2/{\rm dof}$ values of the fits. It is interesting to note that the $N_{\rm H}$ value, when left free to vary, is significantly lower than the average value of 4 10²¹ cm^-2 for the outer nebula regions (Fig. 3). Moreover, the best-fit $\gamma$ of the shell is off the trend dictated by fit to the spectra of the rings when $N_{\rm H}$ is left free to vary, while it shows lower deviation in the fit with $N_{\rm H}$fixed. If the X-ray emission of the outer rings is dominated by the non-thermal component of the plerion, we do not expect significative variation of the absorption, and the data seem to confirm that a fixed $N_{\rm H}$ may be more appropriate. However, the fact that fits of the outer rings and "edge'' data are less acceptable than fits to inner rings data strongly suggests a contribution from other components.

2.3.2 Additional thermal components

Figure 4: A close up of MOS spectrum for the "edge'' region. Left panel: the fit with a simple power-law model does not well represent the spectrum below 1 keV. Center panel: the pl+ MEKAL model with kT=0.2 keV improves the description of the data. The spectral region near the oxygen edge (between 0.4 and 0.6) is know to have some residual calibration problem. Right panel: unfolded best-fit pl+ MEKAL model. Dot-dashed line represents the thermal component, which shows emission lines and falls off rapidly above 1 keV, where the power-law component dominates

In order to assess the presence of any additional emission from a central compact source (as suggested by H95) and from any thermal shell, we now consider the results of fits with pl+ MEKAL and pl+bbody models. The inclusion of the additional component ( MEKAL or bbody) does not increase the null hypothesis probability above 5%, except for ring 8. This is also reported in Table 1, in which the reader finds the data needed to evaluate the goodness of the fits we have performed. However, it should be noted that the inclusion of the MEKAL component leads to a reduction of $\chi ^2$ (and therefore to a better fit in a relative way) for the outermost rings, and a dramatic reduction in case of the "edge" region, specially for MOS. This is also shown in Fig. 4, where we show the MOS "edge" spectrum along with its power-law only and pl+ MEKAL best-fit model and residuals, and in Table 2 where we summarize the results of spectral fitting to the "edge" spectrum. In Fig. 5, we report the ratio of the flux of the second component ( $f_{\rm mekal}$ from the pl+ MEKAL fit in the upper panel, and $f_{\rm bbody}$ from the pl+bbody fit in the lower panel) to the total flux of ring 1-8 and the "edge" region.

The fit with an additional black-body component to ring 1 places an upper limit to the unabsorbed flux due to this component of 20% of the total 0.5-2.0 keV flux in this region (i.e. 1.5 10^-13 erg cm^-2s^-1, or a luminosity $L_{\rm X}=1.8~10^{32}D^2_{3.2}$ ergs^-1, where D_3.2 is the distance in units of 3.2 kpc, which is the most reliable value according to Roberts et al. 1993) and 10% of the total 0.5-10.0 keV flux of this region (i.e. 1.6 10^-13 erg cm^-2s^-1, same $L_{\rm X}$ as before). Since the whole remnant 0.5-10 keV flux is 1.6 10^-11 erg cm^-2s^-1, the upper limit corresponds to 1% of the remnant flux, significantly below the 7% found by Torii et al. (2000). Figure 5 also shows that spectral fittings of rings 2-6 yields only upper-limits to the presence of an additional MEKAL or black-body thermal emission.

On the other hand, the situation is different for ring 8 and the "edge" region (Tables 1 and 2), where the addition of the thermal component yields a significant decrement of the $\chi ^2$ (according to an F-test) and the thermal flux contribution to the 0.5-2.0 total flux is between 5% and 30%. In particular, the pl+ MEKAL fit in the "edge" region suggests that between 10 and 20% of the 0.5-2.0 keV flux from this region ( 5-9 10^-13 erg cm^-2s^-1, or $L_{\rm X}=5.8-10.0~10^{32}D^2_{3.2}$ ergs^-1) is due to the thermal component (8-14% if we consider the 0.5-10 keV band). If compared to the whole remnant 0.5-10 keV flux, the thermal soft excess yields a contribution of 3%-6%. It is important to note that in this region the pl+ MEKAL model is to be preferred over the pl+bbody model (Table 2).

 

 

Table 2: PN and MOS fit results of the "edge" region of 3C 58. All the fits yield an absorbed flux of 6.1 10^-12 erg cm^-2s^-1 in the 0.5-10 keV band

Model	$N_{\rm H}$	$\gamma$	kT	$\chi^2/{\rm dof}$
	cm-2		keV
MOS1+2
pow-law	$3.5\pm 0.2$	$2.61\pm 0.06$	-	245/170
pl+ MEKAL	7.3+0.6-0.9	$2.89\pm 0.08$	$0.18\pm 0.01$	202/168
pl+bbody	5.5+0.5-0.8	$2.75\pm 0.06$	<0.11	231/168
pow-law	4.0	$2.75\pm 0.04$	-	261/171
pl+ MEKAL	4.0	$2.61\pm 0.05$	$0.25\pm 0.03$	226/169
pl+bbody	4.0	$3.07\pm 0.07$	$0.78\pm 0.08$	243/169
PN
pow-law	$3.1\pm 0.3$	$2.42\pm 0.11$	-	113/138
pl+ MEKAL	7.6+0.4-2.5	2.71+0.15-0.11	$0.18\pm 0.03$	107/136
pl+bbody	5.2+1.0-1.7	2.55+0.11-0.16	<0.13	109/136
pow-law	4.0	$2.66\pm 0.06$	-	130/139
pl+ MEKAL	4.0	$2.47\pm 0.10$	$0.24\pm 0.06$	110/137
pl+bbody	4.0	$2.46\pm0.10$	<0.13	110/136

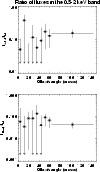Figure 5: Same as in Fig. 3, but here we report the ratio between the 0.5-2.0 keV flux due to the additional component ( MEKAL in the upper panel, and bbody in the lower panel) to the total 0.5-2.0 keV flux versus the distance from the center. Arrows indicate upper limits. Goodness of fits are reported in Table 1

2.3.3 PSF effects

We have also investigated whether our results are affected by any effect related to the Point Spread Function (PSF) of the XMM-Newton mirror. Since only 55% of the photons of a point source are contained within a circle of 8 $^{\prime\prime}$ radius, we expect a certain amount of scattering outside the rings. However, this effect is not likely to modify our conclusions. In the central ring, for instance, the strongly peaked morphology keeps the contamination from ring 2 low. Moreover, the scattering can only smooth the $\gamma - r$ relation in Fig. 3, so the observed slope is, strictly speaking, a lower limit to the real slope. Finally, in order to verify whether the soft component detected at large radii is an artifact of the PSF, we have followed this procedure: we have fitted the summed spectrum of rings 1-8 with a power-law model, and we have found $N_{\rm H}=3.9~10^{21}$ cm^-2 and $\gamma=2.21$; then, we have fitted the spectrum of the "edge" region with the best-fit model found for ring 1-8 with fixed $N_{\rm H}$ and $\gamma$, plus a second absorbed power-law model with free $N_{\rm H}$ and $\gamma$. The normalizations of the two models were left free to vary. We have found that the best-fit normalization of the "fixed" power-law is zero, suggesting that negligible contamination from the spectrum of the ring 1-8 is observed in the "edge" spectrum.

2.4 Timing analysis

In order to search pulsed X-ray emission from the central source which is powering 3C 58, we have calculated the power spectrum density of the time series of events of the central ring used for spectral analysis. Unfortunately, the time resolution of the EPIC cameras when operated in full image mode is low, and we were not able to sample frequencies above 1 Hz. For timing analysis, we have collected MOS1 and PN photons in ring 1 between 0.5 and 10 keV, and we have analyzed the two independently. Furthermore, we have also analyzed a more restricted energy range, 2-10 keV.

None of the power spectra show features significant at the 99% confidence level. The corresponding MOS1 upper limits to relative amplitude of a sinusoidal pulsed signal in the 5 10^-3-0.1 Hz is 6.2% and 10.0% for the 0.5-10 keV and 2-10 keV respectively, while the PN upper limits in the 10^-2-1 Hz are 2.0% and 3.1% in the broad and hard band, respectively.