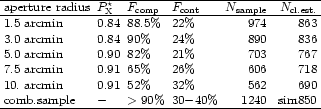
In total 452 stars with clearly visible diffraction spikes, 32 nearby galaxies, and 204 redundant detections of diffuse X-ray sources were removed from the sample. With the cleaned sample we can now repeat the statistical analysis with results given in Table 4. The sample selection cut is kept the same as above. (Note that in this statistics there are about 8% of the sources missing which leads to a lower normalization but has no effect on the conclusions drawn in the following). We note that this time the statistics indicates a number of about 800-900 for the expected number of clusters in the sample which is close to our expectations based on a comparison with cluster number counts found in deeper surveys (e.g. Gioia et al. 1990; Rosati 1998) as discussed in Sect. 2. We also note, that for the combined sample of candidates from the different aperture sizes, we obtain a total sample size which is about a factor of $\sim$ 1.5 larger than the estimated number of true clusters. Thus we expect a level of contamination of non-cluster sources around $30{-}40\%$ . This implies a laborious further identification work to clean the sample from the contamination, a price to be paid for the high completeness level aimed for.

**Table 4:** Statistics of the results of the galaxy counts around the X-ray sources in the sample cleaned from bright stars and multiple detections. The columns are as in Table 4
$\begin{table} \par $ \begin{array}{llllrr} \hline {\rm aperture~ radius}... ...0\% & 30{-}40\% & 1240 & $ sim$850\\ \hline \end{array} $\space \end{table}$

6.1 Comparison of the cluster search statistics with the final results of the REFLEX Survey

To analyse how well the cluster selection has worked we anticipate the results of the REFLEX survey and the final identification of the cluster candidates. We repeat the statistical analysis including all the sources from the starting sample with a flux in excess of 3 10^-12 ergs^-1 cm^-2, corresponding to the flux limit of the REFLEX sample (1417 sources without the multiple detections) except for the stars with diffraction spikes, and the nearby galaxies (1169 X-ray sources). The results of the cluster search for this high-flux sample (with the same values for the selection parameter, $P_{\rm X}^{\star}$ as used before) and the comparison with the final REFLEX sample is given in Table 5.

**Table 5:** Cluster search statistics for X-ray sources above a flux limit of 3 10^-12 erg s^-1 cm^-2 and comparison with the final REFLEX sample. The first 6 columns are as in Table 4. Column 7 gives the number of REFLEX cluster detected by the specific aperture search, Col. 8 the fraction detected compared to the total REFLEX sample, and Col. 9 the contamination fraction found in the candidate sample selected by the specific aperture
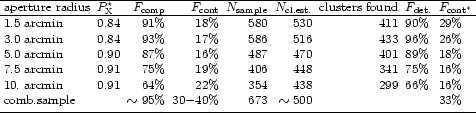$\begin{table} \par$% \begin{array}{llrrrrrll} \hline {\rm aperture~ radius}&... ...& & & 33\%\\ \noalign{\smallskip } \hline \end{array} $\space \end{table}$

We note from the results given in Table 5 that the predictions are very close to the actual findings. One has to be careful, however, in the interpretation of this comparison. In fact the general agreement should not be surprising as we have used the same statistics to select the sample and we have not yet used any independent means to include clusters missed by our search to check the incompleteness independently. Nevertheless a few results are striking. The number of clusters predicted to be found is close to the number actually identified. This shows that the signal observed in the diagnostic plots of the type of Fig. 12 is indeed due to galaxy clusters and there is no large contamination by other objects. Had we found for example much less clusters than predicted, we would be forced to speculate on the presence of another source population that mimics clusters in our analysis. This is obviously not the case and the high $P_{\rm X}(N)$ signal is correctly representing the clusters in the REFLEX sample. Also the trend in the efficiency of the different apertures in finding the clusters is predicted roughly correctly. There are only small differences, as for example that the total number of clusters and the contamination predicted from the results of the first two apertures are too high and too low, respectively.

Most of the clusters identified in the REFLEX survey (96%) are detected in the search with aperture 2 with a radius of 3 arcmin. That this ring size is the most effective is also shown in Fig. 13 where we compare the distribution of the probability values $P_{\rm X}(N)$ for the source sample and for the subsample which was identified as clusters in the course of the REFLEX Survey. Only 16 additional clusters are found in aperture 1 with 1.5 arcmin radius and only 3 in the last three apertures. The peak of the cluster signal is less constrained in the apertures 1, 3, 4, and 5 as shown in Fig. 13. The large overlap in the detection of the clusters with the different apertures is illustrated in Fig. 14 for apertures 2, 3, and 4. Compared to the statistics in the starting sample the predicted completeness has increased for the high flux sample mostly due to the fact that the cluster signal in the statistical analysis becomes better defined with increasing flux limit. Thus the statistics of aperture 2 alone gives an internal completeness estimate of 93%. Since the results of the different searches are highly correlated (see Fig. 14) we cannot easily combine the results in a statistically strict sense. A rough estimate is given by a simple extrapolation from the completeness and the sample size found for aperture 2 (93% for 433 clusters) and the additional number of 19 clusters found exclusively in other rings yielding a formal value of 97%.

The latter number should be treated with care, however, as an internal completeness check. This statistics would be more reliable if we had one homogeneous population of clusters. Since our clusters cover a wide range of richnesses and redshifts we cannot assume that all subsamples contribute to the cluster signal in Fig. 12 in the same way. If for example no significant galaxy overdensity could be detected for the high redshift clusters, this subsample would not enter into the statistics at all. Likewise, galaxy clusters for which the X-ray detections are missed in the basic source detection process are also not included in this prediction. Therefore the good agreement between the above predictions and the final results supports our confidence in the high quality of the sample but it is not a sufficient test for completeness. We discuss further external tests in Sect. 8.

$\begin{figure} \par\includegraphics[width=8.7cm,clip]{aa10210f12.ps} % \end{figure}$

Figure 13: Results for the cluster search with four of the five different circular apertures for the flux limit of the REFLEX sample. The thin (upper) line shows the statistics for the input sample and the thick (lower) line the results for the REFLEX clusters. The probability values plotted are defined by Eq. (1)

$\begin{figure} \par\includegraphics[width=7cm,clip]{aa10210f16.ps}\end{figure}$

Figure 14: Number of cluster candidates selected by means of the aperture counts in rings 1 to 3 (3, 5, 7.5 arcmin, respectively) and number of clusters found in the REFLEX Survey (values in brackets)

$\begin{figure} \par\includegraphics[width=8cm,clip]{aa10210f17.ps}\end{figure}$

Figure 15: Distribution of the numbers of galaxies detected in rings 1-3 for the clusters in the REFLEX sample. Thin line: 1.5 arcmin aperture, thick line: 3 arcmin aperture, broken line: 5 arcmin aperture

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{aa10210f18.ps}\end{figure}$

Figure 16: Distribution of the significance values of the detections of galaxy overdensities in rings 1-3 for the clusters in the REFLEX sample

Another useful illustration concerns the question of how well defined the galaxy overdensity signal is for an individual cluster. An answer is given in Figs. 15 and 16 where we show the number of galaxies (above the background density) for the galaxy counts in aperture 1, 2, and 3 for the clusters of the REFLEX sample. For aperture 2 we find for example that the typical count result is about 20 galaxies per cluster providing a signal of about $4\sigma$ . Thus in general the overdensity signal is very well defined. There is a tail to low number counts and significances which involves only a few clusters, however. For aperture 1 we note that the number counts and significance values are substantially less. Increasing the aperture size beyond 3 arcmin increases the mean significance of the galaxy counts, as seen in the results for aperture 3. But what is more important: the tail towards low significance values is not reduced if we compare aperture 3 to aperture 2. This once again shows the effectiveness of aperture 2. One should also note the strong overlap of the results of the different apertures as illustrated in Fig. 14 which is reenforcing the significance of the selection results. In fact, about 60% of all the REFLEX clusters are flagged in the counting results for all five apertures. It is not surprising that the second aperture with a 3 arcmin radius features as best adapted for our survey, since 3 arcmin corresponds to a physical scale of about 370 h₅₀^-1 kpc at the median distance of the REFLEX clusters, $z \sim 0.08$ , (see also Table 3). This corresponds to about 1.5 core radii, a good sample radius to capture the high surface density part of the clusters.

In Figs. 17 to 19 we show the galaxy number counts and significances for aperture 2 as a function of flux and redshift. While there is no striking correlation with flux we clearly note the decrease of the number counts and significance values even for the richest clusters with redshift. In Fig. 18 we also show the expected number counts for a rich cluster (with an Abell richness of 100, which is the number of galaxies within r = 3h₅₀^-1 Mpc and a magnitude interval ranging from the third brightest galaxy to a limit 2 magnitudes deeper) as a function of redshift for three magnitude limits for the galaxy detection on the plates of $b_{\rm J} = 20$ , 21, 22 mag. Galaxies are still classified in the COSMOS data base down to 22nd magnitude but the completeness is decreasing continuously over the magnitude range from $b_{\rm J} = 20$ -22. For the calculation we assume a Schechter function for the galaxy luminosity function with a slope of -1.2 and $M^*(b_{\rm J}) = -19.5$ , a cluster shape characterized by a King model with a core radius of 0.5 h₅₀^-1 Mpc, and a K-correction of $\Delta b_{\rm J} = 3z$ (see e.g. Efstathiou et al. 1988; Dalton et al. 1997). The dashed curves in Fig. 18 give then the number of galaxy counts expected for the various magnitude limits. We note that the distribution of the data points are well described by the theoretical curves with a steep rise at low redshift which is due to an increasing part of the cluster being covered by the aperture and the decrease at high redshift when only the very brightest cluster galaxies are detected. We also not the increasing difficulty to recognize clusters above a redshift of z = 0.3.

Tests based on the comparison of the cluster redshift distribution with simulations involving the REFLEX X-ray luminosity and selection function (in right ascension, declination and redshift) and assuming no evolution of the cluster population with redshift show that there is no significant deficit of clusters in the sample out to a redshift z = 0.3 (e.g. Fig. 8 in Schuecker et al. 2000). Even beyond a redshift of 0.3 where the detection of clusters in the COSMOS data becomes more difficult, we note no deficit in the cluster population. Calculations based on a no-evolution assumption, in the X-ray luminosity function as derived in the forthcoming paper (Böhringer et al. 2001a), and on the selection function derived here, lead to the prediction of an expectation value for the detection at redshifts beyond z = 0.3 of 12 clusters, where 11 have been found. This indicates that the most distant clusters in REFLEX are optically rich enough to just be captured by the galaxy count technique applied to the COSMOS data. Even the most distant clusters in the sample, which have independently been found as extended RASS sources, are detected and selected by the correlation based on the COSMOS data. The actual significance value of $1.2\sigma$ for the extreme case of the most distant REFLEX cluster at z=0.45, RXCJ1347.4-1144, ( $2.5\sigma$ for aperture 3) and $0.45\sigma$ for the second most distant cluster at z=0.42(found in aperture 1 with a $1.4\sigma$ signal) are quite low for aperture 2, however. Still, the significance in the optimal aperture is surprisingly good for the high redshifts of these clusters.

In summary, we conclude that our combined use of X-ray and optical data leads to a very successful selection of cluster candidates without an introduction of a significant optical bias, and we expect to be over 90% complete for the chosen X-ray flux limit.

$\begin{figure} \par\includegraphics[width=8cm,clip]{aa10210f19.ps}\end{figure}$

Figure 17: Distribution of the number of galaxies counted in aperture 2 versus X-ray flux. The background galaxy density has been subtracted from the aperture counts

$\begin{figure} \par\includegraphics[width=8cm,clip]{aa10210f20.ps}\end{figure}$

Figure 18: Distribution of the number of galaxies counted in aperture 2 versus redshift. Also shown are the expected number counts for this aperture for a cluster with an Abell richness of 100 for the optical magnitude limits of $b_{\rm J}$ = 20, 21, and 22, respectively. For the cluster model used to calculate these expected numbers see the description in the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{aa10210f21.ps}\end{figure}$

Figure 19: Distribution of the significance of the galaxy overdensity for the galaxies found in aperture 2 versus redshift. Note that the significance can get negative if the number of galaxies counted in the aperture is less than the background value

6 Inspection of the first selected candidate sample

6.1 Comparison of the cluster search statistics with the final results of the REFLEX Survey