A&A 369, 589-593 (2001)
DOI: 10.1051/0004-6361:20010053
Cassiopeia A dust composition and heating![[*]](/icons/foot_motif.gif)
T. Douvion1,2 - P. O. Lagage1 - E. Pantin1
1 - DSM/DAPNIA/Service d'Astrophysique,
CEA/Saclay, 91191 Gif-sur-Yvette, France
2 -
Supélec, Service des Mesures,
91192 Gif-sur-Yvette, France
Received 28 July 2000 / Accepted 9 January 2001
Abstract
Material ejected by a supernova is directly observed in the form of Fast
Moving Knots (FMK's) in the Cassiopeia A
supernova remnant. Part of this material has condensed into dust. In this
paper, by fitting the ISO mid-infrared emission of the dust, we derive the
dust composition and discuss the dust heating. The dust is found to be made
mainly of three components: pyroxene, quartz and aluminium oxide. These
components have to be heated at two different temperatures, a "hot''
temperature around 350K and a cold temperature around 90K. The physical
conditions in the knot-shocked region are such that the dust can be collisionally
heated to a temperature of 350K.
The cold dust temperature can also be well
accounted for by the knot model discussed in the paper.
The dust formation efficiency is tentatively estimated to be
of the order of 10% in this supernova.
Key words: supernova remnant - supernovae individual: Cas A
dust - infrared: general
Cassiopeia A (Cas A) is the youngest SuperNova Remnant (SNR) known in our
galaxy. The date of the SN explosion which has given birth to the SNR is
estimated to be 1680 (Fesen et al. 1988).
The SN was subluminous and/or heavely obscured, since it was not noticed,
except perhaps by Flamsteed (Ashworth 1980). The progenitor of the SN was a
massive star (Vink et al. 1996; Jansen et al. 1988;
Fabian et al. 1980), probably of Wolf-Rayet type (Fesen et al. 1988). Freshly
synthesized SN material is observed in the form of Fast Moving Knots (FMK's)
(Baade & Minkowsky 1954; Chevalier & Kirshner 1979; van den Bergh &
Kamper 1985 and earlier papers).
There are several evidences indicating that part of the SN ejecta has
condensed into dust (Lagage et al. 1996; Arendt et al. 1999,
hereafter ADM99, Douvion et al. 1999, hereafter DLC99).
In this paper, after having presented in Sect. 2 the
observational material obtained with the Infrared Space Observatory (ISO)
(Kessler et al. 1996),
we discuss, in Sect. 3, the dust composition and, in Sect. 4, the dust heating.
The mid-InfraRed (IR) wavelength range is rich with dust features, especially
silicate features. The Short Wavelength Spectrometer (SWS) on board of ISO
(de Graauw et al. 1996) has been a powerful instrument to reveal and study
dust features (e.g. Waelkens et al. 1999).
The SWS observation of Cas A, discussed here, was performed on December
5th 1997. The observation consists of a low-resolution full grating
scan from 2.38 to 45.2 m. The position on the sky of the SWS slit
is shown in Fig. 1.
m. The position on the sky of the SWS slit
is shown in Fig. 1.
![\begin{figure}
\includegraphics[width=10.8cm]{h2563f1.eps}\end{figure}](/articles/aa/full/2001/14/aah2563/Timg3.gif) |
Figure 1:
Optical image of the
northern part of the Cas A SNR in the [OIII] lines at
4959 and 5007 Å, obtained with the SIS instrument mounted on the Canada
France Hawaii Telescope (CFHT) on August 25th
1998. The white rectangle indicates the size and the position of
the ISO-SWS slit aperture of the observations discussed in this paper |
| Open with DEXTER |
The data reduction was first performed using the Observer SWS Interactive
Analysis (OSIA![[*]](/icons/foot_motif.gif) ) package.
Given that the Cas A flux is close to SWS sensitivity limit, additional data
reduction was needed. Indeed, the data scans are corrupted with random
"jumps'' in the signal, originating probably from high energy particles
hitting the detectors; these "jumps'' may create long term shifts in the
signal and degrade seriously the quality of the dark. To deal with
the jump problem, we have used a package developed under SIA1(Spectroscopic Interactive Analysis) by Pantin et al. (1999).
Even with this careful data reduction, the signal to noise ratio is high
enough only in the 16-29
) package.
Given that the Cas A flux is close to SWS sensitivity limit, additional data
reduction was needed. Indeed, the data scans are corrupted with random
"jumps'' in the signal, originating probably from high energy particles
hitting the detectors; these "jumps'' may create long term shifts in the
signal and degrade seriously the quality of the dark. To deal with
the jump problem, we have used a package developed under SIA1(Spectroscopic Interactive Analysis) by Pantin et al. (1999).
Even with this careful data reduction, the signal to noise ratio is high
enough only in the 16-29  m wavelength range. In this wavelength range,
the aperture of the SWS slit is equal to 14
m wavelength range. In this wavelength range,
the aperture of the SWS slit is equal to 14
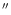 by 27
by 27
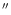 .
The resulting spectrum
is displayed in Fig. 2. The spectrum is similar in shape and flux level to
the spectrum N3 discussed in ADM99. The slit positions on the sky
corresponding to the two spectra were very close, so that, given the
pointing uncertainties of ISO, the main emitting area is probably
contained in both slit apertures.
.
The resulting spectrum
is displayed in Fig. 2. The spectrum is similar in shape and flux level to
the spectrum N3 discussed in ADM99. The slit positions on the sky
corresponding to the two spectra were very close, so that, given the
pointing uncertainties of ISO, the main emitting area is probably
contained in both slit apertures.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2563F2.PS}\end{figure}](/articles/aa/full/2001/14/aah2563/Timg5.gif) |
Figure 2:
Full line: ISOCAM (6-16  m) and ISO-SWS
(16-29 m) and ISO-SWS
(16-29 m) fluxes obtained in the aperture plotted in Fig. 1, as
a function of the wavelength. The uncertainties are of m) fluxes obtained in the aperture plotted in Fig. 1, as
a function of the wavelength. The uncertainties are of 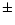 6mJy on
CAM data and 6mJy on
CAM data and 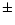 1Jy on SWS data. In addition to the continuum emission
that is discussed in the paper, we identify forbidden ionic line emission
from [ArII] (7.0 1Jy on SWS data. In addition to the continuum emission
that is discussed in the paper, we identify forbidden ionic line emission
from [ArII] (7.0 m), [ArIII] (9.0 m), [ArIII] (9.0 m), [SIV] (10.5 m), [SIV] (10.5 m),
[NeII] (12.8 m),
[NeII] (12.8 m), [NeV] (14.3 m), [NeV] (14.3 m, very weak), [NeIII] (15.5 m, very weak), [NeIII] (15.5 m)
and [OIII] (25.9 m)
and [OIII] (25.9 m). The dashed line is the fit of the continuum
emission with Mg-protosilicates heated at 169K, as proposed by ADM99 m). The dashed line is the fit of the continuum
emission with Mg-protosilicates heated at 169K, as proposed by ADM99 |
| Open with DEXTER |
The spectrum at wavelengths shorter than 16 m was obtained with ISOCAM,
the camera on board of ISO (Cesarsky et al. 1996).
The ISOCAM observations were performed on December 5th 1996, with a
pixel field of view of 6
m was obtained with ISOCAM,
the camera on board of ISO (Cesarsky et al. 1996).
The ISOCAM observations were performed on December 5th 1996, with a
pixel field of view of 6
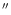 and a corresponding total field of view of
and a corresponding total field of view of
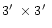 .
The field was centered on the northern part of the remnant. For each pixel,
we have a spectrum from 6 to 16.5
.
The field was centered on the northern part of the remnant. For each pixel,
we have a spectrum from 6 to 16.5  m, obtained by
rotating the Circular Variable Filter (CVF) of ISOCAM; the spectral resolution
obtained that way is
m, obtained by
rotating the Circular Variable Filter (CVF) of ISOCAM; the spectral resolution
obtained that way is
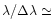 40. The data reduction was
performed with the Cam Interactive Analysis
40. The data reduction was
performed with the Cam Interactive Analysis![[*]](/icons/foot_motif.gif) (CIA) package. We have reconstructed the 7 to 16
(CIA) package. We have reconstructed the 7 to 16 m fluxes in the
14
m fluxes in the
14
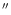 by 27
by 27
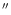 SWS aperture, by co-adding the ISOCAM fluxes in this area.
The resulting spectrum is shown in Fig. 2. Note that no re-scaling was
applied to connect the SWS spectrum and the ISOCAM spectrum.
SWS aperture, by co-adding the ISOCAM fluxes in this area.
The resulting spectrum is shown in Fig. 2. Note that no re-scaling was
applied to connect the SWS spectrum and the ISOCAM spectrum.
Following ADM99, we have first tried to fit the spectrum of Fig. 2 with
Mg-protosilicates at a temperature of 169K; the optical constants of
Mg-protosilicates have been taken from Dorschner et al. (1980). The
16-29 m part of the spectrum is well fitted, but the model predicts
a 10
m part of the spectrum is well fitted, but the model predicts
a 10 m feature quite different from the observed one (see Fig. 2).
Another material has to be found. The choice of materials is large, so
that we have used, as a starting point, the materials which
are predicted to form in abundance from SN material, i.e. MgSiO3(pyroxene) and Al2O3 (Kozasa et al. 1991;
Kozasa & Hisato 1997).
m feature quite different from the observed one (see Fig. 2).
Another material has to be found. The choice of materials is large, so
that we have used, as a starting point, the materials which
are predicted to form in abundance from SN material, i.e. MgSiO3(pyroxene) and Al2O3 (Kozasa et al. 1991;
Kozasa & Hisato 1997).
We first focused on fitting the feature at 9.5 m. The use of
MgSiO3 leads to a better fit of the feature than Mg-protosilicates;
however, the predicted flux is too low in the 7.5-8.5
m. The use of
MgSiO3 leads to a better fit of the feature than Mg-protosilicates;
however, the predicted flux is too low in the 7.5-8.5 m range
(see Fig. 3). Whatever the various silicates we use, (olivine or pyroxene with
various Mg/Fe ratio, Dorschner et al. 1995,
various protosilicates, Dorschner et al. 1980, Draine and Lee
astronomical silicates, Draine
& Lee 1984), whatever the dust temperature is, the problem persists.
The use of Al2O3 is of no help in that region. To solve the
problem, we had to introduce another dust component made of quartz
(SiO2). As can be seen in Fig. 3, a good fit of the 9.5
m range
(see Fig. 3). Whatever the various silicates we use, (olivine or pyroxene with
various Mg/Fe ratio, Dorschner et al. 1995,
various protosilicates, Dorschner et al. 1980, Draine and Lee
astronomical silicates, Draine
& Lee 1984), whatever the dust temperature is, the problem persists.
The use of Al2O3 is of no help in that region. To solve the
problem, we had to introduce another dust component made of quartz
(SiO2). As can be seen in Fig. 3, a good fit of the 9.5 m feature
is obtained with a contribution of both pyroxene and quartz at a
relatively high temperature (345K for pyroxene and 361K for quartz);
(the optical constants of the materials are obtained from Dorschner et al.
1980 and from the database on the web site of the Jena institute,
http://www.astro.uni-jena.de/Group/Subgroups/ Labor/Labor/databases.html).
It is not surprising to find quartz here. Indeed, quartz can be produced
with a good efficiency from SN material (Kozasa 2000, private communication).
In the absence of magnesium, the formation of pyroxene through the reaction
m feature
is obtained with a contribution of both pyroxene and quartz at a
relatively high temperature (345K for pyroxene and 361K for quartz);
(the optical constants of the materials are obtained from Dorschner et al.
1980 and from the database on the web site of the Jena institute,
http://www.astro.uni-jena.de/Group/Subgroups/ Labor/Labor/databases.html).
It is not surprising to find quartz here. Indeed, quartz can be produced
with a good efficiency from SN material (Kozasa 2000, private communication).
In the absence of magnesium, the formation of pyroxene through the reaction
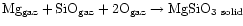 is quenched
and quartz is formed instead. If the element mixing is uncomplete, as
claimed in DLC99, then there is indeed a layer
inside the SN, with Si, O and lack of Mg (Woosley & Weaver 1995). In case
of complete mixing, given that Si is more abundant that Mg, the formation of
SiO2 is also possible.
is quenched
and quartz is formed instead. If the element mixing is uncomplete, as
claimed in DLC99, then there is indeed a layer
inside the SN, with Si, O and lack of Mg (Woosley & Weaver 1995). In case
of complete mixing, given that Si is more abundant that Mg, the formation of
SiO2 is also possible.
![\begin{figure}
\includegraphics[width=6cm,clip]{h2563f3.eps}\end{figure}](/articles/aa/full/2001/14/aah2563/Timg9.gif) |
Figure 3:
ISOCAM and ISO-SWS data fitted with pyroxene (full blue and
green lines), quartz (dashed blue and green lines) and aluminium oxides
(dot-dashed blue and green lines). The hot component is figured in green,
and the cold component in blue. The red dashed line is the possible
synchrotron continuum contribution (slope from Baars et al. 1977). The red line
is the result of the sum of the contributions of the various components |
| Open with DEXTER |
The same relative quantities of quartz and pyroxene, but at a cooler
temperature (83K for pyroxene and 93K for quartz), lead also to
a good fit of the data in the 16-29 m wavelength range. Finally,
the presence of aluminium oxides (hot at 351K and cold at 113K) accounts
for the 12-13
m wavelength range. Finally,
the presence of aluminium oxides (hot at 351K and cold at 113K) accounts
for the 12-13 m feature, and contributes dominantly to the continuum
from 13 to 16
m feature, and contributes dominantly to the continuum
from 13 to 16 m. Al2O3 exists in different forms; the best
fit was obtained with a mixture of Al2O3 called ISAS
in the paper by Koike et al. (1995); the mixture mainly consists of
m. Al2O3 exists in different forms; the best
fit was obtained with a mixture of Al2O3 called ISAS
in the paper by Koike et al. (1995); the mixture mainly consists of
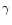 -Al2O3. Note that we had to decrease by a factor of 5
the relative abundance of Al2O3 compared to MgSiO3,
when going from the hot component to the cold component (see next section).
The resulting fit is shown in Fig. 3.
-Al2O3. Note that we had to decrease by a factor of 5
the relative abundance of Al2O3 compared to MgSiO3,
when going from the hot component to the cold component (see next section).
The resulting fit is shown in Fig. 3.
In the previous section, we only discussed the dust composition; in this
section, we discuss the physical model we have used to
account for the dust heating. As pointed out in the paper by Lagage et al.
(1996), the dust is probably SN condensates embedded in the FMK's. As
discussed by Dwek & Werner (1981), the dominant dust heating mechanism in
the FMK's is collisions between the dust and the electrons of the plasma
inside the knots. To calculate the heating of the dust, we need to know the
physical conditions inside the FMK's. Constraints on these physical
conditions can in principle be obtained from optical observations.
There is not yet a model reproducing all the optical observations of a knot. The most developed model is, so far, the model by Sutherland & Dopita (1995) (SD95 hereafter). The basis of the model is the encounter of a FMK with the reverse shock of the SN, which induces the propagation of a shock wave into the knot, preceeded by the propagation of an ionisation front.
Oxygen lines arise both at the ionisation front and at the shock, which becomes rapidly radiative. In the following, we adopt the SD95 model
with a shock velocity inside the knot of
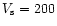 kms-1. We have chosen this model because it is the one which predicts the right [OIII] 4363 /[OIII] 4959+5007 line flux ratio.
Most of the optical [OIII] lines are produced at the ionisation front,
which propagates at a high speed of 3300kms-1.
The flux observed in the
kms-1. We have chosen this model because it is the one which predicts the right [OIII] 4363 /[OIII] 4959+5007 line flux ratio.
Most of the optical [OIII] lines are produced at the ionisation front,
which propagates at a high speed of 3300kms-1.
The flux observed in the
![$\rm [OIII]~4959$](/articles/aa/full/2001/14/aah2563/img12.gif) +5007Å lines allows us to
determine the density in this region using the SD95 model. For the
bright optical knot contained in the SWS aperture (see Fig. 1), we
measure
+5007Å lines allows us to
determine the density in this region using the SD95 model. For the
bright optical knot contained in the SWS aperture (see Fig. 1), we
measure
![$F_{\rm Single Knot}([{\rm OIII}])=1.5$](/articles/aa/full/2001/14/aah2563/img13.gif) 10-11ergcm-2s-1from CFHT observations, taking into account the extinction in the
same way as Dinerstein et al. (1987).
The electronical temperature, derived from SD95 for the part of the
ionisation front where [OIII] is present, is 7103K and, given
the physical parameters of the lines emission deduced from Osterbrock
(1989), we obtain a knot electronic density,
10-11ergcm-2s-1from CFHT observations, taking into account the extinction in the
same way as Dinerstein et al. (1987).
The electronical temperature, derived from SD95 for the part of the
ionisation front where [OIII] is present, is 7103K and, given
the physical parameters of the lines emission deduced from Osterbrock
(1989), we obtain a knot electronic density, 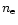 ,
of 2.4103cm-3.
We assume a spherical geometry and we take Cas A at a distance of 3.4kpc
(Reed et al. 1995), and a typical diameter knot size of 1
,
of 2.4103cm-3.
We assume a spherical geometry and we take Cas A at a distance of 3.4kpc
(Reed et al. 1995), and a typical diameter knot size of 1
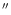 ,
(size of
the brightest optical knot in the SWS aperture, as deduced after
deconvolution of the optical image shown in Fig. 1).
,
(size of
the brightest optical knot in the SWS aperture, as deduced after
deconvolution of the optical image shown in Fig. 1).
We consider here the dust heating in the shock cooling region.
The electronic
temperature of the shocked material decreases rapidly in the
cooling region from
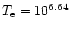 K to
K to
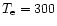 K; the
associated electronic density varies from
K; the
associated electronic density varies from
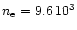 cm-3 to
cm-3 to
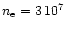 cm-3; (rescaled from SD95).
The physical conditions in this region are such that the dust can be
collisionally heated at a temperature corresponding to the temperature of
the "hot'' dust component discussed in the previous section. Thus we have
considered that the hot dust component was associated with this
cooling region. In order to derive the "hot'' dust mass from the IR
observations, we need to know the size of the dust.
We have no observational constraint on these sizes, so that we have taken
the sizes calculated by Kozasa et al. (1997) for newly formed SN dust:
70Å for the MgSiO3, and 10Å for the Al2O3 grains; we
have also used 70Å for the SiO2 grains. With these sizes and given the
dust heating, the IR luminosities imply 7.810-9
cm-3; (rescaled from SD95).
The physical conditions in this region are such that the dust can be
collisionally heated at a temperature corresponding to the temperature of
the "hot'' dust component discussed in the previous section. Thus we have
considered that the hot dust component was associated with this
cooling region. In order to derive the "hot'' dust mass from the IR
observations, we need to know the size of the dust.
We have no observational constraint on these sizes, so that we have taken
the sizes calculated by Kozasa et al. (1997) for newly formed SN dust:
70Å for the MgSiO3, and 10Å for the Al2O3 grains; we
have also used 70Å for the SiO2 grains. With these sizes and given the
dust heating, the IR luminosities imply 7.810-9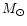 of MgSiO3, 3.110-9
of MgSiO3, 3.110-9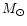 of SiO2 and
1.110-9
of SiO2 and
1.110-9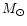 of Al2O3.
Note that
a 30Å change in the size of a 70Å grain leads to
a change by
a factor 3 of the masses.
of Al2O3.
Note that
a 30Å change in the size of a 70Å grain leads to
a change by
a factor 3 of the masses.
Are such masses compatible with dust made from SN material?
In DLC99, we have argued that the dust observed from Cas A was silicate dust
made from SN material; the layer in the SN where silicate components
(Si, Mg and O) are present, was identified in Fig. 2 of DLC99.
If we take the relative abundance of elements in the "silicate layer''
(Woosley & Weaver 1995), we can evaluate the mass ratio of the different
dust species relatively to the gas. Assuming that the dust formation
efficiency is 100%, then almost all the magnesium and part
of the silicon is locked in MgSiO3 dust grains; the remaining silicon
is locked in SiO2 dust grains; all the aluminium is locked in
Al2O3 dust grains, and the remaining gas is almost entirely
made of oxygen. In these conditions,
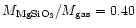 ,
,
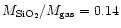 and
and
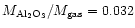 .
The size of the cooling region, and the density derived from CFHT observations
allow to calculate the mass of gas available in the cooling area.
This region is very thin; SD95 obtained a cooling length,
.
The size of the cooling region, and the density derived from CFHT observations
allow to calculate the mass of gas available in the cooling area.
This region is very thin; SD95 obtained a cooling length,
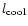 ,
of 21011cm for an initial oxygen density of
1.2103cm-3 (here the oxygen density has been taken
equal to
,
of 21011cm for an initial oxygen density of
1.2103cm-3 (here the oxygen density has been taken
equal to 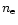 /2 according to the degree of oxygen ionization
calculated in SD95 in the ionization area). Then the mass of gas available in the
cooling region of a
single knot is 1.310-7
/2 according to the degree of oxygen ionization
calculated in SD95 in the ionization area). Then the mass of gas available in the
cooling region of a
single knot is 1.310-7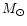 ;
consequently, if we consider a dust formation efficiency of 100%, we obtain
;
consequently, if we consider a dust formation efficiency of 100%, we obtain
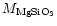 = 5.310-8
= 5.310-8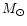 ,
,
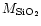 = 1.810-8
= 1.810-8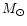 and
and
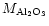 = 4.310-9
= 4.310-9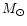 .
Thus the observed and potentially available dust masses are compatible.
.
Thus the observed and potentially available dust masses are compatible.
Comparing the observed dust masses and the calculated maximum dust mass produced from SN material in a knot, we can evaluate the dust "formation'' efficiency. When the SWS aperture contains many knots, a map obtained at 9.77 m with ISOCAM using the smallest pixel field of view
of 1.5
m with ISOCAM using the smallest pixel field of view
of 1.5
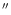 ,
shows that the hot component originates mainly (50%) from the bright knot of the SWS aperture of
Fig. 1. For this knot, we can derive an estimate of dust formation efficiency of
,
shows that the hot component originates mainly (50%) from the bright knot of the SWS aperture of
Fig. 1. For this knot, we can derive an estimate of dust formation efficiency of
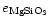 = 7.4%,
= 7.4%,
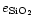 = 8.6% and
= 8.6% and
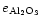 = 13%.
Given the simplifications in the model and the
uncertainties in the parameters of the region (a factor 2 of error on the initial
density leads to a factor 2 of error on the efficiency), we can just state that the
efficiency is of the order of 10%. Note that the observed
= 13%.
Given the simplifications in the model and the
uncertainties in the parameters of the region (a factor 2 of error on the initial
density leads to a factor 2 of error on the efficiency), we can just state that the
efficiency is of the order of 10%. Note that the observed
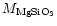 /
/
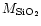 and
and
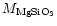 /
/
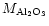 ratios are well predicted by the model.
ratios are well predicted by the model.
Much more dust is present in the region behind the
cooling region. From the SD95 model, we can deduce that the "mean'' physical
conditions in that region are
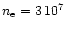 cm-3 and
cm-3 and
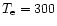 K. Given these physical conditions and assuming the same
dust sizes as for the "hot'' component, we can compute the dust temperature
and deduce from the observed fluxes the "cold'' dust masses needed:
K. Given these physical conditions and assuming the same
dust sizes as for the "hot'' component, we can compute the dust temperature
and deduce from the observed fluxes the "cold'' dust masses needed:
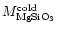 = 1.110-4
= 1.110-4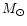 ,
,
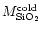 = 4.410-5
= 4.410-5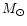 and
and
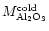 = 3.210-6
= 3.210-6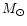 .
.
The dust mass in the region behind the cooling area
is difficult to determine. An upper limit to the dust mass can be obtained by
considering the total dust mass in a knot. From the gas to dust mass ratio (DLC99)
and the density previously discussed,
we can derive a total dust mass of
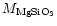 = 4.210-4
= 4.210-4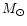 ,
,
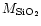 = 1.510-4
= 1.510-4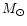 and
and
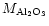 = 3.410-5
= 3.410-5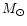 ,
in the brightest knot in the SWS aperture.
If we assume, as for the hot component, that half of the cold dust is located into this knot, the observed cold component from the knot represents about 14% of the maximum MgSiO3 and SiO2 dust masses. We are in the uncomfortable situation that the efficiency deduced for the cold dust is somewhat higher than that deduced from the hot component. The assumption that half of the observed cold dust is present in a bright knot, which cannot be tested because of the poor angular resolution of the SWS instrument, is questionable. Indeed the cold component emission lasts longer than the hot component emission, just because of the rapid cooling of region where the dust hot component is emitted and the rapid propagation of the shock inside the knot. Then it is quite possible that several knots with no or little hot dust emission are present in the SWS beam; this would explain why we
observe so much dust in the cold component.
Note that the Al2O3 cold component mass is only 5% of the total expected
dust mass. The origin of such a large depletion compared to MgSiO3 or
SiO2 may be linked to the small size (10 Å) of the grains, which are
more easily destroyed by sputtering effects in the cooling area than
the 70 Å sized particles.
,
in the brightest knot in the SWS aperture.
If we assume, as for the hot component, that half of the cold dust is located into this knot, the observed cold component from the knot represents about 14% of the maximum MgSiO3 and SiO2 dust masses. We are in the uncomfortable situation that the efficiency deduced for the cold dust is somewhat higher than that deduced from the hot component. The assumption that half of the observed cold dust is present in a bright knot, which cannot be tested because of the poor angular resolution of the SWS instrument, is questionable. Indeed the cold component emission lasts longer than the hot component emission, just because of the rapid cooling of region where the dust hot component is emitted and the rapid propagation of the shock inside the knot. Then it is quite possible that several knots with no or little hot dust emission are present in the SWS beam; this would explain why we
observe so much dust in the cold component.
Note that the Al2O3 cold component mass is only 5% of the total expected
dust mass. The origin of such a large depletion compared to MgSiO3 or
SiO2 may be linked to the small size (10 Å) of the grains, which are
more easily destroyed by sputtering effects in the cooling area than
the 70 Å sized particles.
One consequence of the model presented here is the temporal correlation
between the optical emission at the shock and the hot dust emission. We also predict an
increase with time of the IR emission from the cold dust component.
Monitoring the knots both in the IR and the optical on the time scale of the
knot optical lifetime (about 30 years) should help qualifying the model
presented here. High angular resolution at 20 m are also needed to assess if there are indeed knots emitting mostly at 20
m are also needed to assess if there are indeed knots emitting mostly at 20 m, with faint counterparts in the optical or at 10
m, with faint counterparts in the optical or at 10 m.
m.
Acknowledgements
We thanks A. Jones and J.-P. Chièze for enlightening discussions on shocks and
their effects, and D. Péquignot for discussions on the optical emission.
-
Arendt, R. G., Dwek, E., &
Moseley, S. H. 1999, ApJ, 521, 234
(ADM99)
In the text
NASA ADS
- Ashworth, W. B. 1980, J.
Hist. Astron., 11, 1
In the text
NASA ADS
- Baade, W., & Minkowski, R. 1954,
ApJ, 501, 206
In the text
- Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., &
Witzel, A. 1977, A
 A, 61, 99
In the text
NASA ADS
A, 61, 99
In the text
NASA ADS
- Cesarsky, C. J., Abergel, A.,
Agnese, P., et al. 1996, A
 A, 315, L32
In the text
NASA ADS
A, 315, L32
In the text
NASA ADS
- Chevalier, R. A., &
Kirshner, R. P. 1979, ApJ, 233, 154
In the text
NASA ADS
- de Graauw, T., Haser, L. N.,
Beintema, D. A., et al. 1996, A
 A, 315, L49
In the text
NASA ADS
A, 315, L49
In the text
NASA ADS
- Dinerstein, H. L., Lester, D. F.,
Rank, D. M., et al. 1987, ApJ, 312, 314
In the text
NASA ADS
-
Dorschner, J., Friedmann, C., Gütler, J., & Duley, W. W. 1980, A
 ASS, 68, 159
In the text
ASS, 68, 159
In the text
-
Dorschner, J., Begemann, B., Henning, T., Jäger, C., & Mutschke, H. 1995,
A
 A, 300, 503
In the text
NASA ADS
A, 300, 503
In the text
NASA ADS
- Douvion, T., Lagage,
P.-O., & Cesarsky, C. J. 1999, A
 A, 352, L111
(DLC99)
In the text
NASA ADS
A, 352, L111
(DLC99)
In the text
NASA ADS
- Draine, B. T., & Lee, H. M. 1984,
ApJ, 2885, 89
In the text
- Dwek, E., & Werner, M. W. 1981,
ApJ, 248, 138
In the text
NASA ADS
- Fabian, A. C., Willingale, R.,
Pye, J. P, Murray, S. S., & Fabbiano, G. 1980, MNRAS, 193, 175
In the text
NASA ADS
- Fesen, R. A., Becker,
R. H., & Goodrich, R. W. 1988, ApJ, 329, L89
In the text
NASA ADS
- Jansen, F. A., Smith, A., Bleeker,
J. A. M., et al. 1988, ApJ, 331, 949
In the text
NASA ADS
- Kessler, M. F., Steinz, J. A.,
Anderegg, M. E., et al. 1996, A
 A, 315, L27
In the text
NASA ADS
A, 315, L27
In the text
NASA ADS
- Koike, C., Kaito, C., Yamamoto, T.,
et al. 1995, Icarus, 114, 203
In the text
NASA ADS
- Kozasa, T., Hasegawa,
H., & Nomoto, K. 1991, A
 A, 249, 474
In the text
NASA ADS
A, 249, 474
In the text
NASA ADS
- Kozasa, T., & Hisato, S. 1997,
APSS, 255, Issue 1/2, 437
In the text
- Lagage, P. O, Claret, A., Ballet, J.,
et al. 1996, A
 A, 315, L273
In the text
NASA ADS
A, 315, L273
In the text
NASA ADS
- Osterbrock, D. E. 1989, Astrophysics of
gaseous nebulae and active galactic nuclei (University Science Books)
In the text
- Pantin, E., Waelkens, C., &
Malfait, K. 1999, The Universe as seen by ISO, ESA SP-427, 385
In the text
- Reed, J. E., Hester, J. J., Fabian, A. C., &
Winkler, P. F. 1995, ApJ, 440, 706
In the text
NASA ADS
- Sutherland, R. S., &
Dopita, M. A. 1995, ApJ, 439, 381
(SD95)
In the text
NASA ADS
- van den Bergh, S., & Kamper,
K. 1985, ApJ, 293, 537
In the text
NASA ADS
- Vink, J., Kaastra, J. S., &
Bleeker, J. A. M. 1996, A
 A, 307, L41
In the text
NASA ADS
A, 307, L41
In the text
NASA ADS
- Waelkens, C., Malfait, K.,
Waters, L. B. F. M., & de Graauw, Th. 1999,
The Universe as seen by ISO, ESA SP-427, 607
In the text
- Woosley, S. E., & Weaver, T. A.
1995, ApJS, 101, 181
In the text
NASA ADS
Copyright ESO 2001
![\begin{figure}
\includegraphics[width=10.8cm]{h2563f1.eps}\end{figure}](/articles/aa/full/2001/14/aah2563/Timg3.gif)
![]() m. The use of
MgSiO3 leads to a better fit of the feature than Mg-protosilicates;
however, the predicted flux is too low in the 7.5-8.5
m. The use of
MgSiO3 leads to a better fit of the feature than Mg-protosilicates;
however, the predicted flux is too low in the 7.5-8.5![]() m range
(see Fig. 3). Whatever the various silicates we use, (olivine or pyroxene with
various Mg/Fe ratio, Dorschner et al. 1995,
various protosilicates, Dorschner et al. 1980, Draine and Lee
astronomical silicates, Draine
& Lee 1984), whatever the dust temperature is, the problem persists.
The use of Al2O3 is of no help in that region. To solve the
problem, we had to introduce another dust component made of quartz
(SiO2). As can be seen in Fig. 3, a good fit of the 9.5
m range
(see Fig. 3). Whatever the various silicates we use, (olivine or pyroxene with
various Mg/Fe ratio, Dorschner et al. 1995,
various protosilicates, Dorschner et al. 1980, Draine and Lee
astronomical silicates, Draine
& Lee 1984), whatever the dust temperature is, the problem persists.
The use of Al2O3 is of no help in that region. To solve the
problem, we had to introduce another dust component made of quartz
(SiO2). As can be seen in Fig. 3, a good fit of the 9.5![]() m feature
is obtained with a contribution of both pyroxene and quartz at a
relatively high temperature (345K for pyroxene and 361K for quartz);
(the optical constants of the materials are obtained from Dorschner et al.
1980 and from the database on the web site of the Jena institute,
http://www.astro.uni-jena.de/Group/Subgroups/ Labor/Labor/databases.html).
It is not surprising to find quartz here. Indeed, quartz can be produced
with a good efficiency from SN material (Kozasa 2000, private communication).
In the absence of magnesium, the formation of pyroxene through the reaction
m feature
is obtained with a contribution of both pyroxene and quartz at a
relatively high temperature (345K for pyroxene and 361K for quartz);
(the optical constants of the materials are obtained from Dorschner et al.
1980 and from the database on the web site of the Jena institute,
http://www.astro.uni-jena.de/Group/Subgroups/ Labor/Labor/databases.html).
It is not surprising to find quartz here. Indeed, quartz can be produced
with a good efficiency from SN material (Kozasa 2000, private communication).
In the absence of magnesium, the formation of pyroxene through the reaction
![]() is quenched
and quartz is formed instead. If the element mixing is uncomplete, as
claimed in DLC99, then there is indeed a layer
inside the SN, with Si, O and lack of Mg (Woosley & Weaver 1995). In case
of complete mixing, given that Si is more abundant that Mg, the formation of
SiO2 is also possible.
is quenched
and quartz is formed instead. If the element mixing is uncomplete, as
claimed in DLC99, then there is indeed a layer
inside the SN, with Si, O and lack of Mg (Woosley & Weaver 1995). In case
of complete mixing, given that Si is more abundant that Mg, the formation of
SiO2 is also possible.
![]() m wavelength range. Finally,
the presence of aluminium oxides (hot at 351K and cold at 113K) accounts
for the 12-13
m wavelength range. Finally,
the presence of aluminium oxides (hot at 351K and cold at 113K) accounts
for the 12-13![]() m feature, and contributes dominantly to the continuum
from 13 to 16
m feature, and contributes dominantly to the continuum
from 13 to 16![]() m. Al2O3 exists in different forms; the best
fit was obtained with a mixture of Al2O3 called ISAS
in the paper by Koike et al. (1995); the mixture mainly consists of
m. Al2O3 exists in different forms; the best
fit was obtained with a mixture of Al2O3 called ISAS
in the paper by Koike et al. (1995); the mixture mainly consists of
![]() -Al2O3. Note that we had to decrease by a factor of 5
the relative abundance of Al2O3 compared to MgSiO3,
when going from the hot component to the cold component (see next section).
The resulting fit is shown in Fig. 3.
-Al2O3. Note that we had to decrease by a factor of 5
the relative abundance of Al2O3 compared to MgSiO3,
when going from the hot component to the cold component (see next section).
The resulting fit is shown in Fig. 3.
![]() ,
,
![]() and
and
![]() .
The size of the cooling region, and the density derived from CFHT observations
allow to calculate the mass of gas available in the cooling area.
This region is very thin; SD95 obtained a cooling length,
.
The size of the cooling region, and the density derived from CFHT observations
allow to calculate the mass of gas available in the cooling area.
This region is very thin; SD95 obtained a cooling length,
![]() ,
of 21011cm for an initial oxygen density of
1.2103cm-3 (here the oxygen density has been taken
equal to
,
of 21011cm for an initial oxygen density of
1.2103cm-3 (here the oxygen density has been taken
equal to ![]() /2 according to the degree of oxygen ionization
calculated in SD95 in the ionization area). Then the mass of gas available in the
cooling region of a
single knot is 1.310-7
/2 according to the degree of oxygen ionization
calculated in SD95 in the ionization area). Then the mass of gas available in the
cooling region of a
single knot is 1.310-7![]() ;
consequently, if we consider a dust formation efficiency of 100%, we obtain
;
consequently, if we consider a dust formation efficiency of 100%, we obtain
![]() = 5.310-8
= 5.310-8![]() ,
,
![]() = 1.810-8
= 1.810-8![]() and
and
![]() = 4.310-9
= 4.310-9![]() .
Thus the observed and potentially available dust masses are compatible.
.
Thus the observed and potentially available dust masses are compatible.
![]() m with ISOCAM using the smallest pixel field of view
of 1.5
m with ISOCAM using the smallest pixel field of view
of 1.5
![]() ,
shows that the hot component originates mainly (50%) from the bright knot of the SWS aperture of
Fig. 1. For this knot, we can derive an estimate of dust formation efficiency of
,
shows that the hot component originates mainly (50%) from the bright knot of the SWS aperture of
Fig. 1. For this knot, we can derive an estimate of dust formation efficiency of
![]() = 7.4%,
= 7.4%,
![]() = 8.6% and
= 8.6% and
![]() = 13%.
Given the simplifications in the model and the
uncertainties in the parameters of the region (a factor 2 of error on the initial
density leads to a factor 2 of error on the efficiency), we can just state that the
efficiency is of the order of 10%. Note that the observed
= 13%.
Given the simplifications in the model and the
uncertainties in the parameters of the region (a factor 2 of error on the initial
density leads to a factor 2 of error on the efficiency), we can just state that the
efficiency is of the order of 10%. Note that the observed
![]() /
/
![]() and
and
![]() /
/
![]() ratios are well predicted by the model.
ratios are well predicted by the model.
![]() = 4.210-4
= 4.210-4![]() ,
,
![]() = 1.510-4
= 1.510-4![]() and
and
![]() = 3.410-5
= 3.410-5![]() ,
in the brightest knot in the SWS aperture.
If we assume, as for the hot component, that half of the cold dust is located into this knot, the observed cold component from the knot represents about 14% of the maximum MgSiO3 and SiO2 dust masses. We are in the uncomfortable situation that the efficiency deduced for the cold dust is somewhat higher than that deduced from the hot component. The assumption that half of the observed cold dust is present in a bright knot, which cannot be tested because of the poor angular resolution of the SWS instrument, is questionable. Indeed the cold component emission lasts longer than the hot component emission, just because of the rapid cooling of region where the dust hot component is emitted and the rapid propagation of the shock inside the knot. Then it is quite possible that several knots with no or little hot dust emission are present in the SWS beam; this would explain why we
observe so much dust in the cold component.
Note that the Al2O3 cold component mass is only 5% of the total expected
dust mass. The origin of such a large depletion compared to MgSiO3 or
SiO2 may be linked to the small size (10 Å) of the grains, which are
more easily destroyed by sputtering effects in the cooling area than
the 70 Å sized particles.
,
in the brightest knot in the SWS aperture.
If we assume, as for the hot component, that half of the cold dust is located into this knot, the observed cold component from the knot represents about 14% of the maximum MgSiO3 and SiO2 dust masses. We are in the uncomfortable situation that the efficiency deduced for the cold dust is somewhat higher than that deduced from the hot component. The assumption that half of the observed cold dust is present in a bright knot, which cannot be tested because of the poor angular resolution of the SWS instrument, is questionable. Indeed the cold component emission lasts longer than the hot component emission, just because of the rapid cooling of region where the dust hot component is emitted and the rapid propagation of the shock inside the knot. Then it is quite possible that several knots with no or little hot dust emission are present in the SWS beam; this would explain why we
observe so much dust in the cold component.
Note that the Al2O3 cold component mass is only 5% of the total expected
dust mass. The origin of such a large depletion compared to MgSiO3 or
SiO2 may be linked to the small size (10 Å) of the grains, which are
more easily destroyed by sputtering effects in the cooling area than
the 70 Å sized particles.
![]() m are also needed to assess if there are indeed knots emitting mostly at 20
m are also needed to assess if there are indeed knots emitting mostly at 20![]() m, with faint counterparts in the optical or at 10
m, with faint counterparts in the optical or at 10![]() m.
m.