A&A 369, 677-689 (2001)
DOI: 10.1051/0004-6361:20010141
Observatoire de la Côte d'Azur, BP 4229, 06304 Nice Cedex 4, France
Received 19 October 2000 / Accepted 12 January 2001
Abstract
We re-derive the secular theory for Trojan-type motion from Morais
(1999) using a Hamiltonian formulation and show how this methodology
allows us to include the effect of an oblate central mass and the secular
perturbations from additional bodies in a rigorous way.
As an application of this work we locate secular resonances inside
the co-orbital regions of the uranian satellites and the planets, and show
that these are in good agreement with the behaviour observed in numerical
integrations.
Key words: celestial mechanics - minor planets, asteroids - planets and satellites: general
Lagrange (1867-1892) showed that the three-body problem has
five relative equilibrium configurations.
In the restricted version (i.e. when one of
the bodies is massless) it is useful to view the motion of the
test particle in a frame co-rotating with the massive bodies;
in this case the relative equilibrium configurations correspond
to fixed points two of which, named L4 and L5,
are linearly stable when the mass ratio is small enough (i.e. when
![]() ).
These are also known as the triangular equilibrium points and
correspond to configurations where the test particle is in the exact 1:1
mean motion resonance, i.e. it is co-orbital
).
These are also known as the triangular equilibrium points and
correspond to configurations where the test particle is in the exact 1:1
mean motion resonance, i.e. it is co-orbital![]() with m1 but leading
or trailing it by
with m1 but leading
or trailing it by
![]() .
In this paper, Trojan-type motion refers to the tadpole-shaped librations
around L4 or L5(in analogy with the Trojan asteroids which occupy tadpole orbits in the
Sun-Jupiter system) and also to the horseshoe-shaped librations that enclose
both triangular points
as well as the unstable co-linear point L3.
.
In this paper, Trojan-type motion refers to the tadpole-shaped librations
around L4 or L5(in analogy with the Trojan asteroids which occupy tadpole orbits in the
Sun-Jupiter system) and also to the horseshoe-shaped librations that enclose
both triangular points
as well as the unstable co-linear point L3.
In Morais (1999), hereafter Paper I, we constructed a secular theory for Trojan-type motion in the framework of the restricted three-body problem. A secular solution was derived based on the heuristic assumption that the terms in the averaged disturbing potential depending on the relative mean longitude do not have a net effect on the evolution of the eccentricity or inclination. Here we show how we can re-derive this secular solution applying first-order canonical adiabatic theory (Lichtenberg & Lieberman 1983). Moreover, we show that this methodology allows us to construct a complete secular theory which includes the effect of an oblate central mass and the secular perturbations from additional massive bodies, and we are thus able to explain rigorously some preliminary results obtained in Paper I.
Consider the hierarchical restricted three-body problem
with
![]() .
The equation that describes the motion in the vicinity of L4 or L5is
.
The equation that describes the motion in the vicinity of L4 or L5is
Note that the second term on the right hand side of Eq. (1)
vanishes at the triangular points; this means that a test particle located
at L4 (or L5) describes a keplerian ellipse which has an equal size,
equal shape and common focus to that described by the mass m1, but whose
orientation is shifted by
![]() (or
(or
![]() )
with respect to
the latter.
)
with respect to
the latter.
As usual we define the set (a, e, I, ![]() ,
,
![]() ,
,
![]() )
as the osculating elements (respectively, semi-major axis, eccentricity,
inclination, mean longitude, longitude of pericentre, longitude of node)
of the test particle's orbit.
Also, in our notation, unsubscribed quantities refer to
the test particle and
quantities with subscript k refer to a mass mk.
We then define the average angular velocity around the two-body
ellipse (or mean motion) as
)
as the osculating elements (respectively, semi-major axis, eccentricity,
inclination, mean longitude, longitude of pericentre, longitude of node)
of the test particle's orbit.
Also, in our notation, unsubscribed quantities refer to
the test particle and
quantities with subscript k refer to a mass mk.
We then define the average angular velocity around the two-body
ellipse (or mean motion) as
![]() ,
and we relate
this to the semi-major axis a by
,
and we relate
this to the semi-major axis a by![]()
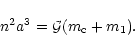 |
(3) |
| X | = | ||
| (5) |
Tadpole and horseshoe orbits can be decomposed into a slow guiding centre
motion described
by the variables
![]() and
and ![]() ,
with a superimposed fast
epicycle due to motion
from pericentre to apocentre viewed in the frame co-rotating with m1.
Averaging over the mean longitude
,
with a superimposed fast
epicycle due to motion
from pericentre to apocentre viewed in the frame co-rotating with m1.
Averaging over the mean longitude ![]() effectively removes the
epicyclic motion and
is justified in terms of perturbation theory by the fact that the amplitude
of the epicycle
is an adiabatic invariant. This is not only confirmed by numerical experiments
(e.g. Dermott & Murray 1981)
but has also been proved rigorously in the framework of Hill's problem
(Henon & Petit 1986).
Note, however, that the adiabatic invariance breaks down if the test particle
can get close to the mass m1.
Indeed, numerical experiments (Dermott & Murray 1981;
Gladman 1993)
show that near-circular and near-planar orbits with
effectively removes the
epicyclic motion and
is justified in terms of perturbation theory by the fact that the amplitude
of the epicycle
is an adiabatic invariant. This is not only confirmed by numerical experiments
(e.g. Dermott & Murray 1981)
but has also been proved rigorously in the framework of Hill's problem
(Henon & Petit 1986).
Note, however, that the adiabatic invariance breaks down if the test particle
can get close to the mass m1.
Indeed, numerical experiments (Dermott & Murray 1981;
Gladman 1993)
show that near-circular and near-planar orbits with
![]() (where
(where
![]() )
are strongly affected by successive
encounters with m1, thus being chaotic and potentially unstable.
The adiabatic invariance also breaks down in the vicinity of the separatrix
between the tadpole and horseshoe regions where there is overlap of high
order resonances between the angles
)
are strongly affected by successive
encounters with m1, thus being chaotic and potentially unstable.
The adiabatic invariance also breaks down in the vicinity of the separatrix
between the tadpole and horseshoe regions where there is overlap of high
order resonances between the angles ![]() and
and ![]() .
.
We now want to obtain the equation of the guiding centre (that gives
the evolution of ![]() with
with ![]() ).
From Lagrange's planetary equations we have
).
From Lagrange's planetary equations we have
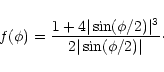 |
(10) |
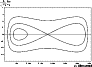 |
Figure 1:
Guiding centre trajectories obtained with Eq. (13):
-E=1.77465 (inner curves),
-E=2.50019 (separatrix) and
-E=4.08606(outer curve).
Note that |
| Open with DEXTER | |
Alternatively, we can describe the motion of the guiding centre using the
integrable Hamiltonian
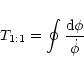 |
(16) |
| J | = | (17) | |
| = | (18) |
The time-independent Hamiltonian of the restricted three-body problem
can be written as
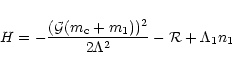 |
(19) |
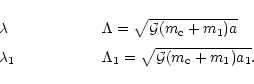 |
(20) |
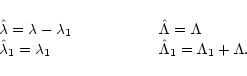 |
(21) |
It is straightforward to obtain again H0 (given by
Eq. (15)) by expanding Eq. (22)
in powers of
![]() ,
assuming that the eccentricities and the
inclinations are at most
,
assuming that the eccentricities and the
inclinations are at most
![]() ,
and
keeping only the terms up to
,
and
keeping only the terms up to
![]() while dropping
any constant terms.
We can then expand the Hamiltonian of the averaged
problem (Eq. (22)) to first-order
in the small parameter
while dropping
any constant terms.
We can then expand the Hamiltonian of the averaged
problem (Eq. (22)) to first-order
in the small parameter
![]() ,
i.e. we write
,
i.e. we write
Now suppose that the body with mass ![]() has an oblate shape with
equatorial
radius R and that we can consider only the dominant zonal harmonic term
(with coefficient J2) in the oblateness disturbing potential.
It can be shown (Kozai 1959) that the effect of the oblate planet
on a satellite's orbit
can be modeled by averaging the disturbing potential over the mean longitude,
i.e. by taking into account only
the secular part of the oblateness disturbing potential, which is
has an oblate shape with
equatorial
radius R and that we can consider only the dominant zonal harmonic term
(with coefficient J2) in the oblateness disturbing potential.
It can be shown (Kozai 1959) that the effect of the oblate planet
on a satellite's orbit
can be modeled by averaging the disturbing potential over the mean longitude,
i.e. by taking into account only
the secular part of the oblateness disturbing potential, which is
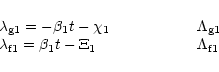 |
(33) |
Now consider N massive bodies orbiting a primary of mass ![]() .
It is well known (see e.g. Brouwer & Clemence 1961) that in the
absence of mean motion resonances between the N massive bodies, one can
obtain a good description of the long-term behaviour of, say mj,
by averaging the disturbing potential over the mean longitudes.
The expansion of this secular disturbing potential, up to
degree two in eccentricities and inclinations, is
.
It is well known (see e.g. Brouwer & Clemence 1961) that in the
absence of mean motion resonances between the N massive bodies, one can
obtain a good description of the long-term behaviour of, say mj,
by averaging the disturbing potential over the mean longitudes.
The expansion of this secular disturbing potential, up to
degree two in eccentricities and inclinations, is
The secular solution for the mass mj is simply
Moreover, the secular disturbing potential acting on a test particle in
a tadpole or horseshoe orbit associated with the mass mk,
due to the masses mj (where ![]() ), expanded up to degree two in
eccentricities and inclinations, is
), expanded up to degree two in
eccentricities and inclinations, is
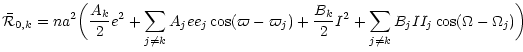 |
(37) |
We now want to see how the secular perturbations from these additional
massive bodies change the guiding centre's motion of tadpole or horseshoe orbits.
Obviously there are no secular perturbations to the semi-major axis.
Now, adding to the right hand side of Eq. (8) the contribution of the additional massive bodies to
![]() ,
yields
,
yields
Then, from Eqs. (38) and (9),
we obtain an integral of the ![]() -motion similar to Eq. (12).
Therefore, the motion of the guiding centre is still described by an integrable
Hamiltonian H0, which has the same form as Eq. (15).
So once more we write the Hamiltonian of the averaged problem as
-motion similar to Eq. (12).
Therefore, the motion of the guiding centre is still described by an integrable
Hamiltonian H0, which has the same form as Eq. (15).
So once more we write the Hamiltonian of the averaged problem as
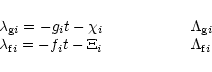 |
(41) |
We now recall Sect. 2.1.2 where we obtained the Hamiltonian of the averaged
problem (Eq. (23)) and then
apply Eq. (13) in order to write its first-order part
(Eq. (24)) as
| X | = | ||
| (43) |
By construction of the Hamiltonian of the averaged problem (Eq. (23))
the variables
![]() and
and
![]() vary on a timescale
vary on a timescale
![]() and therefore are much slower than
and therefore are much slower than
![]() ,
the angle variable of the integrable part H0.
The general procedure for dealing with this type of quasi-integrable systems
involves a canonical transformation of variables such that the new
Hamiltonian does not depend on the fast angle
and thus the associated action is an adiabatic invariant
(Lichtenberg & Lieberman 1983).
To first-order in the small parameter
,
the angle variable of the integrable part H0.
The general procedure for dealing with this type of quasi-integrable systems
involves a canonical transformation of variables such that the new
Hamiltonian does not depend on the fast angle
and thus the associated action is an adiabatic invariant
(Lichtenberg & Lieberman 1983).
To first-order in the small parameter
![]() ,
the transformed
Hamiltonian is
,
the transformed
Hamiltonian is
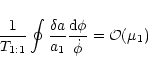 |
(47) |
| = | |||
| (49) |
 |
(50) |
![\begin{displaymath}g_i[l]=\frac{1}{T_{1:1}} \oint g_i(\phi) \frac{{\rm d}\, \phi}{\dot{\phi}}
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img143.gif) |
(51) |
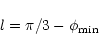 |
(52) |
From Paper I we recall that
![]() and
and
![]() ;
then we write
;
then we write![]()
| = | (53) | ||
| = | (54) | ||
| = | (55) | ||
| = | (56) |
![\begin{displaymath}a_0[l]=\sqrt{\frac{8}{3} \mu_1 \left( f(\pi/3-l)-\frac{3}{2} \right)}
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img158.gif) |
(57) |
We now write Hamilton's equations for (k,h) as
| = | 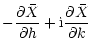 |
||
| = | (58) |
Similarly, we write Hamilton's equations for (q,p) as
| = | 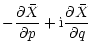 |
||
| = | (60) |
The Hamiltonian of the averaged problem has now six degrees of freedom
(cf. Sect. 2.2) i.e. two more than in the restricted three-body case.
However, we can eliminate these extra degrees of freedom
by making a canonical transformation to the following variables
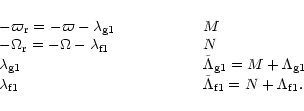 |
(62) |
| X | = | ||
| (64) |
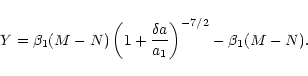 |
(65) |
The first term on the right hand side of Eq. (63)
can be dropped as there is no explicit dependence on
![]() or
or
![]() .
Hence, Eq. (63) has the same form as Eq. (42),
except for the term Y.
This introduces the relative precession frequencies
.
Hence, Eq. (63) has the same form as Eq. (42),
except for the term Y.
This introduces the relative precession frequencies
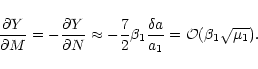 |
(66) |
| (67) |
| = | |||
| (68) |
![\begin{displaymath}\bar{Y}= \frac{1}{2} \Delta\bar{\beta}
[(h_{\rm r}^2+k_{\rm r}^2)-(p_{\rm r}^2+q_{\rm r}^2)]
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img194.gif) |
(69) |
 |
(70) |
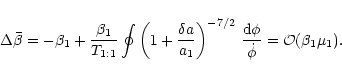 |
(71) |
Hamilton's equations for
![]() are
are
The Hamiltonian of the averaged problem has
![]() degrees of freedom
(cf. Sect. 2.3).
In order to reduce the number of degrees of freedom we perform a canonical
transformation to the following variables
degrees of freedom
(cf. Sect. 2.3).
In order to reduce the number of degrees of freedom we perform a canonical
transformation to the following variables
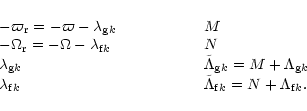 |
(76) |
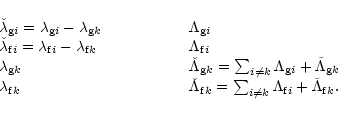 |
(77) |
| X | = | ||
| (79) |
| Y | = | (Ak-gk) M +(Bk-fk) N | |
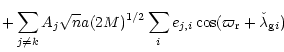 |
|||
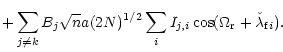 |
(80) |
We now assume
that the perturbers move on circular and co-planar orbits, in which
case the terms in Eq. (78) depending on
![]() and
and
![]() also disappear and the Hamiltonian reduces to
also disappear and the Hamiltonian reduces to
![\begin{displaymath}\bar{H}=H_0-(\gamma_k[l] +\bar{A}_k-g_k) M -(\Gamma_k[l]+\bar{B}_k-f_k) N
\end{displaymath}](/articles/aa/full/2001/14/aa10378/img235.gif) |
(82) |
| = |  |
(85) | |
| = | 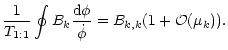 |
(86) |
We will now assume that not only the variables
![]() and
and
![]() but also the angles
but also the angles
![]() and
and
![]() vary on a time-scale much longer than the co-orbital period T1:1.
Note that while the first assumption will in general be true, the
same does not necessarily apply to the second assumption.
When the co-orbital frequency is comparable to one of the forcing
frequencies, a low order resonance can occur in which case the adiabatic
approximation does not provide a good description of the system.
Nevertheless, if we ignore this possibility then we can
apply Eqs. (45) and (46) to obtain the
transformed Hamiltonian
vary on a time-scale much longer than the co-orbital period T1:1.
Note that while the first assumption will in general be true, the
same does not necessarily apply to the second assumption.
When the co-orbital frequency is comparable to one of the forcing
frequencies, a low order resonance can occur in which case the adiabatic
approximation does not provide a good description of the system.
Nevertheless, if we ignore this possibility then we can
apply Eqs. (45) and (46) to obtain the
transformed Hamiltonian
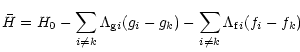 |
(89) |
| = | |||
| (90) |
| = | |||
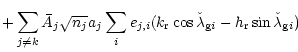 |
|||
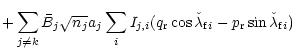 |
(91) |
| = | (92) | ||
| = | (93) |
| = | 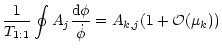 |
(94) | |
| = | 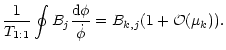 |
(95) |
The evolution of
![]() is described by
is described by
Note that although the secular solution obtained here
(Eqs. (97) and
(99)) has essentially the same form
as that obtained in Paper I, the terms ![]() and
and ![]() are
now defined as averages over T1:1 (which nonetheless
coincide, to lowest order, with the quantities defined in Paper I).
The basic improvement with respect to Paper I is the correct derivation of the
thresholds of validity of the secular solution which as we have seen now
simply depends on the validity of the adiabatic approximation.
are
now defined as averages over T1:1 (which nonetheless
coincide, to lowest order, with the quantities defined in Paper I).
The basic improvement with respect to Paper I is the correct derivation of the
thresholds of validity of the secular solution which as we have seen now
simply depends on the validity of the adiabatic approximation.
| i |
|
g1-gi | g2-gi | g3-gi | g4-gi | g5-gi |
| f1-fi | f2-fi | f3-fi | f4-fi | f5-fi | ||
| 1 | 1.1 10-2 | 0 | -7.0 10-4 | -8.5 10-4 | -9.1 10-4 | -9.7 10-4 |
| 0 | 7.0 10-4 | 8.5 10-4 | 9.1 10-4 | 9.7 10-4 | ||
| 2 | 2.9 10-2 | 7.0 10-4 | 0 | -1.5 10-4 | -2.1 10-4 | -2.7 10-4 |
| -7.0 10-4 | 0 | 1.5 10-4 | 2.1 10-4 | 2.8 10-4 | ||
| 3 | 1.3 10-2 | 8.5 10-4 | 1.5 10-4 | 0 | -6.0 10-5 | -1.2 10-4 |
| -8.5 10-4 | -1.5 10-4 | 0 | 5.4 10-5 | 1.2 10-4 | ||
| 4 | 1.1 10-2 | 9.1 10-4 | 2.1 10-4 | 6.0 10-5 | 0 | -6.1 10-5 |
| -9.0 10-4 | -2.1 10-4 | -5.4 10-5 | 0 | 6.9 10-5 | ||
| 5 | 7.0 10-3 | 9.7 10-4 | 2.7 10-4 | 1.2 10-4 | 6.1 10-5 | 0 |
| -9.7 10-4 | -2.8 10-4 | -1.2 10-4 | -6.9 10-5 | 0 |
We will now apply our secular theory to the case of Trojan orbits associated with the five major uranian satellites. As already noticed in Paper I, this system provides a good testing ground for our theory due to two reasons. First: there are no mean motion resonances amongst these satellites and thus the secular approximation (i.e. the average of the disturbing potential over the mean longitudes) is valid. Second: these satellites have nearly-circular and nearly-equatorial orbits thus satisfying the requirements of our secular theory.
We used the data from Malhotra et al. (1989) to
calculate the parameters of the secular theory for the uranian
system![]() and then identified the modes that satisfy
Eq. (87) (or Eq. (88)) inside the co-orbital
regions of its major satellites.
For instance, in order to locate secular resonances involving
the pericentres (or nodes) inside the co-orbital region of the mass mk, we
first plot
and then identified the modes that satisfy
Eq. (87) (or Eq. (88)) inside the co-orbital
regions of its major satellites.
For instance, in order to locate secular resonances involving
the pericentres (or nodes) inside the co-orbital region of the mass mk, we
first plot ![]() (or
(or ![]() )
)![]() as a function of a0 (a parameter that
characterizes the size of the tadpole or horseshoe orbit already defined in
Eq. (14)) and then identify the intersection with the
horizontal lines taken at
as a function of a0 (a parameter that
characterizes the size of the tadpole or horseshoe orbit already defined in
Eq. (14)) and then identify the intersection with the
horizontal lines taken at
![]() (or
(or
![]() ).
We show the location of the secular resonances
which occur inside the co-orbital regions of Miranda (m1), Ariel (m2),
Umbriel (m3), Titania (m4) and Oberon (m5) in Fig. 2.
Note that we can condense the results for the five satellites in
one single picture due to the fact that both
).
We show the location of the secular resonances
which occur inside the co-orbital regions of Miranda (m1), Ariel (m2),
Umbriel (m3), Titania (m4) and Oberon (m5) in Fig. 2.
Note that we can condense the results for the five satellites in
one single picture due to the fact that both ![]() and
and ![]() scale as
scale as ![]() (see also Paper I).
(see also Paper I).
We also used a Runge-Kutta-Nystron 12th order scheme (Brankin et al. 1987) to integrate the equations of motion of the system consisting of Uranus, its satellites and associated test particles in tadpole or horseshoe orbits. The parameters and initial conditions were again taken from Malhotra et al. (1989), and we incorporated an oblateness potential which takes into account only the dominant zonal harmonic.
In Paper I we showed the result of a numerical integration
for a test particle located near the L4 point of Titania (m4), which
included the gravitational interaction with Umbriel (m3) only.
We saw that in this
case the long-term behaviour of
![]() is affected by the
proximity of a secular resonance involving the mode g3 and is in
good agreement with the secular solution (Eq. (97)). In fact,
we can see from Table 1 that the adiabatic approximation made in Sect. 3.3.2
should be valid in the case of the uranian satellites, as the
co-orbital frequencies are much larger than the forcing frequencies.
is affected by the
proximity of a secular resonance involving the mode g3 and is in
good agreement with the secular solution (Eq. (97)). In fact,
we can see from Table 1 that the adiabatic approximation made in Sect. 3.3.2
should be valid in the case of the uranian satellites, as the
co-orbital frequencies are much larger than the forcing frequencies.
 |
Figure 2:
Location of secular resonances involving
a) the pericentres and b) the nodes, inside the co-orbital regions of
the uranian satellites Miranda (m1), Ariel (m2), Umbriel (m3),
Titania (m4) and Oberon (m5).
Secular resonances associated with the modes gi (or fi) occur
at the locations
|
| Open with DEXTER | |
In Fig. 3 we show the evolution of an orbit
located near the L4 point of Oberon with a0=0. This is very close
to the secular resonance involving the mode g4 (cf. Fig. 2)
and we see that the slow periodic motion of the critical argument
![]() is correlated with a large amplitude oscillation of the
eccentricity.
The small amplitude fast oscillation in the eccentricity has the same
periodicity as the argument
is correlated with a large amplitude oscillation of the
eccentricity.
The small amplitude fast oscillation in the eccentricity has the same
periodicity as the argument
![]() and is indeed
caused by the forced term due to the 1:1 mean motion resonance with
Oberon.
There is no apparent threat to the long-term stability of this orbit, as
the maximum eccentricity is still very far
from the threshold required for close approaches with nearby Titania
(i.e. e=0.25).
and is indeed
caused by the forced term due to the 1:1 mean motion resonance with
Oberon.
There is no apparent threat to the long-term stability of this orbit, as
the maximum eccentricity is still very far
from the threshold required for close approaches with nearby Titania
(i.e. e=0.25).
In Fig. 4 we show the evolution of a
horseshoe orbit associated with Oberon which has
![]() .
The eccentricity exhibits very irregular behaviour which is probably due to
the interaction between two nearby secular resonances (involving the modes
g3 and g4; cf. Fig. 2) as suggested by the
behaviour of the associated critical arguments. Due to the overlap
of the separatrices of these two secular resonances, the eccentricity diffuses
chaotically and can potentially reach stability-threatening values.
.
The eccentricity exhibits very irregular behaviour which is probably due to
the interaction between two nearby secular resonances (involving the modes
g3 and g4; cf. Fig. 2) as suggested by the
behaviour of the associated critical arguments. Due to the overlap
of the separatrices of these two secular resonances, the eccentricity diffuses
chaotically and can potentially reach stability-threatening values.
 |
Figure 3: Evolution of eccentricity (upper figure), critical arguments associated with the modes g4 (middle figure) and g5 (lower figure) for an orbit located near Oberon's L4 point with a0=0. Time is in units of Miranda's orbital period |
| Open with DEXTER | |
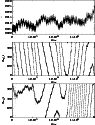 |
Figure 4:
Evolution of eccentricity (upper figure), critical arguments
associated with the modes g3 (middle figure) and g4 (lower figure)
for a horseshoe orbit associated with Oberon with
|
| Open with DEXTER | |
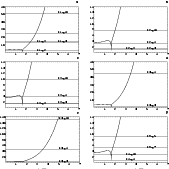 |
Figure 5:
Location of secular resonances involving the
pericentres inside the co-orbital regions of the planets.
The frequencies shown in the vertical axes are adimensional
and correspond to the true frequencies divided by |
| Open with DEXTER | |
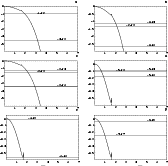 |
Figure 6:
Location of secular resonances involving the nodes
inside the co-orbital regions of the planets.
The frequencies shown in the vertical axes are adimensional
and correspond to the true frequencies divided by |
| Open with DEXTER | |
We remark here that although our secular theory cannot describe accurately the true behaviour in the very close vicinity of secular resonances (due to the occurrence of singularities in Eqs. (97) and (99) which is an artifact caused by the truncation of the disturbing potential at degree two in e and I) or whenever there is overlap of adjacent secular resonances (due to the underlying chaotic nature of the phase space), it is still very useful in the sense that it allows us to obtain the location of these secular resonances, whose dynamical effect can always be subsequently investigated with numerical integrations.
We also applied our secular theory to the system consisting of the eight
planets, Mercury to Neptune, using values for the eigen-frequencies of the
secular system from Brouwer & Van Woerkom (1950). As these
were calculated taking in account the effect of the 2:5 near
commensurability
between the orbital periods of Jupiter and Saturn, the secular
system is characterised by ten eigen-frequencies gi (with
g9=2 g5-g6 and
g10=2 g6-g5) and eight eigen-frequencies fi.
We then used these in order to obtain the locations of secular
resonances inside
the planetary co-orbital regions![]() condensed in the six panels of Figs. 5 and 6.
condensed in the six panels of Figs. 5 and 6.
Figure 5f proves that the secular resonances involving the modes g6 and g10 can affect Saturn's tadpole orbits which is in agreement with recent numerical integrations by Marzari & Scholl (2000). In particular, these latter authors suggest that the mixed secular resonance involving the mode g10 is the major factor responsible for the destabilization of tadpole orbits associated with Saturn. In Fig. 6b we see that the secular resonances involving the modes f3 and f4occur very close to each other inside Venus' horseshoe region, thus suggesting their possible overlap. In fact, the numerical integrations of Michel (1997) showed that a clone of asteroid (4660) Nereus becomes, at some stage in its life, a Venus' horseshoe orbit which exhibits chaotic diffusion of the inclination caused by the overlap of these two secular resonances.
From Fig. 6d and as already mentioned in Paper I, we see that the secular resonance involving the mode f6 occurs within Jupiter's tadpole region. Recent numerical integrations by Marzari & Scholl (2000) seem to support earlier suggestions by Yoder (1979) and Milani (1994) concerning the important role played by this secular resonance in the dynamical shaping of the Trojan cloud.
In this paper we were able to construct a complete linear secular theory for Trojan-type motion (i.e. based on expansions of the disturbing potential truncated at degree two in eccentricities and inclinations). This was achieved through the use of a Hamiltonian formulation which allowed us to generalise the theory presented in Paper I by including, in a rigorous way, the effect of an oblate central mass and the secular perturbations from additional massive bodies.
Using our theory we were able to locate secular resonances inside the co-orbital regions of the uranian satellites and the planets Mercury to Neptune. Comparison with numerical integrations showed that these locations are reasonably accurate and that secular resonances seem to play a major role in determining the stability of Trojan orbits.
We end by remarking that a next necessary step would be to develop a non-linear secular theory. In particular this would allow us to obtain even more accurate locations for these secular resonances (i.e. as functions of not only the proper semi-major axis, but also the proper eccentricity and the proper inclination). Moreover, a non-linear secular theory is also essential for application to the co-orbital structures with high eccentricity and/or inclination, studied by Namouni (1999).
Acknowledgements
I thank A. Morbidelli, D. Nesvorny and the reviewer, D. Hamilton, for useful comments. This work was supported by grants PRAXIS XXI/BD/5072/95 and SFRH/BPD/1586/2000 from the Fundação para a Ciência e a Tecnologia, Portugal.