Cosmic ray nuclei can be broken up in collisions with thermal matter; this
process is called spallation. Obviously, there is a corresponding
interaction between energetic protons, and thermal material comprising
heavier nuclei such as carbon. In such collisions the remaining nuclei
can also be excited, and then emit ![]() -ray lines.
-ray lines.
Spallation is relevant in various sites (see, e.g., the recent
work in this area, Garcia-Munoz et al.![]() 1977; Engelmann et al.
1977; Engelmann et al.![]() 1985; Garcia-Munoz et al.
1985; Garcia-Munoz et al.![]() 1987; Engelmann et al.
1987; Engelmann et al.![]() 1990; Shibata 1996 and the classical reviews by Reeves 1974, 1994). The site normally explored is interstellar
clouds Spitzer (1968); cosmic rays travel through the interstellar medium, and interact. Good evidence for this interaction is the excellent correlation of the observed
gamma ray continuum emission (arising from
1990; Shibata 1996 and the classical reviews by Reeves 1974, 1994). The site normally explored is interstellar
clouds Spitzer (1968); cosmic rays travel through the interstellar medium, and interact. Good evidence for this interaction is the excellent correlation of the observed
gamma ray continuum emission (arising from ![]() decay following p-p
interaction) with the observed column density of interstellar material
(Hunter et al.
decay following p-p
interaction) with the observed column density of interstellar material
(Hunter et al.![]() 1997).
1997).
Massive stars eject all the material enriched over the big bang
nucleosyntheis into the interstellar medium. Massive stars are also
believed to be the sources of energetic particles; massive stars have powerful winds,
which sweep up interstellar matter. Massive stars have so much mass
loss, that they shed their outer layers, expose the processed material and thus
late in life show a highly enriched wind. The wind, on the other hand, plows into the
environmental gas, and sweeps it up; gas left over from the formation
of the star may still be around as well, so as to increase the target for the expanding
wind and form a shell. It is through this enriched wind and associated shell,
that the supernova shock races, and causes particle acceleration and
spallation by these particles directly. We note that the supernova shock
compresses the wind itself into a shocked shell, which then smashes into the shell
produced by the progenitor stellar wind. As the previous wind was also
already enriched, spallation necessarily occurs in an enriched environment:
such an enrichment is actually required by the light element data of old
stars as shown by Ramaty et al.![]() (1997), but would of course also be consistent with other
scenarios than the one introduced here (the dust model mentioned below).
(1997), but would of course also be consistent with other
scenarios than the one introduced here (the dust model mentioned below).
We note that the evolution of massive stars can now be modelled
including the effects of rotation, the induced mixing and the strong winds
(Heger & Langer 1998; Langer et al.![]() 1999); the mixing of the chemical element
composition throughout the star during the evolution fixes the abundances in the
wind, the site of acceleration upon explosion as a supernova. For the
proposal as to the origin of cosmic rays it is a necessary ingredient, that these
stars have fairly substantial magnetic fields (Thum & Morris 1999; Seemann & Biermann 1997).
1999); the mixing of the chemical element
composition throughout the star during the evolution fixes the abundances in the
wind, the site of acceleration upon explosion as a supernova. For the
proposal as to the origin of cosmic rays it is a necessary ingredient, that these
stars have fairly substantial magnetic fields (Thum & Morris 1999; Seemann & Biermann 1997).
Stars along the main sequence need to be considered in four separate zero age mass ranges:
Therefore we can ask the following question: what happens when the supernova shock smashes into the wind-driven shell? The supernova shock shell is loaded with cosmic ray particles. In the enriched shock shell and wind shell the energetic particles may reside for some time, and then leak out into the normal interstellar medium. What is the wavefield that governs this leakage in the limit that the leakage is diffusive?
Therefore, we need to consider the diffusive loss from a shell, which is traversed by a shock filled with a cosmic ray population. So we first derive the wavefield in magnetic fields excited by the cosmic rays. Then, in a second step we consider the diffusive leakage from the shell under the influence of this wave field.
Turbulence is an ubiquitous phenomenon, and also is a key ingredient in the
interstellar medium (see reviews by Rickett 1990; Goldstein et al.![]() 1995). Key
concepts to turbulence theory have been introduced by Prandtl (1925), Karman & Howarth (1938), Kolmogorov (1941a, 1941b, 1941c),
Obukhov (1941), Heisenberg (1948), Kraichnan (1965),
and have been reviewed by Sagdeev (1979). One key argument
which we wish to use, is the concept of the turbulent cascade. In a cascade
the energy of the turbulence is injected into the gas at some large
wavelength, and cascades down through wavenumber space, to the small
wavelengths where the energy is dissipated; in many examples this
leads in a three-dimensional isotropic model to the Kolmogorov cascade
(Matthaeus & Zhou 1989), which can be described in a local approximation by the following diffusion equation in wavenumber space (McIvor 1977; Achterberg 1979).
1995). Key
concepts to turbulence theory have been introduced by Prandtl (1925), Karman & Howarth (1938), Kolmogorov (1941a, 1941b, 1941c),
Obukhov (1941), Heisenberg (1948), Kraichnan (1965),
and have been reviewed by Sagdeev (1979). One key argument
which we wish to use, is the concept of the turbulent cascade. In a cascade
the energy of the turbulence is injected into the gas at some large
wavelength, and cascades down through wavenumber space, to the small
wavelengths where the energy is dissipated; in many examples this
leads in a three-dimensional isotropic model to the Kolmogorov cascade
(Matthaeus & Zhou 1989), which can be described in a local approximation by the following diffusion equation in wavenumber space (McIvor 1977; Achterberg 1979).
The basic concept here is as follows: cosmic rays excite turbulence at all
wavelengths through resonance, with the wavenumber
![]() ,
where
,
where ![]() is the Larmor radius of a cosmic ray particle in the magnetic
field. The entire spectrum of cosmic rays excites turbulence. This excitation takes
place in the region near to and upstream from the super-nova shock, where there
is a spatial gradient in cosmic ray flux. Downstream from the shock, where
there is no more spatial gradient in the cosmic ray flux, the turbulence
spectrum is given, and stays constant. A competing process to excitation is
cascading, and the following equations describe this competition, with the first one showing
cascading by itself:
is the Larmor radius of a cosmic ray particle in the magnetic
field. The entire spectrum of cosmic rays excites turbulence. This excitation takes
place in the region near to and upstream from the super-nova shock, where there
is a spatial gradient in cosmic ray flux. Downstream from the shock, where
there is no more spatial gradient in the cosmic ray flux, the turbulence
spectrum is given, and stays constant. A competing process to excitation is
cascading, and the following equations describe this competition, with the first one showing
cascading by itself:
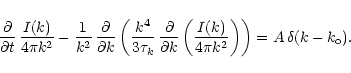 |
(1) |
Here I(k) is the energy density of the turbulence per wavenumber k,
and per volume element, and ![]() is the time scale of diffusion, which
can be written as
is the time scale of diffusion, which
can be written as
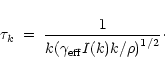 |
(2) |
Here ![]() is the matter density, and
is the matter density, and
![]() is an effective
adiabatic constant for the turbulent energy. The turbulence has a
source-term, here limited to a single wavenumber ko. Below we will
consider an entire range of excitation wave numbers. The turbulence
diffusion equation basically says that the turbulence moves through
wavenumber space with no additional source or sink, as a constant energy
current in wavenumber phase space
(Kolmogorov 1941a; Kolmogorov 1941b; Kolmogorov 1941c). The solutions to this diffusion equation can be written as
is an effective
adiabatic constant for the turbulent energy. The turbulence has a
source-term, here limited to a single wavenumber ko. Below we will
consider an entire range of excitation wave numbers. The turbulence
diffusion equation basically says that the turbulence moves through
wavenumber space with no additional source or sink, as a constant energy
current in wavenumber phase space
(Kolmogorov 1941a; Kolmogorov 1941b; Kolmogorov 1941c). The solutions to this diffusion equation can be written as
![]() and
and
![]() .
This latter behaviour is commonly referred to as the Kolmogorov cascade,
and is found ubiquitously in nature.
.
This latter behaviour is commonly referred to as the Kolmogorov cascade,
and is found ubiquitously in nature.
The basic equation for the excitation of wavefields can be written as
follows (Bell 1978a; Drury 1983):
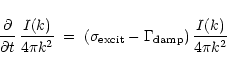 |
(3) |
with
![]() the excitation term and
the excitation term and
![]() the damping term. Here we will concentrate on the excitation of waves, and
ignore any damping. The excitation term can be written as
the damping term. Here we will concentrate on the excitation of waves, and
ignore any damping. The excitation term can be written as
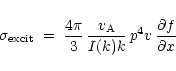 |
(4) |
where v is the particle velocity, f the particle distribution function in phase space (assumed to be isotropic), and x the local coordinate perpendicular to the shock plane. We need to emphasize that only the difference of the particle spectrum across a shock wave or any other spatial gradient can excite waves; therefore, the first shock wave loaded with cosmic ray particles sweeping across the molecular gas shell around exploding stars and their winds is the excitation mechanism, which we consider. Now the particle spectrum in energy space (in the relativistic domain of particle speeds) is N(E) = E-7/3 from the arguments of shocks in winds (Biermann 1993a; Biermann & Cassinelli 1993). Of course, this step in the argument depends on the proposal for the origin of cosmic rays summarized earlier to be correct. This earlier argument entails that the length scale inherent in the upstream gradient of cosmic rays is independent of energy, different in this subtle point from Bell (1978a). We defer the combined solution of the cascade equations and the cosmic ray kinetic equations to later work, since for such an endeavour the highly turbulent shock region needs to be modelled in much more detail than possible at this stage.
We therefore need to determine which wave spectrum can balance the cascading
with the excitation from the freshly injected cosmic rays. Equating the
two expressions above for the cascading (Eq. (1)) and the excitation (Eq. (3))
in their k-dependence using an arbitrary powerlaw for
![]() then yields the condition
then yields the condition
![]() which means
which means
![]() .
We omit here for lack of space a thorough
discussion of the errors in this line of argument, as in e.g.
(Biermann & Cassinelli 1993; Biermann 1997a; Wiebel-Sooth et al.
.
We omit here for lack of space a thorough
discussion of the errors in this line of argument, as in e.g.
(Biermann & Cassinelli 1993; Biermann 1997a; Wiebel-Sooth et al.![]() 1998). From (Drury 1983) we obtain the diffusion
coefficient based on the wavefield, and then the diffusive time scale
of loss from the diffusion coefficient in turn.
1998). From (Drury 1983) we obtain the diffusion
coefficient based on the wavefield, and then the diffusive time scale
of loss from the diffusion coefficient in turn.
To emphasize the argument here: the spatial gradient near to and upstream of the supernova shock excites turbulence at all wavelengths through resonance between waves and the Larmor motion of cosmic ray particles; the turbulent spectrum is established by competition between excitation and cascading. In the downstream region then the turbulent spectrum is given, stays constant, and determines the post-shock leakage of cosmic rays from the region.
The diffusion coefficient in the quasilinear appproximation is given by
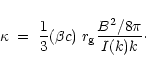 |
(5) |
This entails an energy dependence of the leakage time from the zone of
interaction
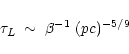 |
(6) |
for
![]() where
where
![]() is the momentum of the
particle multiplied with the speed of light, so the energy in the relativistic
limit. However, in order to allow a discussion also below relativistic energies,
we use here the trans-relativistic description, which requires the
momentum. This then means that the local spectrum of primary cosmic rays is
steeper by this much, and so all secondaries are produced with a spectrum which is
steeper by this much from the start.
is the momentum of the
particle multiplied with the speed of light, so the energy in the relativistic
limit. However, in order to allow a discussion also below relativistic energies,
we use here the trans-relativistic description, which requires the
momentum. This then means that the local spectrum of primary cosmic rays is
steeper by this much, and so all secondaries are produced with a spectrum which is
steeper by this much from the start.
![]() is a critical momentum, below which the convective break up
induced by the shock takes over, and the time scale becomes independent of
particle momentum. There is also an upper limit for the validity of the
diffusion approximation,
is a critical momentum, below which the convective break up
induced by the shock takes over, and the time scale becomes independent of
particle momentum. There is also an upper limit for the validity of the
diffusion approximation,
![]() ,
where the diffusion time becomes
equal to the travel time of particles at the speed of light through the
region of interaction. Beyond that limit again, the interaction time becomes a constant
with energy. So, the diffusion approximation has both lower and upper limits
for the transrelativistic momentum. Outside these limits the
interaction time is constant with particle energy. The momentum (or "rigidity") range
between these two limits should therefore be of order 10 to 30. Obviously, at
,
where the diffusion time becomes
equal to the travel time of particles at the speed of light through the
region of interaction. Beyond that limit again, the interaction time becomes a constant
with energy. So, the diffusion approximation has both lower and upper limits
for the transrelativistic momentum. Outside these limits the
interaction time is constant with particle energy. The momentum (or "rigidity") range
between these two limits should therefore be of order 10 to 30. Obviously, at
![]() and at
and at
![]() the time scale has to be continuous.
the time scale has to be continuous.
The grammage traversed then is given by the product of this time scale multiplied
with the average density in the interaction region, and also multiplied
with the particle velocity:
| (7) |
cancelling one ![]() -dependence. Thus, in the (zero age)
mass range of stars considered here, above 25 solar masses, the grammage traversed
as a function of energy is first proportional to
-dependence. Thus, in the (zero age)
mass range of stars considered here, above 25 solar masses, the grammage traversed
as a function of energy is first proportional to ![]() ,
then p-5/9,
and finally merges into a constant.
,
then p-5/9,
and finally merges into a constant.
The grammage can be estimated from the observed boron/carbon (B/C) ratio in the CR-data using the point where the E-0.6 breaks down, and the B/C ratio becomes consistent with a constant for higher energies. Integrating through a stellar wind of a WR-star and through the wind-driven shell to get the total interacting material one indeed obtains a grammage consistent with the requirements from the data, of order 10 gm/cm2, as required by the data.
Therefore, within the energy range of validity of the diffusion
approximation, secondaries are produced with a spectrum of
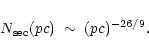 |
(8) |
For the stars between about 15 and 25 solar masses, we have a thin non-diffusive shell, where the escape time is just proportional to the inverse particle velocity
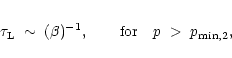
or again, if the general convective velocities are larger than
the particle velocity, then the leakage time from the shell becomes independent
of particle energy for
![]() (the index "2" is here
to make obvious that this minimum momentum may be different in the two stellar mass
ranges). Thus, in the (zero age) mass range of stars considered here,
between 15 and 25 solar masses, the grammage traversed as a function of energy is first
proportional to
(the index "2" is here
to make obvious that this minimum momentum may be different in the two stellar mass
ranges). Thus, in the (zero age) mass range of stars considered here,
between 15 and 25 solar masses, the grammage traversed as a function of energy is first
proportional to ![]() ,
and then becomes a constant.
,
and then becomes a constant.
Considering again the CR-data for the C/B ratio as a function of energy, we note that the stars in this mass range do not contribute any significant new carbon from their wind, just the carbon already present in the original gas from which the star formed.
After transport through the Galaxy and
insignificant further spallation this means that the ratio of
secondaries to primaries remains at
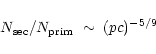 |
(9) |
which is rather close to the observed dependence from the
boron to carbon ratio of E-0.6 (Engelmann et al.![]() 1990).
1990).
Clearly, as expounded above, this treatment breaks down at two ends, both on the low energy side, and on the high energy side. On the high energy side, it is obvious that from some energy the diffusive approximation breaks down, and from the low energy end it is clear that convective losses and the full break up of the shell will be faster than diffusion below some energy.
There is necessarily also some interaction during the wandering through the interstellar medium (ISM): this interaction can be estimated by observing that the cosmic ray disk is at least 2 kpc thick in full width, while the cold gas disk is about 100 pc only. The average density in the cold gas disk is about 1 particle per cc, and so the average density as seen by the cosmic rays is about 0.05 per cc, and so of interest only at high energy. This interaction is governed by the Kolmogorov spectrum, and so those secondaries should be steeper than the primaries by 1/3 in spectrum. The total grammage traversed through the ISM by particles near GeV can thus be estimated as near 2.5 gm/cm2.
The picture presented in the earlier sections of this paper, however, is in
contrast to the usual finding that a stationary leaky box gives a
ratio of secondary to primaries ![]() (pc)-1/3, if we use a Kolmogorov
spectrum for turbulence; this latter result is obtained, when the interaction happens evenly
throughout the residence period in the Galaxy.
(pc)-1/3, if we use a Kolmogorov
spectrum for turbulence; this latter result is obtained, when the interaction happens evenly
throughout the residence period in the Galaxy.
This is also in contrast to the concept of clouds capturing and then releasing cosmic ray particles derived in (Biermann 1996).
Therefore, the effective interaction path is the sum of the composite shell interaction and the ISM, in some cases for the stars above 25 solar masses, and in some cases for the stars between 15 and 25 solar masses, while for the stars between about 8 and 15 solar masses the interstellar medium dominates.
The cosmic rays observed are the sum of the various CR-populations arising from explosions of stars in the three mass ranges considered here separately.
Therefore, considering the history of the travel of cosmic rays through
the normal interstellar medium (see also, e.g.
Biermann 1996; Pohl et al.![]() 1997), we can readily explain the ratio of secondaries to primaries, and at the same time use a spectrum of turbulence which is
consistent with all other observational evidence. Translating this
result into the language common in the literature, this means that
interaction path as measured in gm/cm2 and escape time can not be used
synonymously. The escape time is given by
1997), we can readily explain the ratio of secondaries to primaries, and at the same time use a spectrum of turbulence which is
consistent with all other observational evidence. Translating this
result into the language common in the literature, this means that
interaction path as measured in gm/cm2 and escape time can not be used
synonymously. The escape time is given by
![]() ,
and is
proportional to E-1/3 in the relativistic range of particle
energies. The interaction path as a means to describe interaction is
here
,
and is
proportional to E-1/3 in the relativistic range of particle
energies. The interaction path as a means to describe interaction is
here ![]() (pc)-5/9 gm/cm2. The real time corresponding to the interaction
phase is surely very short compared to the leakage time scale.
(pc)-5/9 gm/cm2. The real time corresponding to the interaction
phase is surely very short compared to the leakage time scale.
Copyright ESO 2001