

Up: On the duration of
According to the picture presented by Davies & Pringle the
magnetosphere of the neutron star in the state of subsonic propeller
is surrounded by the adiabatic (
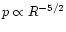 )
spherically
symmetrical plasma envelope. Until the energy input to the envelope
dominates the energy losses the temperature of the envelope plasma is
of the order of the free-fall temperature,
)
spherically
symmetrical plasma envelope. Until the energy input to the envelope
dominates the energy losses the temperature of the envelope plasma is
of the order of the free-fall temperature,
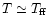 and,
correspondingly, the sound speed is of the order of the free-fall
velocity,
and,
correspondingly, the sound speed is of the order of the free-fall
velocity,
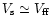 .
Under this condition the
height of the homogeneous atmosphere through out the envelope is
comparable to R and thus, the envelope is extended from the
magnetospheric radius,
.
Under this condition the
height of the homogeneous atmosphere through out the envelope is
comparable to R and thus, the envelope is extended from the
magnetospheric radius,
up to the accretion radius of the neutron star,
Here, V8 is the relative velocity between the neutron star
and the stellar wind plasma,
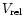 ,
expressed in units of
,
expressed in units of
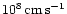 and
and 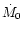 is strength of the stellar
wind which is expressed following DP81 in terms of
the maximum possible accretion rate:
is strength of the stellar
wind which is expressed following DP81 in terms of
the maximum possible accretion rate:
where
 is the density of the stellar wind plasma.
Within the considered picture the envelope is quasi-static, i.e.
the mass flux through the envelope is almost zero. In this situation
the physical meaning of the parameter
is the density of the stellar wind plasma.
Within the considered picture the envelope is quasi-static, i.e.
the mass flux through the envelope is almost zero. In this situation
the physical meaning of the parameter 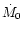 is the rate by
which the stellar wind plasma overflows the outer edge of the envelope
compressing the envelope plasma.
is the rate by
which the stellar wind plasma overflows the outer edge of the envelope
compressing the envelope plasma.
The interaction between the fast rotating magnetosphere and the base
of the envelope leads to the turbulization of the envelope plasma.
The velocity of the convection motions at the magnetospheric
boundary is obviously limited as
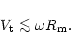 |
(4) |
Under the condition
 the maximum velocity of the
convective motions is smaller than
the maximum velocity of the
convective motions is smaller than 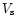 and hence, the Mach
number at the base of the envelope is
and hence, the Mach
number at the base of the envelope is
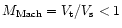 .
.
The rate of energy loss by the neutron star and, correspondingly,
the energy input to the envelope in this case can be expressed as (see
Eqs. (3.2.1) and (3.2.2) in DP81)
As it has been argued by Davies & Pringle the cooling of the
envelope plasma is determined by the combination of convective
motions and bremsstralung radiation. In order to evaluate the
energy balance between the heating and cooling processes they
introduced the convective efficiency parameter (see also Cox & Guili
1968):
Under the conditions of interest this parameter can be expressed as
(for discussion see DP81, p. 221)
![\begin{displaymath}\Gamma = M_{\rm Mach}^2 \left[\frac{V_{\rm t} t_{\rm br}}{R}\right] =
\frac{V_{\rm t}^3 t_{\rm br}}{V_{\rm s}^2 R},
\end{displaymath}](/articles/aa/full/2001/11/aada024/img40.gif) |
(5) |
where
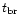 is the bremsstralung cooling time:
is the bremsstralung cooling time:
![\begin{displaymath}t_{\rm br} = 6.3 ~ 10^4
\left[\frac{T}{10^9\,{\rm K}}\right]^...
...}
\left[\frac{n}{10^{11}\,{\rm cm^{-3}}}\right]^{-1} {\rm s}.
\end{displaymath}](/articles/aa/full/2001/11/aada024/img42.gif) |
(6) |
Here, n is the number density of the envelope plasma which at the
base of the envelope can be evaluated as
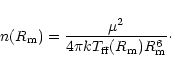 |
(7) |
As it has been shown in DP81 the cooling of the envelope
during the subsonic propeller state occurs first at its inner radius.
Thus, the energy input to the envelope due to the neutron star
propeller action dominates the radiative losses if
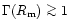 .
.
Combining Eqs. (1-7) I find the condition
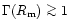 to be satisfied if the spin period of the neutron
star is
to be satisfied if the spin period of the neutron
star is
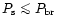 ,
where the break period is
,
where the break period is
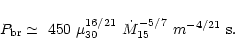 |
(8) |
This value of the break period exceeds the value of
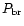 presented in DP81 by a factor of 7.5 (see Eq. (4.8)
in DP81). Hence the natural question about the reason of this
inconsistency arises. One of the most possible reasons is that Davies
& Pringle have mistakenly used the value of the magnetospheric
radius:
presented in DP81 by a factor of 7.5 (see Eq. (4.8)
in DP81). Hence the natural question about the reason of this
inconsistency arises. One of the most possible reasons is that Davies
& Pringle have mistakenly used the value of the magnetospheric
radius:
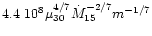 cm (see Eq. (3.2.3) of their paper) instead of the correct
value which is expressed in their paper by Eq. (2.5), i.e.
cm (see Eq. (3.2.3) of their paper) instead of the correct
value which is expressed in their paper by Eq. (2.5), i.e.
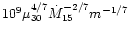 cm. Taking into account
that
cm. Taking into account
that
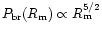 one finds that the correct
value of
one finds that the correct
value of
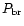 should be larger than that derived in DP81 by a
factor of 7.7, i.e. very close to the value of the break period
obtained in this letter.
should be larger than that derived in DP81 by a
factor of 7.7, i.e. very close to the value of the break period
obtained in this letter.


Up: On the duration of
Copyright ESO 2001
![]() )
spherically
symmetrical plasma envelope. Until the energy input to the envelope
dominates the energy losses the temperature of the envelope plasma is
of the order of the free-fall temperature,
)
spherically
symmetrical plasma envelope. Until the energy input to the envelope
dominates the energy losses the temperature of the envelope plasma is
of the order of the free-fall temperature,
![]() and,
correspondingly, the sound speed is of the order of the free-fall
velocity,
and,
correspondingly, the sound speed is of the order of the free-fall
velocity,
![]() .
Under this condition the
height of the homogeneous atmosphere through out the envelope is
comparable to R and thus, the envelope is extended from the
magnetospheric radius,
.
Under this condition the
height of the homogeneous atmosphere through out the envelope is
comparable to R and thus, the envelope is extended from the
magnetospheric radius,
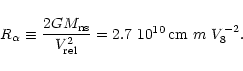
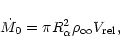
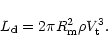

![]() to be satisfied if the spin period of the neutron
star is
to be satisfied if the spin period of the neutron
star is
![]() ,
where the break period is
,
where the break period is